Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Сибирская государственная автомобильно-дорожная академия

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

2017.pdf

Скачиваний:

Добавлен:

07.01.2021

Размер:

2.61 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 56 / 186 7 8 9 10 11 12 13 14 15 16 17 18 > Следующая >>>

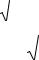
Пример 7. Исследовать на сходимость ряд

n 1

Решение. Имеем

n 1

5n 1

lim

n an

10 n

10 n 1

5n 1 10 n 2 20

5 n 2

lim

n 1

10 n

2 20

С20

lim5

5 lim

5 120

5 1,

следовательно, по

Даламбера

признаку

ряд расходится.

Без доказательства сформулируем признак Коши, который целе-

сообразно использовать, когда

является степенью некоторого вы-

n 1

ражения, например an

, или an

Дn

§6. Признак сходимости Коши

Сравнение рядов с прогрессиями приводит ещё и к другому при-

знаку сходимости, принадлежащему Коши.

Теорема 1 (признак Коши). Пусть ряд (1.19) с неотрицательны-

ми членами. Допустим, что

lim

существует и

limn

(1.22)

Тогда:

если 1, то ряд (1.19) сходится;

если 1, то ряд (1.19) расходится; если 1, то ряд (1.19) может быть как сходящийся, так и рас-

ходящийся (см. приведенные ниже примеры 4 и 5) [6].

Пример 1. Исследовать на сходимость ряд

3n 2

n 1 3n 2

Решение. Имеем

, следо-

lim n an

lim n

lim

3n 2

n 3n 2

Коши

вательно, по пр знаку

ряд сходится.

Пр мер 2. Исследовать на сходимость ряд

n 1 n2

3 4

n 1 n2

бА

n 1

Решен е. Напомн м, что lim 1

e 2,7. Имеем

n 1

lim

1 n

e 1,

следовательно,

по признаку Коши ряд расходит-

lim 1

ся.

Пример 3. Исследовать на сходимость ряд

n2 2n

8 16

n2 2n

n 2

49Д

Решение. Имеем

lim

Иn 2n

lim

n2 2nlim

n 3n2 1

		1	2		n
n							1	n
				n					0 1,
	lim					lim
							3
	n			1		n
		3
			n2

следовательно, по признаку Коши ряд сходится.
		Пример 4. Исследовать на сходимость ряд
							1 n					1									1				2							1		n
				1					1								1												1						.
				1					1			1					1				2								1				n		.
			n 1				n					1									2												n
		Решение. Имеем

																					1			n								1
					lim n an																1			n								1			1.
											lim n						1									lim			1
											lim n						1					n				lim			1			n
					n						n											n				n						n
	ходимое
		ледовательно, по признаку Коши данный ряд исследовать
С																											1 n
нельзя. другой стороны, lim an																			lim 1												e 0, следовательно,
											n									n							n
			бА
не выполняется нео															условие сходимости ряда, значит, дан-
ный ряд расход тся.
		Пр мер 5. Исследовать на сходимость ряд
									1						1				1								1			.
											1																n2			.
								n 1n2						2		2			32								n2
		Решение. Используя равенство lim 1, получаем
																							0
																				1		2
																				1		2
									1									1	n
									1									1	n
																			Д
		lim n an			limn					2	lim							n							12		1,				но этот ряд сходится,
		n			n				n	2	n							n
									n

так как если отбросить первых два члена, то он совпадает с рядом
1		1				1												1						, который является сходящимся


32		42			n 2 2								n 1 n 2 2															И
32		42			n 2 2								n 1 n 2 2

(см. пример 2 §5).

§7. Интегральный признак сходимости

Как видно из доказательства признака Даламбера, а признак Коши доказывают аналогично, эти два признака дают ответ о сходимости только тех рядов, порядок малости членов которых не меньше, чем у ряда геометрической прогрессии, т.е. только для быстро сходящихся рядов. С другой стороны, эти признаки устанавливают расходимость только таких рядов, у которых общий член даже не стремится к нулю. Эти признаки, следовательно, являются слишком грубыми.

Они неприменимы к рядам с медленно растущими частичными суммами, каким является, например, гармонический ряд.

формулируем сейчас признак, который в некоторой степени восполняет этот пробел.

Теорема 1 (интегральный признак). Пусть дан ряд (1.19) с по-

ложительными членами, причем a1 a2

и f n та-

кая непрерывная монотонно убывающая функция,

что f n an . То-

гда данный

ряд

несобственный

интеграл

f x dxодновременно

ский

сходится

ли расход тся.

СПр мер 1. Исследовать на сходимость обобщенный гармониче-

ряд

бА

0, 1.

n 1

Решен е. Рассмотрим функцию f x

, x 1. Эта функция

непрерывна,

монотонно у ывает и

f n

следовательно, можно

применить интегральный признак. При 1 имеем

M dx

lim

M 1 x

M 1

lim

M1 11

lim M1 1 .

1 M

Здесь необходимо рассмотреть два случая:

1 0,

т.е.

или 1 0

;

следовательно,

стремится к нулю,

если M стремится к бесконечности.

Тогда

lim

1 x

1 M M 1

таким образом, при 1 данный ряд сходится.

частности,

ряд

сходится, т.к.

1 0,

т.е. 1.

Тогда

неограниченно возрастает при M ,

стремящемся к бесконечности, следовательно,

lim M1 1

1 x

1 M

и данный ряд расходится.

B частности, ряд 1

расходится, так как

3 2

3 3

3 n

Рассмотрим

Пр мер 2. Исследовать на сходимость ряд

ln3 n 2

ln3 3

ln3

4 ln3 5

ln3 n 2

убывает

n 2

n 1

n 2

f x

ln3 x 2

Решен е.

функцию

x 2

, x 1. Эта

функция непрерывна,

монотонно

f n

ln3 n 2

, следо-

n 2

вательно,

можно

применить

интегральный

признак

ln3 x 2

M ln3 x 2

dx lim

x 2

M 1

ln4 x 2 M

lim

x 2 d lnАx 2 lim

M 1

lim

ln4 M 2 ln4

3 ,

M 4

т.к.ln4(M 2) неограниченно возрастаетДпри M , стремящемся к бес-

конечности. Следовательно, ряд расходится.

Пример 3. Исследовать на сходимость ряд

n 1e

e И

Решение. Рассмотрим функцию f x

, x 1. Эта функция

непрерывна, монотонно убывает и

, следовательно, можно

применить интегральный признак

2x dx

dx lim

xdx

lim

1 ex2

M 1

lim e

lim

2M eM

.к. eM 2

неогран ченно возрастает при M ,

стремящемся к бесконеч-

. Следовательно, данный ряд сходится по интегральному при-

ности

знаку.

Вывод. Интегральный признак Коши является, как видно из его

формулировки, нео ходимым и достаточным признаком. Это значит,

что он устанавливает сходимость

сходящегося ряда и расхо-

любого

димость любого расходящегося ряда из сферы своей применимости.

Иными словами, интегральный признак является идеально чувстви-

А тельным. В этом отношении онДнапоминает критерий сходимости

Коши. Естественно, что все такие «необходимые и достаточные» признаки, если только они сколько-нибудь широки, неизбежно оказываются по отношению ко многим рядам непрактичными. В этом можно усмотреть проявление весьма общей закономерности: чем шире и богаче возможности того или иного математическогоИаппарата, тем сложнее его логическая природа и тем труднее с ним управляться.

Как видно из рассмотренных выше примеров, путь непосредственного вычисления интеграла при применении интегрального признака сходимости не всегда приемлем. Правда, иногда можно прийти к цели путем каких-нибудь косвенных оценок величины этого интеграла, но это уже будет представлять собой самостоятельную задачу, иногда даже более трудную, чем анализ самого ряда.

Следовательно, при изучении рядов ограничиться одним только интегральным признаком сходимости нельзя, и необходимо использовать еще и другие признаки сходимости, быть может, не столь чув-

ствительные, как интегральный признак, но зато более удобные в обращении, более практичные.

Наконец, для того чтобы применение признака сходимости было не только принципиально возможным и практически выполнимым, но и действительно приводило к цели, признак должен быть достаточно

чувствительным.

Такими признаками очевидно являются признаки сходимости

Даламбера

Коши. Они весьма практичны и достаточно широки, но

зато малочувств тельны. Впрочем, как видно из рассмотренных выше

примеров,

х чувств

тельности будет хватать для ответа на весьма

большое ч сло теорет ческих вопросов и решения многих практиче-

задач.

Задачи для решения в аудитории

ских

с помощью при-

Задача 3.

Исследовать на сходимость ряд

знака Даламбера, если:

n 1

а)

;

) un

n n!

n ;

в)

3n 1

;

г)

д)

n2 1

;

(2бАn 1)! 2n 3 3

Задача 4. Исследовать на сходимость ряд an

с помощью ради-

n 1

кального признака Коши:

а)

б)

n 2 n2

в)

3n 5

n ;

;

(4n 3)

n 1

5n 4

г)

arctg

д)

nИ

;

3n2 2n

n 3

с помощью инте-

Задача 5. Исследовать на сходимость ряд an

грального признака Коши, если:

n 1

а)

;

б)

;

в)

3n2

;

1 n2

en3

г)

8 ln2 n

сходится

Ответы

3. а) Ряд расход тся,

) ряд расходится, в) ряд расходится, г) ряд схо-

) ряд сход тся. 4. а) Ряд сходится,

б) ряд расходится, в) ряд

бА5 1 e

, г) ряд сход

тся, д) ряд сходится.

5. а) Ряд расход тся,

) ряд сходится, в) ряд сходится, г) ряд расхо-

Индивидуальные задания

Исследовать сходимость следующих числовых рядов.

4.01а)

n 5

;

)

n 1 2n

;

в)

2 3n

n 1

n 1 n 1 ln n 1

Дn

3n 1

4.02а)

;

б)

3 5n

;

в)

n 1

3n 1

ln7 n

4.03а)

;

б) 2n

4n 5

;

в)

n 1n!

n 1

n 1 n

n2 1

5n 3

4.04а)

;

б)

;

в)

n 1

n 15n 1

5n 1 2n

4.05а)

;

б)

;

в)

n 13n

n 1 7n

Иn 1 n 1 ln n 1

4.06а)

2n 3

;

б)

;

в)

n 1 3n

n 1lnn n 1

n 1

2n 3

4.07а)

;

б)

n 1

;

в)

2n 1

n 12n

n 1

n 1n n

4.08а)

2n 1

;

б)

;

в)

ln4 5n 2

n 1

n 1 6n 1 n

n 1

5n 2

n 1 n

4.09а)

; б)

;

в)

n 1

n 13n

n 1 en

n 1 n

arctgn

4.10а)

;

б)

;

в)

n 1n n 1

n 1nn

n 1 1 n2

4.11а)

;

б)

;

в)

n 1arctgn n2 1

n 13n

n 15n

4.12а)

;

)

;

в)

n 1

бА

4.13а)

2nn

1 ;

)

4n2

в)

n 3n2 .

;

n 1 3 1

n 1 n 1

n 1

4n 1

100n2 n

3n2 1

4.14а)

;

)

;

в)

n 1

n 1 n

100

n 1 n

4n 1 n

3n3 2

4.15а)

;

)

;

в)

n 1n2

n 1

4.16а)

;

б)

lnn n 1 ;

в)

n 1 n 2

n 1

2n 1 n2

n 1

4.17а)

;

б)

;

в)

n 1

n! n

4.18а)

;

б)

Д; в) .

n 1n

n 1 2n

n 1n2

4.19а)

7n 1

;

б)

n 1 n

;

в)

ln n 1 1

n 1

n 12n 1

n 1

n 3

5n 1

Иn

4.20а)

;

б)

;

в)

n 1

3n2 1

2n ;

4.21а)

;

б)

в)

n 15

n 13 n2 1

n 1

<<< < Предыдущая 1 2 3 4 56 / 186 7 8 9 10 11 12 13 14 15 16 17 18 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
07.01.20212.61 Mб42012.pdf
#
07.01.20212.61 Mб42013.pdf
#
07.01.20212.61 Mб1202014.pdf
#
07.01.20212.61 Mб62015.pdf
#
07.01.20212.61 Mб62016.pdf
#
07.01.20212.61 Mб332017.pdf
#
07.01.20212.61 Mб352018.pdf
#
07.01.20212.62 Mб282019.pdf
#
07.01.2021346.19 Кб5202.pdf
#
07.01.20212.62 Mб692020.pdf
#
07.01.20212.62 Mб162021.pdf