Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Сибирская государственная автомобильно-дорожная академия

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

2017.pdf

Скачиваний:

Добавлен:

07.01.2021

Размер:

2.61 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 1617 / 1817 18 > Следующая >>>

Рассмотрим различные решения этого уравнения на примерах задач о вынужденных колебаниях струны с различными граничными и начальными условиями.

5.1. Задача о вынужденных колебаниях струны при отсутствии начальных возмущений

К этой задаче сводится решение неоднородного волнового уравнения (4.39) с однородными граничными и начальными условиями


и		,u(l,t) 0		,	(4.40)
С	u(0,t) 0
	(х, 0) = 0,	и х,0	0.		(4.41)

		t

Её решен былоестро тсяметодом разложения по собственнымфункциям.

В соответств с этим методом на первом этапе решается методом разделен я переменных краевая задача для однородного волно-

вого уравнен я		(4.1) при однородных граничных условиях
(4.4) – (4.5).		А

Как	показано ранее (см. § 3), собственные функции этой
задачи определяются согласно (4.16): Хn х sin					nx		.

						l
На втором		этапе возвращаемся к неоднородному уравнению
			Д
(4.39), и его решение ищем в виде разложения в ряд по собственным
функциям однородной задачи				Un t sin nx '.
	u x,t Un t Хn х

		n 1		n 1		l

При этом удовлетворяются граничные условия (4.40), а задача сводится к отысканию неизвестной функции Un t . Подставляя (4.42) в уравнение (4.39), получим

d2U

n a

f x,t .

sin

(4.43)

l И

n 1

Далее раскладываем в ряд Фурье на отрезке [0, l] по собственным функциям однородной задачи правую часть уравнения (4.43):

F	t sin nx f x,t .		(4.44)

n
n		l
n 1		l

165

При этом

Fn	t	2	l	f x,t sin	nx	dx.	(4.45)

		l
			0		l

Подставляя (4.44) в уравнение (4.43), получим

d2U

n a

sin

F t sin

n 1

Пр равн вая в этом равенстве выражения при одинаковых соб-

ходим

dU 0

ственных функц ях, пр

к уравнению

Сd2U

n a

F t .

(4.46)

dt2

образом

Подставляя далее (4.42) в начальные условия (4.41), находим

Un 0

(4.47)

Таким

отыскание функции

Un t

сводится к решению

задачи Коши для о ыкновенного линейного неоднородного диффе-

ренциального уравнения второго порядка (4.46) с начальными усло-

виями (4.47). Общее решение уравнения (4.46) складывается из обще-

го решения однородного уравнения и частного решения неоднород-

ного уравнения U * t :

(t) C

t cos

ant

t sin

ant

U* t .

(4.48)

В общем случае, при произвольной непрерывной правой части в

уравнении (4.46) частное решение ищется в соответствии с методом

вариации произвольных постоянных в виде

U*n(t) C

t cos

ant

t sin

ant

(4.49)

166

Определитель Вронского, составленный из частных линейно независимых решений однородного уравнения (4.46), равен

cos

ant

sin

ant

sin

ant

cos

ant

Поэтому про зводные

от

варьируемых функций Cn t иDn t

определяются по формулам

иn

Сsin

ant

Cn' t

sin

Fn t ,

бАan 0 l

cos

ant

cos

F t .

(4.50)

Интегр руя д фференциальные уравнения первого порядка

(4.50), находим

Cn t

sin

Fn t d ,

Дn

D t

cos

F t d .

Следовательно, частное решение неоднородного уравнения

(4.46) может быть представлено в виде

ant

U*n(t)

F cos

an t l

F sin

sin

d cos

Fn sin

t d ,

а общее решение согласно (4.48) будет

Un t Cn cos

an t

sin

t d .

Dn sin

(4.51)

167

Из начальных условий (4.47) следует
Cn=Dn= 0.	(4.52)

Подставляя (4.51) с учетом (4.52) в (4.42), найдем закон вынужденных колебаний струны конечной длины при отсутствии начальных возмущениях в виде

l 1

n x

u x,t

Fn sin

t d

sin

(4.53)

a n 1n 0

Уч тывая выражение (4.45) и меняя в (4.53) порядок суммиро-

нтегр рования, можно представить решение задачи

С(4.39) – (4.41) в в де

l 1 t 2 l

n x

u x,t

f , sin

sin

t d sin

a n 1 n

0 l

t l

n x

вания

, sin

sin

d sin

t d

0 0 n 1n

или окончательно

t l

f , d d

(4.54)

u x,t G x, ,t

где введено обозначение

бА2 1 n x an

G x, ,t

f ,

sin

t .

(4.55)

a n 1n

Функция

G x, ,t называется

функцией

источника

или

функцией влияния мгновенного сосредоточенного импульса, прило-

женного на ограниченном отрезке

, 0

. Можно показать, что

в пределе при 0, 0 получим функцию

u x,t G x, ,t

характеризующую влияние мгновенного сосредоточенного импульса

мощности

f , d d .

168

Зная воздействие мгновенной сосредоточенной силы, можно по формуле (4.54) найти закон колебаний струны под действием произвольной непрерывно распределенной силы f(x,t).

Если функция Fn(t) в уравнении (4.46) имеет достаточно простой
вид, то для определения частного решения можно воспользоваться
С
методом подбора частного решения.
5.2. Решен е задачи о вынужденных колебаниях струны
с учетом начальных возмущений
найти		t
Пусть требуется	решение уравнения (4.39) при однород-
ных гран чных услов ях (4.40) и неоднородных начальных условиях
бА
		u(x,0)	x ,
	u(x,0)		f x .	(4.56)

В силу линейности уравнения (4.39) для решения поставленной задачи применим приём редукции, а именно решение исходной на-

чально-краевой задачи может ыть представлено в виде
	u(x,t) x,t w x,t ,							(4.57)
			Д
где функция x,t является решением начально-краевой задачи для
однородного уравнения
			2	a2 2				(4.58)
			t2	a2 2				(4.58)
			t2		t	2	И
с однородными граничными условиями							И
с однородными граничными условиями
	(0,t) l,t 0							(4.59)
и с начальными условиями
		(x,0)			x ,
					x ,
			t
		(x,0) f x .						(4.60)

169

Функция w x,t является решением начально-краевой задачи для неоднородного волнового уравнения

2w	a2	2w	f x,t	(4.61)
t2		t2

С
при однородных граничных условиях
	w(0,t) w l,t 0										(4.62)
и с нулевыми начальными условиями
и
	w(x,0) 0,
			w(x,0)			0.					(4.63)
				t
Задача (4.58) – (4.60) описывает свободные колебания струны,
её решен е звестно [см. § 3, выражения (4.19), (4.22), (4.23]:
		na t					an t		n x
x,t A	cos				B sin			sin		.	(4.64)
x,t A	cos		l		B sin		l	sin	l	.	(4.64)
n 1 n			l			n	l		l

Задача (4.61 ) – (4.63) описывает вынужденные колебания струны при отсутствии начальных возмущений. Её решение представляется в виде разложения в ряды по собственным функциям однородной задачи:

n x

бw x,Аt W t sin

n 1

(4.65)

f x,t F

t sin n x .

n 1

Как было показано, отысканиеДфункции Wn(t) сводится к реше-

нию задачи Коши для обыкновенного линейного неоднородного

дифференциального уравнения второго порядка

d2W

n a

F t

(4.66)

dt2

с однородными начальными условиями

W 0

dWn 0

0 .

(4.67)

170

Суммируя решения задач (4.58) – (4.60) и (4.61) – (4.63), получа-

ем общее решение исходной задачи.

Пример. Найти закон колебаний однородной струны длиной l под действием внешней гармонической силы

F x,t 2 xsin t,

рассчитанной на ед н цу длины струны. Концы струны закреплены. Начальные услов я

u(x,0) U0 x 0,

Сu(x,0)

V0 x

(4.68)

бА

Решен е. Задача приводится к решению уравнения

иu

F x,t

(4.69)

при однородных граничных условиях (4.40) и начальных условиях (4.68). Величины , и – константы.

Так как начальные условия неоднородны, применяем прием редукции, полагая

u(x,t) x,t w x,t .

Функция

x,t определяется

выражением

(4.64). Из

формул

(4.22), (4.23) находим

2g l

n x

4gl

An 0, Bn

x 1

sin

a nl 0

Поэтому

x,t 4gl

sin n at sin n x .

(4.71)

1 1

a n 1

Функция Fn(t) определяется из выражения (4.45):

n x

2 x

n x

Fn t

F x,t sin

sin t sin

171

n x

n 1

sin t xsin

4 1

sin t.

(4.72)

Для определения функции w x,t , используя (4.65) и (4.72), при-

ходим к уравнению

d2W

n a

4 1 n 1

sin t.

dt2

Общее решен е уравнения (4.73) имеет вид

W x,t C

cos

na t

sin

an t

4 1 n 1

sin t . (4.74)

Сl

n a

бАn

Наход м далее произвольные постоянные из начальных условий

(4.68):и

4 l 1 n

(4.75)

Cn 0, Dn

2 n a 2

a n

Следовательно,

W t

4 1 n

n at

sin

sin t

(4.76)

n a 2

2 n a

Подставляя (4.76) в (4.65), находим решение задачи (4.66), (4.67)

в виде

4 1 n

w x,t

n at

n x

. (4.77)

sin

sin t sin

n a

n 1

n a

172

Суммируя решения (4.71) и (4.77), окончательно имеем

w x,t

4 gl

1 1 n

n at

sin

n 1 a 3

1 n

n at

n x

sin

sin t sin

(4.78)

n a

следствием

Из полученного решения следует, что в случае, когда частота

Свнешней возмущающей силы совпадает с одной из собственных час-

тот колебан й струны n

n a

(явление резонанса), отклонения

бА

струны от положен я равновесия неограниченно возрастают. Это, ко-

нечно, является

принятой идеализированной математиче-

ской модели коле ан й, не учитывающей демпфирования.

5.3. Редукция о щей неоднородной начально-краевой задачи

для волнового уравнения

Пусть уравнение и все краевые условия (граничные и началь-

ные) неоднородны и имеют вид

u f x,t .

(4.78)

Граничные условия

u(0,t) t , u l,t t ,

(4.79)

а начальные условия

И(4.80)

u(x,0)

V x

u(x,0) U0 x .

173

Принимаем

u(x,t) x,t w x,t ,

(4.81)

где функция w x,t ищется в виде линейной функции:

w x,t kx b,

а коэффициенты k и b определяются из граничных условий (4.79):

w 0,t b t ,

w l,t kl b kl t t .

Отсюда следует

t t

Поэтому

w x,t t t t

(4.82)

для функции x,t получаются

При этом, как легко у едиться,

однородные гран чные условия:

0,t 0, l,t 0.

(4.83)

Подставляя (4.81) с учетом (4.82) в уравнение (4.78), приходим к

неоднородному уравнению относительно функции x,t :

t t

f x,t

(4.84)

бА

Начальные условия для функции v(x,t) запишутся в виде

(x,0) U0 x w x,0 ,

(x,0)

V x

w(x,0).

(4.85)

Таким образом,

задаче

отыскание

функции

x,t сведено к

(4.84), (4.83), (4.85) с однородными граничными условиями, которая далее решается с использованием приема редукции (см. п. 5.2). Найдя функцию x,t и подставляя её в (4.81), получим окончательное решение исходной задачи (4.78 – 4.80).

174

Задачи для решения в аудитории

Задача 1. Струна закреплена на концах в точках x=0 и x=l, имеет

в начальный момент времени форму параболы u(x,0)

x(l x).

Определить смещение точек струны от оси абсцисс, если начальные

скорости всех точек струны равны нулю.

Задача 2. Найти решение волнового уравнения

2и

приdu

(l,t) 0.

Сследующ х гран чных условиях:

(0,t) 0,

бА

С начальными условиями

и(х, 0) = х,

и х,0 2.

Ответы

1. u x,t

cos 2n 1 at sin 2n 1 x ;

n 0

2n 1 3

2. u x,t

2n 1 x

cos

2n 1

2 n 0

Индивидуальные задания

1. Найти отклонение u(x, t) закрепленной на концах x=0 и x=l однородной горизонтальной струны от положения равновесия, если в начальный момент струна имела форму параболы с вершиной в точке

x l и отклонением вершины от положения равновесия h, а началь- 2

ные скорости отсутствовали. Взяв три первых члена ряда Фурье, най-

175

ти приближенно отклонение струны в точке	x	l	,	если t=0,05	с,

а=5000 м/с, l=30 м.	3

2. Найти закон колебания струны длиной l, если концы струны
закреплены, начальное положение задается функцией f(x)=2, началь-
С
ные скорости отсутствуют, взяв три члена ряда Фурье, найти прибли-
женное отклонение середины струны, если	l=10			м; t=0,01	с,
a=5000 м/с.

3. Найти закон колебания струны длиной l, если в начальный момент времени всем точкам струны сообщена скорость, равная x(l-x). Начальное отклонение отсутствует. Концы струны закреплены. Взяв 3 члена з ряда Фурье, найти приближенно отклонение середины струны, l=20 м, t=0,1 с, материал – сталь. Тстали=21,6·1010 Па,

ρстали=7,8·103 кг/м3.

4. Найти закон сво одных колебаний струны длиной l, закреп-

ленной на концах,			известно положение струны в начальный мо-
если
мент sin x		начальные скорости точки описываются функцией
	l
	бА

sin 2 x . Взяв три члена ряда Фурье, найти приближенное отклонение l

середины струны, если l=10 м, t=0,01 с, а=5000 м/с.

5.Однородный стержень длиной 2l сжат силами, приложенными

кего концам так, что он укоротился до длины 2l(1-ε). При t=0 нагрузка снимается. Найти продольные колебания стержня u(x;t).Взяв три

члена получившегося ряда Фурье, найти приближенно кривую распределения смещения сечения с абсциссой x стержня, если l=10 м;Д

t=0,01 с, 0.5 10 5см, материал – сталь (считать, что точка x=0 находится посередине стержня, обратить внимание, что оба конца стержня свободны и начальная скорость равна нулю, а смещение сечения с абсциссой x пропорционально).

Замечание. По закону Гука смещение любого сечения в началь-

ный момент	пропорционально его	абсциссе, т. е. u(x,0) x.
Тстали=21,6·1010	Па, ρстали=7,8·103 кг/м3.	И

6. Круглый цилиндрический стержень, имеющий в нерастянутом состоянии длину l, закреплен на конце x=0, к другому концу приложена растягивающая сила Q=const. В момент t=0 эта сила снимается. Найти продольные колебания стержня, взяв три члена получившегося ряда Фурье, определить приближенно отклонение свободного

176

конца стержня, приняв l=10 м; Q=100 кг, площадь сечения S=10 см2; t=0,01 с; материал – сталь. Тстали=21,6·1010 Па

Замечание. Точки струны получают начальное смещение u(x,0)=Qх/ТS, где Т – модуль упругости, S–площадь поперечного сечения стержня.

7. Найти закон свободных колебаний струны длиной l, закрепленной на концах, если начальное положение струны задается функцией x(l-x), а начальные скорости отсутствуют. Взяв три первых члена


ряда Фурье,	определ ть приближенно отклонение				струны, если
l=10 м, t=0,02	, a=5000 м/с.
8. Найти закон свободного колебания струны длиной 1 м, закре-
С		известно, что ее натяжение			T и линейная
пленной на концах,
плотность таковы, что		a	T	100 м/с. Начальное положение стру-
если

ны задается функц ей f(x)=(1-2x2+x3), начальные скорости точек струны равны нулю.

9. Струна закреплена на концах x=0 и x=3. В начальный момент форма струны меет в д ломаной О В, где О(0;0); А(2;-0,1); В(3;0). Найти форму струны для лю ого момента времени t, если начальные скорости точек струны отсутствуют. Взяв три первых члена ряда Фурье, найти приближенно отклонение струны в точке А, если t=0,05 с,

a=5000 м/с; l=30 м.	Д
10. Найти закон колебания струны, расположенной на отрезке
[0, l]. КонцыбАструны закреплены. Струна отпущена без начальной ско-

рости, ее начальная форма задана функцией u(x 0) A sin n x , l

A=const,n –целое число. Найтиточкинаибольшегоотклоненияструны. 11. Найти закон колебания струны с Изакрепленными концами x=0, x=l, если начальные скорости всех точек струны равны нулю, а в начальный момент времени струне придана форма параболы

u(x,0) 4h x(l x). l2

12. Найти закон колебания струны с закрепленными концами x=0, x=l, если в начальном положении струна находится в покое, а все точки струны получают начальную скорость 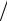4, =const.

177

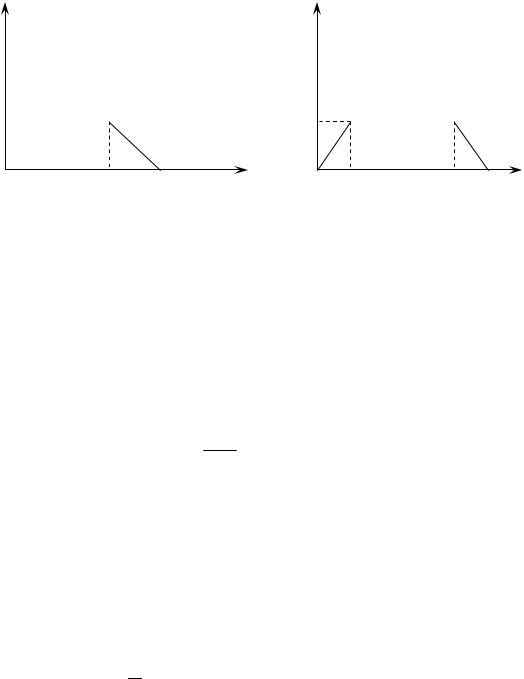
13. Найти закон колебания струны длины l, если ее концы жестко закреплены. Струна отпущена без начальной скорости, а ее начальное отклонение имеет вид (рис. 4.5).

С					u
u
Найти
Найти					a
	h				a
	h
					0 a	π-a π x

0	c		l	x
0	c		l	x
	зображена					Рис. 4.6
	Р с. 4.5					Рис. 4.6
14.	закон коле ания струны, начальная форма смещения
которой		рис. 4.6. Струна отпущена без начальной ско-
рости, ее концы закреплены.
15. Найти закон коле ания струны, которой придана начальная
форма, описываемая функцией
		h		(x l)	l x ;

		Аl

вточке x=-l и x=l. Д

16.Найти закон колебания струны, закрепленной в точках x=0 и x=l. В начальный момент времени струнеИпридана форма кривой u(x,0) = sin3x, струна отпущена без начальной скорости.

17.Пусть струна, расположенная на отрезке [0, l], закреплена на

концах. В начальный момент времени струна находится в покое, все точки струны получают начальную скорость, которая описываетсяu (x,0) sin x

18.Струна закреплена на концах x=0; x=3. В начальный момент

форма струны имеет вид ломаной ОАВ: О(0;0), А(2;-0,1); В(3;0). Найти форму струны для любого момента времени t, если начальные скорости точек струны отсутствуют.

178

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 1617 / 1817 18 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
07.01.20212.61 Mб42012.pdf
#
07.01.20212.61 Mб42013.pdf
#
07.01.20212.61 Mб1202014.pdf
#
07.01.20212.61 Mб62015.pdf
#
07.01.20212.61 Mб62016.pdf
#
07.01.20212.61 Mб332017.pdf
#
07.01.20212.61 Mб352018.pdf
#
07.01.20212.62 Mб282019.pdf
#
07.01.2021346.19 Кб5202.pdf
#
07.01.20212.62 Mб692020.pdf
#
07.01.20212.62 Mб162021.pdf