Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Сибирская государственная автомобильно-дорожная академия

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

2017.pdf

Скачиваний:

Добавлен:

07.01.2021

Размер:

2.61 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 13 14 1516 / 1816 17 18 > Следующая >>>

Решение. Задача сводится к решению однородного волнового уравнения (4.1) при однородных граничных условиях (4.4) – (4.5) и начальных условиях

u х,0 x l x ,

u(x,0)

(4.25)

Для рассматр ваемого случая, очевидно,

Вn 0,

так как соглас-

но (4.3) (х) 0. Подставляя в (4.22)

f х

x l x

после двукратного нтегрирования по частям находим

и2 1 1 n

n 3

(4.26)

Подстановка (4.26) в (4.19) с учетом Вn

0приводит к решению

задачи в виде

cosn at sin

n x

u x,t

(4.27)

n 1

бА

§ 4. Продольные колебания стержня

Стержнем называют тело, размерыДпоперечного сечения которого малы по сравнению с его длиной. Как известноИ, стержень является основным расчётным объектом в сопротивлении материалов.

Будем рассматривать призматический стержень постоянного поперечного сечения с прямолинейной осью. Если стержень предварительно растянут или сжат осевыми силами и в момент времени t = 0 действие сил мгновенно прекращается, то он будет совершать свободные (собственные) продольные колебания.

159

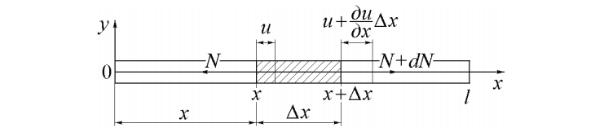
Рис. 4.3

Будем предполагать, что при этом сечения, перпендикулярные к

продольной оси стержня, оставаясь плоскими, будут смещаться толь-

ко вдоль оси абсц сс 0x, совпадающей с продольной осью стержня

что стержень однородный, то есть

( . 4.3). Предполагаем также,

выполнен

з матер ала с постоянной линейной плотностью ρ.

Пусть

u x,t [м] – продольное перемещение поперечного сечения

стержня с

ссой х в момент времени t;

рис

E – модуль упругости материала стержня [Па];

F – площадь поперечного сечения стержня [м2];

l – его длина [м].

Относительноеабсцудлинение (деформация) стержня в сечении с

абсциссой х в момент времени t равно

lim

u x x,t u x,t

u x,t

x 0

Внутренние нормальные силы определяются по закону Гука и

равны:

в сечении х

N F E F EF

u x,t

;

в сечении (x + dx)

u x,t

2u x,t

dN EF

Следовательно, равнодействующая внутренних нормальных сил

упругости, приложенных к элементу стержня, равна

N dN N EF

dx.

160

Эта сила уравновешивается возникающими при продольных колеба-

ниях силами инерции Fdx

Приравнивая в соответствии с принципом Даламбера сумму сил,

действующих на выделенный элемент стержня нулю:

dx Fdx

0 ,

(4.28)

получ м уравнен е продольных колебаний стержня

уравнение

(4.29)

где теперь a

– скорость распространения упругих волн в мате-

бА

риале стержня, скорость звука в материале [м/с].

Как в дно,

малых свободных продольных колебаний

стержня совпадает по форме записи с уравнением малых поперечных

колебан й струны (4.1).

Различие между этими задачами будет проявляться в постановке

граничных условий. Ограничимся случаем консольного защемлённо-

го стержня (рис.4.4).

Рис. 4.4

Очевидно, на левом конце стержня

u 0 0.

(4.30)

Так как на свободном конце стержня внешних сил нет, то равнодействующая внутренних нормальных сил упругости должна быть равна нулю, откуда следует

u l,t	0.	(4.31)

x

161

Как видно, в отличие от задачи о свободных поперечных колебаниях закреплённой по концам струны (4.1 – 4.5), граничные условия теперь являются смешанными, то есть ставятся на функцию и её производную.

Начальными условиями определяются продольные перемещения и скорости поперечных сечений стержня в момент времени t =0:

	u(x,0) f x ,	u(x,0)	х ,	(4.32)

		t
где f x	х – заданные функции.
и
Найдём решен е начально-краевой задачи (4.29 – 4.32) методом
Сразделен я переменных.
Как	ранее, представляя ненулевое частное решение уравнения

(4.29) в в де (4.6), после о ычных преобразований, характерных для
образом
метода разделен я переменных, получим уравнения (4.8) и (4.9).
Подставляя (4.6) в граничные условия (4.30), (4.31), находим
	X(0) Х (l) 0.	(4.33)
Таким	А	теперь прихо-
	, для определения функции X(х)

дим к задаче на со ственные значения (4.11), (4.33). Общее решение уравнения (4.11) имеет вид

X(x) C1 cos x C2 sin x.

Из первого граничного условияД(4.33) получаем

X(0) С2 0,

а из второго граничного условия следует


Х l C1 cos x 0.
Поэтому, чтобы существовало нетривиальное решение задачи,
необходимо принять
	cos x 0,
то есть при l n , n 1,2,... . СледовательноИ, собственные значе-
2
ния равны	2n 1
n	2n 1	n 0,1,2, .	(4.34)
	2l

162

Соответствующие им собственные функции с точностью до постоянного множителя С1 определяются по формуле

Хn	х sin	2n 1 x	.	(4.35)

		2l

Заметим, что собственные функции (4.35) ортогональны на от-

резке [0, l].

При m n меем

2n 1 х

2m 1 х

n m х

m n 1 х

При

sin

cos

n m х

m n 1 х

cos

n m 1

n m

m n

бА

меем

2n 1 х

sin2

1 cos

С учетом (4.34) уравнение (4.8) запишется в виде

a 2n 1

(4.36)

(t)

T (t) 0 .

Его общее решение

T (t) A

cos

a 2n 1 t

sin a 2n 1 t ;

n 1,2,... .(4.37)

Подставляя (4.35),

(4.37) в (4.6) и суммируя частные решения

линейного однородного уравнения (4.29), находим решение задачи в

виде ряда

a 2n 1 t

2n 1 x

(4.38)

u(x,t)

A cos

sin

n 0 n

Произвольные постоянные An и Bn определяем из начальных

условий (4.32):

u(x,t) f x A

sin 2n 1 x ,

n 0

163

u(x,t)

2n 1

2n 1 x

x Bn

sin

n 0

где An

и Bn можно рассматривать как коэффициенты разложения

функций f x и x в ряды Фурье по системе ортогональных функ-

ций sin[(2n+1)πх/(2l)]. Поэтому, согласно (4.22), находим

2n 1

f (x)sin

xdx

2n 1

f (x)sin

xdx,

2n 1

xdx

sin

Сl

2n 1

2n 1 a

(x)sin

xdx

2 l

2n 1

(x)sin

xdx.

2 2n 1

xdx

l 0

sin

Окончательно получ м

2n 1

xdx.

Вn

0 (x)sin

2n 1 a

Подставляя An

и Bn в ряд (4.38), получаем окончательное реше-

ние задачи о сво одных продольных колебаниях консольного защем-

ленного стержня.

бА

§ 5. Решение неоднородного волнового уравнения методом

разложения по собственным функциям

Неоднородным волновым уравнением называется уравнение вида

2и

f x,t ,

(4.39)

в котором f(x,t) – плотность внешней силы,Ивызывающей вынужденные колебания струны, т. с. предел отношения

lim	F x,x x,t	,

x 0	x

где F – внешняя сила, действующая на участок струны [х, х + х] в момент времени t.

164

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 13 14 1516 / 1816 17 18 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
07.01.20212.61 Mб42012.pdf
#
07.01.20212.61 Mб42013.pdf
#
07.01.20212.61 Mб1202014.pdf
#
07.01.20212.61 Mб62015.pdf
#
07.01.20212.61 Mб62016.pdf
#
07.01.20212.61 Mб332017.pdf
#
07.01.20212.61 Mб352018.pdf
#
07.01.20212.62 Mб282019.pdf
#
07.01.2021346.19 Кб5202.pdf
#
07.01.20212.62 Mб692020.pdf
#
07.01.20212.62 Mб162021.pdf