4. ПОКАЗАТЕЛИ ДОЛГОВЕЧНОСТИ

Перечисленные показатели равны математическим ожиданиям соответствующих случайных величин, ресурса, срока службы, времени восстановления, срока сохраняемости.

Гамма-процентный ресурс и срок службы определяются аналогично гамма-процентной наработке и средней наработке.

Выбирая показатели надежности, необходимо руководствоваться следующими рекомендациями [7]:

- общее число показателей надежности должно быть по возможности минимальным;

- следует избегать сложных комплексных показателей; - выбранные показатели должны иметь простой физический смысл;

- они должны допускать возможность проверочных оценок на этапе проектирования, например имитационного моделирования.

Пример расчета показателей надежности.

Исходные данные: N – общее число наблюдаемых объектов; m(t) – число отказавших объектов до наработки t, ч; n – число обнаруженных и

Наработка i-го объекта за время на людений Hi, тыс. мото-ч

Число отказов i-го объекта за наработку H , n

Время пребыванияСi-го объекта в работоспособномi i состоянии tраб.i , тыс. ч

Время пребывания i-го объекта на ремонте tр.i , ч

Время пребывания i-го объекта на техническом обслуживании tо.i , ч

Время восстановления работоспособности объекта с i-ым отказом tв.i, ч

№ отказа

Время восстановления работоспособности объекта с i-ым отказом tв.i, ч

№ отказа

Время восстановления работоспособности объекта с i-ым отказом tв.i, ч

Вероятность безотказной работы за наработку определяется по формуле

˙

Средняя наработка до отказа Тср определяется по формуле

17

5.ОСНОВНЫЕ ЗАКОНЫ РАСПРЕДЕЛЕНИЯ, ИСПОЛЬЗУЕМЫЕ

ВТЕОРИИ НАДЕЖНОСТИ

Наиболее распространенные законы распределения, используемые при оценке надежности технических систем, представлены в таблице 2.

Таблица 2

Наиболее распространенные законы распределения, используемые при оценке надежности технических систем

Закон Пуассона – распределение чисел случайного события ni за время τ. Закон Пуассона используется тогда, когда необходимо определить вероятность того, что в изделии за заданное время τ произойдет один, два

и т.д. отказов [2, 3, 6, 8, 10, 11, 13, 14, 15].

Условием возникновения экспоненциального закона служат внезапные отказы для нормальных условий эксплуатации. Равенство среднеквадратического отклонения среднему времени работы является характерным признаком экспоненциального распределения [2, 3, 6, 8, 10, 11, 13, 14, 15].

Выход из строя большинства машин вызывается различными процессами старения. Поэтому экспоненциальный закон для описания распределения ресурса их узлов не применим. Справедливыми являются нормальный, логарифмически нормальный или закон Вейбулла. Для невосстанавливаемых изделий характерно использовать в качестве

20

показателя надежности вероятность безотказной работы. В таких случаях назначенный ресурс t и параметры наработки до отказа связаны выражениями [4, 6]

– при нормальном законе распределения

;

– при логарифмически нормальном законе

;

– при законе Вейбулла

,

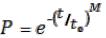где – среднее значение ресурса; – десятичный логарифм среднего

распределения, затем максимум и далее падение, связанное с уменьшением числа работоспособных элементов.

В связи с многообразием причин и условий возникновения отказов в

изменение случайной вел ч ны оказывают влияние многие примерно равнозначные факторы. Наработка до отказа подчиняется нормальному распределению [2, 3, 6, 8, 10, 11, 13, 14, 15].

Время работы резервированных устройств подчиняется гаммараспределению. Если отказ устройства возникает тогда, когда произойдет не менее k отказов его элементов, а сами отказы подчинены экспоненциальному закону распределения с параметром . Среднее время работы устройства до отказа определяется как математическое ожидание [2, 3, 6, 8, 10, 11, 13, 14, 15]

.

При k=1 гамма-распределение совпадает с экспоненциальным. При увеличении k гамма-распределение приближается к симметричному распределению, а интенсивность отказов будет иметь выраженный характер возрастающей функции времени.

21

В случаях, когда поток отказов нестационарный, т.е. плотность потока изменяется с течением времени (как правило, это характерно для систем, выработавших свой ресурс), используется распределение Вейбулла. Оно удовлетворительно описывает наработку деталей по усталостным разрушениям, используется для оценки надежности деталей и узлов автомобилей, подъемно-транспортных и дорожных машин [6, 11]. Интенсивность отказов распределения Вейбулла имеет вид [2, 3, 6, 8, 10, 11, 13, 14, 15]

.

А вероятность отсутствия отказов за время t

.

Возможны следующие варианты [2, 3, 6, 8, 10, 11, 13, 14, 15]:

– при α<1 интенсивность отказов от наработки до отказа убывающие;

– при α=1 распределение преобразуется в экспоненциальное, а интенсивность отказов становится постоянной;

элементом. Число сочетан й определяется выражением [10]

˙

К базовым элементам комбинаторики относятся также перестановки и размещения.

Произвольный упорядоченный набор, составленный из k различных элементов данного n множества, называется размещением из n элементов по k элементов [10]

˙

Произвольная цепочка длины n, составленная из всех элементов данного множества, называется перестановкой этого множества

.

Числа размещений, перестановок и сочетаний связаны равенством

.

22

Еще одним аспектом использования законов распределения вероятностей является генерация случайных величин. Это, как правило, требуется для моделирования объектов, имеющих случайную природу, по известному закону распределения вероятностей.

Процедура генерации случайных величин используется для заполнения диапазона ячеек случайными числами, извлеченными из одного или нескольких распределений.

В MS Excel для генерации случайных величин используются функции из категории Математические:

СЛЧИС () – выводит на экран равномерно распределенные случайные числа больше или равные 0 и меньшие 1(см. рис. 9);

СЛУЧМЕЖДУ (ниж_граница; верх_граница) – выводит на экран случайное число, лежащее между произвольными заданными значениями

23

Рис. 10. Пример использования функции СЛУЧМЕЖДУ

Для получения набора случайных чисел, подчиняющихся закону

распределения все многообразие практических задач сводится к следующим двум вaриантам:

1.Вид функции распределения наблюдаемой случайной величины известен. Задача статистической обработки – получение оценок для показателей надежности с учетом вида функции распределения и характера имеющегося стaтистического материала.

2.Вид функции распределения наблюдаемой случайной величины неизвестен или известен лишь предположительно. В этом случае на основании анализа процессов, приводящих к отказам, опыта эксплуатации аналогичных изделий и предварительного анализа полученной при испытаниях информации (например, по виду гистограммы) принимается некоторая гипотеза о виде функции распределения. Задача обработки –

24

проверить, не противоречат ли экспериментальные данные принятой гипотезе, и оценить параметры этой функции распределения.

Вэтом случае процесс статистической обработки в качестве обязательных должен включать следующие этапы:

– построение вариационного ряда;

– построение гистограммы;

– принятие гипотезы о виде функции распределения;

– оценка точечных значений параметров (для функции распределения предполагаемого типа);

– проверка непротиворечивости экспериментальных данных принятой гипотезе о функции распределения.

Вслучае положительных результатов предыдущего этапа может быть проведена оценка интервальных значений параметров функции

распределения (показателей надежности); в случае отрицательных результатов процедуры проверки гипотезыИпроцесс статистической обработки повторяется, начиная с этапа принятия гипотезы при другом предположении о виде функции распределенияД.АВейбулла (таблица).

чисел с последующим преобразованием его в ряд случайных величин, подчиняющихся одному из законов распределения (см. табл.). Построить график изменения случайных чисел, вариационный ряд и гистограмму распределения.

25

3. Определить вероятность отсутствия внезапных отказов механизма в течение времени t, если интенсивность отказов составляет λ.

4. Определить вероятность безотказной работы подшипника за время t, если его ресурс описывается распределением Вейбулла с параметрами времени ресурса t0 , α .

5. В каких случаях используется распределение Вебулла?

6. Чему равно математическое ожидание случайной величины, подчиняющейся закону распределения Пуассона?

7. Чему равна дисперсия случайной величины, подчиняющейся

26