Суть метода

Код

Задание

Эмпирические моменты

2.1

Найти

оценки

параметров показательного,

равномерного

и

нормального

и

приравниваются к

соответствующим

распределений.

Решение.

теоретическим моментам

Для

показательного

распределения

и распределения. Если

М(Х)

1

x

1

.

распределение имеет:

B

–

один

параметр, то

xB

составляют

уравнение

Для равномерного распределения

a b

M(X)

x

B ;

M(X)

x

;

B

3 B;

2

–

два

параметра, то

a xB

2

составляют

систему

D(X) (b a)

D ;

3 B.

b xB

B

M(X) xB;

12

уравнений

Для нормального распределения

D(X) DB

M(X) a

x

B

;

a

x

B

;

D(X) 2 ИD ; D

B

B

Д

Выравнивание статистического ряда

А

Во всех эмп р ческ х распределениях присутствует элемент

случайности, связанныйбс ограниченностью

выборки. Проводится

Этапы

Задание

построения

1

2

1. Выполнить

Произведено 500 измерений боковой ошибки наводки при

первичную

стрельбе с самолета по наземной цели. Результаты измерений

обработку

(в тысячных долях радиана) сведены в статистический ряд:

опытных

li

(-4;-3]

(-3;-2]

(-2;-1]

(-1; 0]

(0;1]

(1;2]

(2;3]

(3;4]

данных:

ni

6

25

72

133

120

88

46

10

1) построить

статистический

i

0,01

0,05

0,14

0,27

0,24

0,18

0,09

0,02

ряд;

B

И

2) найти

Требуется построить нормальную кривую распределения

основные

измерений боковой ошибки наводки.

числовые

Решение.

Вычислим

приближенно статистическое среднее

характеристи-

Д

ошибки наводки, причем за представителя каждого разряда

ки выборки

примем его середину:

х

В 3,5 0,01 ... 3,5 0,02 0,168;

D

( 3,5)2 0,01 ... 3,52 0,02 0,1682

2,098;

В

1,448

2. Оценить

Выравниваем распределение с помощью нормального закона

параметры

1

2

2

(x a)

и

распределения

f (x)

e

2 .

Закон

зависит

от

параметров

а

и .

и записать тео-

2

А

a

x

;

ретический

С

B

а=0,168;

закон

Согласно

методу

моментов

.

Тогда

б

D .

B

1

(x 0,168)2

1,448, теоретический закон

f (x)

e

21,448

2

1,448

2

3. Найти

Для

нахождения

значений

функции

f (x) воспользуемся

выравниваю-

таблицей функции плотности для нормированной нормальной

щие частоты

1

e

t2

случайной

величины

t

,

значения

которой

2

2

и (t)

табулированы и приведены в прил.

1.

Функции

f (x)

связаны между собой соотношением

f x

1

t . Вычисляем

(ti)

xi xB

значения

f

,

где t

;

x – левая граница i-го

xi

S

i

S

i

разряда.

~

) , где 1–длина i-го разряда. Откуда

Находим рi

f

(xi

Окончание табл. 2.4

1

2

ni npi , ni 500 f (xi).

Например, для первого разряда имеем

t

4 0,168

2,878; (t ) ( 2,878) (2,878) 0,0065;

1

1,448

1

f (t )

0,0065

0,00449;

n 500 0,004 2.

1

1,448

1

Вычисления сведем в таблицу:

-4

-3

-2

-1

0

1

2

3

4

xi

~

0,004

0,025

0,09

0,2

0,27

0,23

0,12

0,04

0,01

f (хi )

ni

2

12

45

100

135

115

60

20

5

4. Построить

И

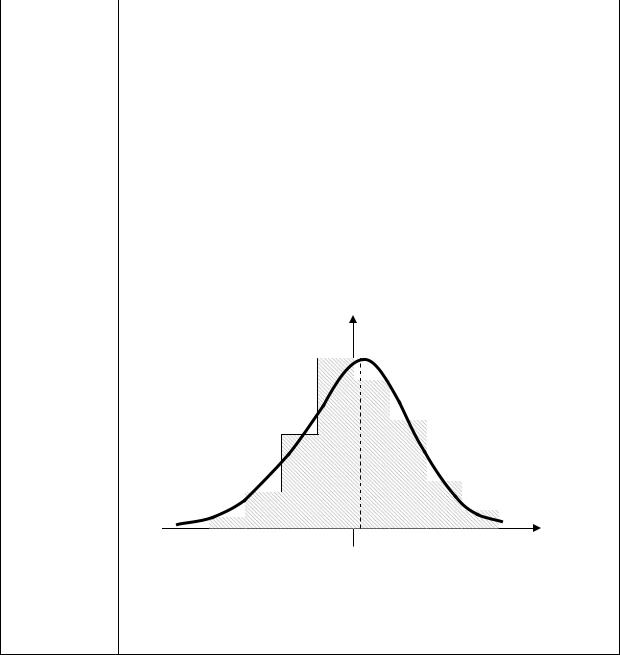
Построим на одном графике гистограмму и выравнивающую

выравниваю-

ее кривую распределения.

щую кривую

Д

распределе-

0,3

f

(x)

ния

А

б

С

-3

-2

-1 0 a 1

2 3

4

-4

Из граф ка в дно, что теоретическая кривая распределения,

сохраняяив

основном

существенные

особенности

статистического распределения, свободна от случайных

неправильностей хода гистограммы, которые, по-видимому,

могут быть отнесены за счет случайных причин

Определение доверительного интервала

Таблица 2.5

Понятия

Код

Задание

, покрывающий

2.2

Интервальная оценка математического

Интервал 1; 2

ожидания нормально распределенного

с

вероятностью

истинное

количественного

признака Х имеет

θ,

значение

параметра

вид

m;24,5 .

Если

выборочная

называется

доверительным,

средняя равна

х

B 22,3,

то значение

вероятность

–

доверительной

вероятностью

(надежностью

m равно…

Решение.

Так

как

интервал

оценки).

симметричен относительно

х

B , то

Доверительный

интервал

часто

выбирается

симметричным

значение точности оценки

относительно

несмещенной

24,5 22,3 2,2,

точечной

оценки

:

искомое значение

P ( ; ) ,

где

m 22,3 2,2 20,1

0 характеризует

точность

И

оценки (чем меньше

, тем

точнее оценка)

Наиболее

часто

встречаются

нормально

распределенные

Д

Интервальные оценки

случайные величины с параметрами

a

и .

для математического ожидания a

приведены в табл. 2.6, для среднего

А

квадратического отклонен я

– в табл. 2.7.

б