
- •Введение
- •КОДИФИКАТОР РАЗДЕЛА «МАТЕМАТИЧЕСКАЯ СТАТИСТИКА»
- •ВВЕДЕНИЕ В МАТЕМАТИЧЕСКУЮ СТАТИСТИКУ
- •Предельные теоремы теории вероятностей
- •Основные законы распределения непрерывных случайных величин
- •Законы распределения случайных величин, связанные с нормальным распределением
- •Глава 1. ВЫБОРКИ И ИХ ХАРАКТЕРИСТИКИ
- •1.1. Справочный материал
- •Задачи математической статистики
- •Основные понятия математической статистики
- •Графическое изображение статистического ряда распределения
- •Эмпирическая функция распределения
- •Числовые характеристики статистического ряда
- •Моменты случайных величин
- •1.2. Задания в тестовой форме
- •Элемент 1.1. Статистическое распределение выборки
- •Элемент 1.2. Основные числовые характеристики выборки
- •Элемент 1.3. Дополнительные числовые характеристики выборки
- •1.3. Варианты заданий для расчетной работы «Первичная обработка статистических данных»
- •1.4. Образец для выполнения расчетной работы «Первичная обработка статистических данных»
- •Глава 2. ЭЛЕМЕНТЫ ТЕОРИИ ОЦЕНОК
- •2.1. Справочный материал
- •Понятие статистической оценки и ее свойства
- •Точечные оценки и их нахождение
- •Выравнивание статистического ряда
- •Интервальные оценки
- •2.2. Задания в тестовой форме
- •Элемент 2.1. Точечные оценки
- •Элемент 2.2. Интервальные оценки
- •2.4. Образец для выполнения расчетной работы «Выравнивание статистических рядов»
- •Глава 3. ПРОВЕРКА СТАТИСТИЧЕСКИХ ГИПОТЕЗ
- •3.1. Справочный материал
- •Понятие статистической гипотезы и ее виды
- •Критическая область и ее нахождение
- •Проверка параметрических гипотез
- •3.2. Задания в тестовой форме
- •Элемент 3.1. Статистические гипотезы
- •Элемент 3.2. Ошибки проверки статистических гипотез
- •Элемент 3.3. Критическая область
- •Элемент 3.4. Проверка статистических гипотез
- •3.3. Варианты заданий для расчетной работы «Проверка гипотезы о равенстве генеральных дисперсий»
- •3.5. Варианты заданий для расчетной работы «Проверка гипотезы о законе распределения генеральной совокупности по критерию Пирсона»
- •4.1. Справочный материал
- •Зависимости между случайными величинами
- •Корреляционное поле
- •Линейная парная регрессия
- •Нелинейная парная регрессия
- •Коэффициент корреляции и его свойства
- •Проверка значимости коэффициента корреляции
- •Корреляционная таблица
- •Корреляционное отношение и его свойства
- •4.2. Задания в тестовой форме
- •Элемент 4.2. Уравнение регрессии
- •Элемент 4.3. Коэффициент корреляции
- •Элемент 4.4. Корреляционное отношение
- •4.3. Варианты заданий для расчетной работы «Подбор уравнения регрессии для бесповторной выборки»
- •4.4. Образец для выполнения расчетной работы «Подбор уравнения регрессии для бесповторной выборки»
- •Библиографический список
1.4. Образец для выполнения расчетной работы «Первичная обработка статистических данных»
Имеются результаты тестирования группы абитуриентов: 5, 3, 3, 3, 3, 4, 5, 5, 4, 2.
Требуется провести первичную обработку статистических данных.
Решение.
1)Построим вариационный ряд: 2, 3, 3, 3, 3, 4, 4, 5, 5, 5.
2)Составим статистический ряд:
xi |
2 |
|
|
3 |
|
|
4 |
5 |
ni |
1 |
|
|
4 |
|
|
2 |
3 |
i |
|
|
|
|
|
|
И |
|
0,1 |
|
|
0,4 |
|
|
0,2 |
0,3 |
|
|
4 |
4 |
|
Д |
|
|||
Контроль: ni 10 |
; i |
1. |
|
|||||
|
|
|
|
|||||
|
i 1 |
i 1 |
|
|
|
|
|
|
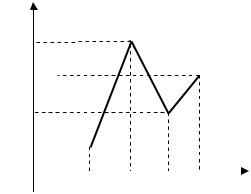
3) Построим полигон частот (рис. 1.1). |
|
|
||||||
|
ni |
|
|
А |
|
|
||
|
4 |
б |
|
|
|
|
||
|
3 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
С |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
0 |
|
|
3 4 5 |
xi |
|
||
|
и2 |
|
||||||
Рис. 1.1. Полигон частот
4) Найдем эмпирическую функцию распределения и построим ее график (рис. 1.2).
|
|
|
|
|
0, |
x 2; |
|
|
|
|
|
|
|
|
|
|
2 x 3; |
|
|
|
|
|
n |
|
0,1, |
|
|
||
F |
|
(x) X x |
x |
|
|
|
|
3 x 4; |
|
|
|
0,1 0,4 0,5, |
|
||||||
|
n |
|
|||||||
|
|
|
|
0,5 0,2 0,7, |
4 x 7; |
||||
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
x 5. |
||
|
|
|
|
|
0,7 0,3 1, |
||||
|
|
|
|
|
|
|
|
|
|
40

F*(x)
1 
0,7 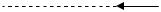
0,5 
|
|
|
|
|
|
|
|
|
|
|
|
0,1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
3 4 |
|
5 |
|
|
x |
|
|
|
|
|
|
||||
|
|
|
|
|
Рис. 1.2. Эмпирическая функция распределения |
|
|
|
|
|||||||||||||||||||||||||||||||
5) Вычислим числовые характеристики выборки: |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
–выборочная средняя: |
х |
В |
|
2 1 3 4 4 2 5 3 |
3,7– |
средний |
||||||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||||
балл по тестированию; |
|
|
|
|
|
|
|
|
|
|
|
10 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
–выборочная дисперсия: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
)2 |
|
|
1 |
4 1 9 4 16 И2 25 3 3,72 |
|
|
|
||||||||||||||||||||||
|
|
D |
|
x2 |
|
( |
|
|
|
|
|
1,01; |
||||||||||||||||||||||||||||
|
x |
B |
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
B |
|
B |
|
|
|
|
|
|
|
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ДS |
|
|
|
1,01 1,12; |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
– исправленная вы орочная дисперсия: |
|
|
9 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
– выборочное среднее квадратическоеА |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
отклонение: B |
|
|
DB |
1; |
||||||||||||||||||||||||||||||||||||
– стандарт: |
S |
|
|
|
S2 |
|
1,06 |
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
– размах выборки: R 5 2 3; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
и3 4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
– мода: |
M0 |
3; |
|
Me |
|
|
|
|
|
|
|
|
3,5; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
– центральный момент третьего порядка: |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
С3 |
|
|
|
|
|
3 |
|
|
|
|
|
3 |
|
|
|
|
|
|
|
3 |
|
|
|
|
|
||||||||||
|
|
|
(2 3,7) 4(3 3,7) |
|
|
2(4 3,7) |
|
3(5 3,7) |
|
0,0237; |
||||||||||||||||||||||||||||||
|
3 |
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
10 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
–асимметрия А 0,02373 0,02; 1,12
–центральный момент четвертого порядка:
4 (2 3,7)4 4(3 3,7)4 2(4 3,7)4 3(5 3,7)4 2,085; 10
~2,085
–эксцесс: Е 1,124 3 1,35.
41

Глава 2. ЭЛЕМЕНТЫ ТЕОРИИ ОЦЕНОК
2.1. Справочный материал
Понятие статистической оценки и ее свойства
Пусть требуется изучить количественный признак генеральной совокупности. Из теоретических соображений удалось установить, какое именно распределение имеет признак. Возникает задача оценки параметров, которыми определяется это распределение. Например, если известно, что признак Х распределен в генеральной совокупности по нормальному закону, то необходимо оценить МХ и, так как эти два параметра полностью определяют нормальное распределение. Обычно имеются лишь данные выборки, полученные в результате n наблюдений: x1,x2, ,xn , через которые выражают
оцениваемый параметр. Рассматривая x1,x2, ,xn |
как значения |
||||||||
независимых случайных величин X1,X2, ,Xn , |
можно сказать, |
что |
|||||||
найти статистическую оценку |
неизвестногоИ |
|
параметра |
|
|||||
теоретического распределения означает найти функцию от |
|||||||||
б |
~ |
|
|
|
|
|
|
|
|
|
~ |
|
,..., Х |
|
) |
|
|
||
наблюдаемых случайных величин |
|
Д(Х , Х |
2 |
n |
, которая и дает |
||||
|
1 |
|
|
|
|||||
приближенное значение оцениваемого параметра. Различают |
|||||||||
и |
|
|
|
|
|
|
|
|
|
точечные и интервальные оценкиА. Точечные оценки определяются |
|||||||||
одним числом и для вы ора «наилучшего» приближенного значения неизвестной генеральной характеристики они должны удовлетворять
свойствам |
несмещенности, |
эффективности |
и |
состоятельности |
|||||||||||
(табл. 2.1). |
С |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Свойства точечных оценок |
|
|
|
Таблица 2.1 |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Понятия |
|
Код |
|
Задание |
|
|
|
|
|
|
|
|
||
|
1 |
|
2 |
|
|
3 |
|
|
|
|
|
|
|
|
|
Несмещенность: M~ M |
|
2.1 |
Выборочная |
|
дисперсия |
|
является |
||||||||
(математическое ожидание оценки |
|
смещенной |
оценкой |
|
генеральной |
||||||||||
|
дисперсии DГ , |
т.к. M(DB ) |
n 1 |
DГ . |
|||||||||||
равно оцениваемому параметру) |
|
||||||||||||||
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
n |
|||
Эффективность: оценка ~n |
имеет |
|
Показать, |
что |
исправленная |
||||||||||
|
выборочная |
дисперсия |
|
2 |
|
|
n |
||||||||
наименьшую |
возможную |
дис- |
|
|
|
|
|
S |
|
|
|
DB |
|||
|
|
|
|
|
|
n 1 |
|||||||||
персию |
|
|
|
является несмещенной оценкой DГ . |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
42

Окончание табл. 2.1
1 |
|
|
|
2 |
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
Состоятельность: |
|
p |
|
Решение. MS2 M |
|
|
n |
|
D |
|
|
|
||||||
|
|
|
|
|
|
|
||||||||||||
|
n |
|
|
|
|
|
|
|
|
|
|
B |
|
|
||||
|
|
n |
|
|
|
|
|
n 1 |
|
|
|
|
||||||
(стремление по вероятности к |
|
|
n |
M DB |
|
n |
|
|
n 1 |
DГ |
DГ |
|||||||
оцениваемому параметру) |
|
|
|
|||||||||||||||
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
n 1 |
n 1 |
n |
|
|
|
|||||||
Точечные оценки и их нахождение
Выборочные характеристики случайной величины Х (выборочная средняя, выборочная дисперсия и др.) могут быть использованы в качестве точечной оценки приближенного значения неизвестной генеральной характеристики (табл. 2.2). К. Пирсоном был предложен метод моментов для нахождения точечных оценок неизвестных параметров распределений в математической статистике (табл. 2.3).
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Д |
|
|
|
|
Таблица 2.2 |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
Оценки математического ожидания и дисперсии |
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
И |
|
|||||||
|
|
|
|
|
|
|
Понятия |
|
|
|
|
|
Код |
|
|
|
|
|
|
|
|
Задание |
|
||||||||||||
Несмещенная |
|
и |
состоятельная |
2.1 |
В результате измерений некоторой |
||||||||||||||||||||||||||||||
оценка |
|
|
|
|
|
математического |
|
физической величины одним прибором |
|||||||||||||||||||||||||||
ожидания |
|
|
|
– |
|
|
|
выборочная |
|
( ез систематических ошибок) получены |
|||||||||||||||||||||||||
средняя: |
|
|
|
|
1 |
|
k |
|
|
|
|
|
|
следующие результаты (в мм): 27, 29, 31. |
|||||||||||||||||||||
x |
|
|
x n |
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
АТогда несмещенная |
оценка |
матема- |
||||||||||||||||||||||||||
|
|
|
|
|
|
B |
|
|
ni 1 i |
i |
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
тического |
ожидания |
и дисперсии |
||||||||||||
Смещенная |
|
и |
|
состоятельная |
2.1 |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
С |
бравна… |
|
|
|
|
|
|
|
|||||||||||||||
оценка |
дисперсии |
|
– |
выбо- |
|
Решение. |
Объём |
|
выборки |
n 3; |
|||||||||||||||||||||||||
рочная дисперсия: |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
1 |
|
n |
|
|
|
|
|
|
2 n |
|
|
и xB |
|
(27 29 31) 29; |
|
|
|||||||||||||||||
D |
|
|
x |
x |
|
|
|
|
3 |
|
|
||||||||||||||||||||||||
B |
|
n |
i 1 |
i |
|
|
B |
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
(27 29)2 |
(29 29)2 (31 29)2 |
||||||||||||
|
|
|
|
|
DB |
1 |
|||||||||||||||||||||||||||||
Несмещенная |
|
и |
состоятельная |
2.1 |
|||||||||||||||||||||||||||||||
|
3 |
||||||||||||||||||||||||||||||||||
оценка |
дисперсии |
|
и |
|
– |
|
|
|
|
|
|
|
|
|
|
2 |
|
3 |
|
|
|
||||||||||||||
исправленная |
|
|
|
|
|
|
выборочная |
|
2,67, тогда S |
|
2,67 4,005 |
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
2 |
|
||||||||||||||||||||||||||
дисперсия |
|
|
|
S |
2 |
|
|
|
n |
|
DB |
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
n 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
стандарт |
|
S= |
|
|
S2 |
|
|
соответ- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
ственно |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
43
