Элемент 1.2. Основные числовые характеристики выборки

Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Сибирская государственная автомобильно-дорожная академия

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

1834.pdf

Скачиваний:

Добавлен:

07.01.2021

Размер:

1.93 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 56 / 216 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 > Следующая >>>

Варианты ответа:

0, x 2;0,1, 2 x 3;

1) F*(x) 0,2, 3 x 4;

0,5, 4 x 5;

0,2,	x 5.

0, x 2;0,1, 2 x 3;

2) F*(x) 0,3, 3 x 4;

0,8, 4 x 5;

1, x 5.

	0,1,	2 x 3;	0,	x 2;
	0,1,	2 x 3;		x 3;
		3 x 4;	0,1,	x 3;
3)	0,3,	3 x 4;		x 4;
3)	F*(x)	4)	F*(x) 0,3,	x 4;
	0,8,	4 x 5;		x 5;
	1,	x 5.	0,8,	x 5;
	1,	x 5.
			И
			1,	x 5.

			Д
	Элемент 1.2. Основные числовые характеристики выборки
	Задание 11. (Выберите один вариант ответа)
	Выборочная средняя – это…
	Варианты ответа: 1) значение изучаемого признака, выбранное
		б	2) среднее взвешенное значение
из середины вариационного ряда;			2) среднее взвешенное значение

признака выборочной совокупности; 3) среднее арифметическое всех
и	совокупности; 4) среднее
значений признака в вы орочнойА

взвешенное квадратов отклонений значений признака около среднего.

1 k

Задание 12.

(Выбер те од н вариант ответа)

Выборочная средняя находится по формуле…

Варианты

ответа: 1)

B xini ;

B n xini ;

i 1

x n .

ni 1

i i

Задание 13. (Выберите один вариант ответа)

Выборочная дисперсия по средней – это… Варианты ответа: 1) наибольшее значение признака;

2) среднее значение признака по выборке; 3) среднее взвешенное значение квадратов признаков по выборке; 4) среднее взвешенное квадратов отклонений значений признака около среднего.

Задание 14. (Выберите один вариант ответа)

Выборочная дисперсия находится по формуле…

Варианты ответа: 1) D

___

;

2) D

___

;

(

)2 x2

___

3) D

Задание 15. (Выберите один вариант ответа)

Статистический ряд распределения баллов в результате тестирования десяти абитуриентов имеет вид

Тогда средний балл абитуриентов равен…

Варианты ответа: 1) 4; 2) 2; 3) 5; 4) 3.

Задание 16. (Выберите один вариант ответа)

Дана выборка: -2, -1, 1, 3, 4.

Выборочное среднее

B и

выборочная дисперсия DB равны ...

Варианты ответа:1) 1; 6,5; 2) 2; 5; 3) 1; 5,2; 4) 1; 6.

Задание 17. (Выберите один вариант ответа)

найдите B …

По данной выборочной дисперсии

0,09

Варианты ответа:1) 0,03; 2) 0,3; 3) 0,81; 4) 0,0081.

Задание 18. (Выбер те од н вариант ответа)

В результате

змеренбй некоторой физической величины одним

прибором (безСс стематических ошибок) получены следующие результаты (в мм): 12,5; 14,5; 16,5. Тогда стандарт S равен…

Варианты ответа: 1) 2; 2) 4; 3) 14,5; 4) 16.

Задание 19. (Выберите один вариант ответа)

Дана выборка объемом n. Если каждый элемент выборки увеличить в 5 раз, то выборочное среднее xB …

Варианты ответа: 1) увеличится в 25 раз; 2) уменьшится в 5 раз; 3) увеличится в 5 раз; 4) не изменится.

Задание 20. (Выберите один вариант ответа)

Дана выборка объемом n. Если каждый элемент выборки увеличить в 2 раза, то выборочная дисперсия DB …

Варианты ответа:1) увеличится в 2 раза; 2) уменьшится в 2 раза; 3) увеличится в 4 раза; 4) не изменится.

Элемент 1.3. Дополнительные числовые характеристики выборки

Задание 21. (Выберите один вариант ответа)

Мода вариационного ряда 1, 4, 4, 5, 6, 7, 8 равна...

Варианты ответа:1) 5; 2) 4; 3) 1; 4) 9.

Задание 22. (Выберите один вариант ответа)

Дан вариационный ряд 15, 15, 15, 15, 18, 20, 22, 24, 24. Его мода имеет частоту, равную …

Варианты ответа:1) 15; 2) 4; 3) 2; 4) 18.

Задание 23. (Выберите один вариант ответа)

Дано статическое распределение выборки объемом n 18:

	xi	15		17	20	28	29
	ni	6		1	n3	И	5
Тогда	мода выборки равна …				Д
Варианты ответа:1) 15; 2) 29; 3) 4; 4) 20.
Задание 24. (Выберите один вариант ответа)
Дано статистическое распределение выборки

	xi	2	б		4	5	7
	xi	2		3	4	5	7
	ni	2		1	2	3	7
		и		А
Тогда медиана равна …				А

Варианты ответа: 1) 3; 2) 4; 3) 5; 4) 7.

ВариантыСответа: 1) 6; 2) 7; 3) 8; 4) 9.

Задание 25. (Выбер те од н вариант ответа)

Даны вариационные ряды: 2, 2, 2, 3, 4, 5, 5 и 3, 4, 4, 4, 6, 7, 8, 8.

Сумма медиан этих рядов равна …

Задание 26. (Выберите ответы согласно тексту задания)

Статистический ряд распределения имеет вид

		xi	0	1	2	3	4	5
Установите		ni	1	2	1	1	2	3
Установите		соответствие между характеристиками выборки и их
числовыми значениями:
1)	выборочное среднее;					а) 3;
2)	выборочная дисперсия;					b) 5;
3)медиана;						c) 3,2;
4)	мода.					d) 2,5.

Задание 27. (Выберите один вариант ответа)

Для выборки 1, 2, 3, 3, 4, 5 центральный эмпирический момент 3-го порядка равен…

Варианты ответа: 1) 18; 2) 6; 3) 3; 4) 0.

	Задание 28. (Выберите один вариант ответа)
	Статистический ряд распределения имеет вид
	xi	2	5	7	8
	ni	2	5	2	1
	Тогда начальный эмпирический момент 1-го порядка равен …
	Варианты ответа: 1) 5,1; 2) 5; 3) 51.
	Задание 29. (Выберите один вариант ответа)
					И
	Для выборки 1, 2, 3, 3, 4, 5 коэффициент асимметрии равен…
	Варианты ответа: 1) -1; 2) 1; 3) 0.
			Д
	Задание 30. (Выберите один вариант ответа)
	Для выборки 1, 2, 3, 3, 4, 5 коэффициент эксцесса …
	Варианты ответа: 1) меньше нуля;				2) больше нуля; 3) равен
нулю.			А
нулю.
	Элемент 1.4. Геометрическое изображение
	статистического ряда
	и
	Задание 31. (Выбер те ответы согласно тексту задания)
	С
	Установите соответствбе между геометрическим изображением
статистического ряда		его названием:
1.	2.				3.
	а) график статистической функции распределения; б) полигон
частот; в) гистограмма частот.

Варианты ответа: 1) 1-а; 2-б; 3-в; 2) 1-б; 2-в; 3-а; 3) 1-в; 2-а; 3-б.

Задание 32. (Выберите один вариант ответа)

Площадь гистограммы частот равна...

Варианты ответа: 1) 1; 2) 100; 3) объему выборки.

Задание 33. (Выберите один вариант ответа)

Площадь гистограммы относительных частот равна...

Варианты ответа: 1) объему выборки; 2) 1; 3) 100.

Задание 34. (Выберите один вариант ответа)

Эмпирическая функция распределения определяет…

Варианты ответа: 1) частость события Х x ; 2) частость события Х x ; 3) вероятность события Х x ; 4) вероятность события Х x .

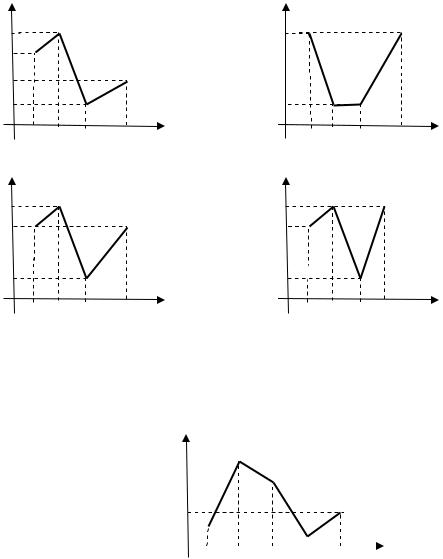
Задание 35. (Выберите несколько вариантов ответа)

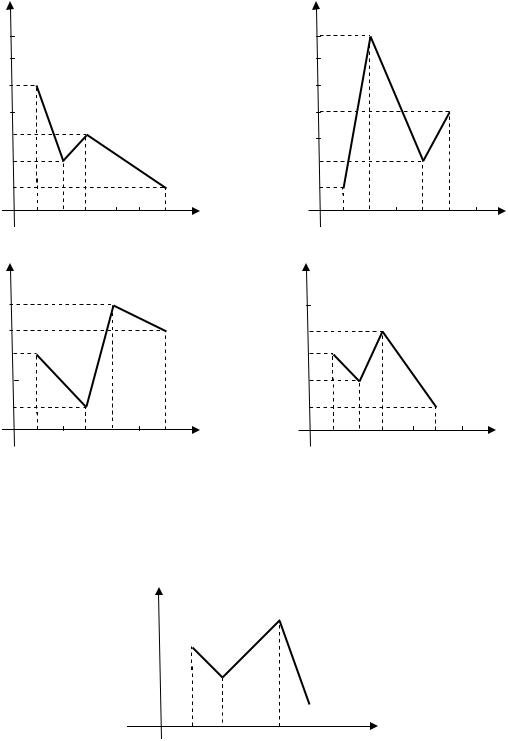
Выборками, заданными полигонами частот, объем которых равен

10, являются…
Варианты ответа:											И
ni									ni		И
ni									ni
4									4	Д
3									3	Д
3									3
2									2
1								А
1									1
0	1	2	3	5		xi	б		0		1 2	3	5 xi
2							б		2
1)								2)
ni				и					ni
4				и					4
4									4
3			С						3
1			С						1
1									1
0	1	2	3	5		x			0	1 2		3 4	x
3)						i		4)					i
3)								4)
Задание 36. (Выберите один вариант ответа)
Из		генеральной			совокупности					извлечена			выборка объемом
n 67, полигон частот которой имеет вид

0 1 3 5 7 9 xi

Тогда число вариант xi 9 в выборке равно …

Варианты ответа:1) 10; 2) 12; 3) 11; 4) 14.

Задание 37. (Выберите несколько вариантов ответа)

Укажите полигоны частот, соответствующие статистическим распределениям, максимальная частота вариант которых равна 5.

Варианты ответа:

ni					ni
7					7
6					6
5					5
4					4
3					3
2					2	И
1					1	И
1					1
0	1 2 3 4 5 6		xi		Д
0	1 2 3 4 5 6		xi		0	1 2 3 4 5 6
1)					2)
n					ni
i				А
i
5			б		5
4			б		4
4					4
3		и			3
2		и			2
2					2
1	С				1
0	С		xi		0	1 2 3 4 5 6
0	1 2 3	4 5 6	xi		0	1 2 3 4 5 6
3)				4)

Задание 38. (Выберите один вариант ответа)

Выборочная средняя выборки, полигон относительных которой задан на рисунке, равна...

частот

0,4

0,3

0,2

0,1

Варианты ответа:1) 3; 2) 2,8; 3) 4; 4) 2,5.

Задание 39. (Выберите один вариант ответа)
Выборочная дисперсия равна 1,2. Она соответствует выборке,
представленной полигоном относительных частот …
Варианты ответа:
i								i
0,5								0,5
0,4								0,4
0,3								0,3
0,2								0,2
0,1								0,1
0	1	2 3 4	5		x				0	1	2 3 4	5	x
1)						i		2)					i
1)								2)
i									i	И
0,5									0,5
0,4									0,4
0,3									0,3
0,2									0,2
0,1									0,1

0	1	2 3 4	5		x				0	1	2 3 4	5	x
3)					i			4)					i
								Д
Задание 40. (Выберите один вариант ответа)
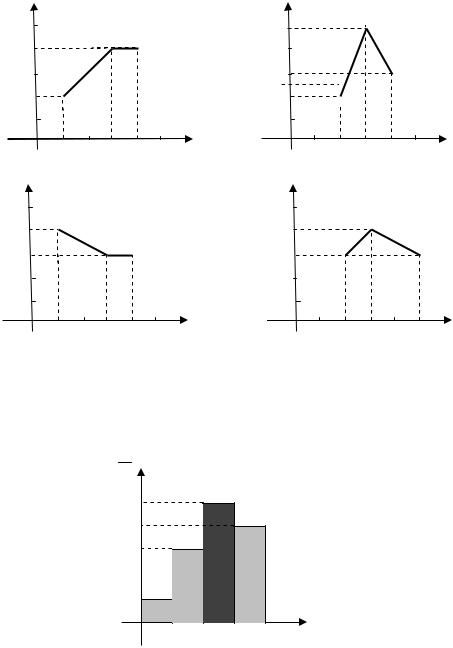
По выборке		объемом		n 100				построена			гистограмма			частот.
Тогда значение а		равно…				А
		ni	б
		h
		и
		18
		a
		12
	С
		4
		0		2		4	6	8		xi
Варианты ответа: 1) 17; 2) 16; 3) 66; 4) 15.

Ответы к заданиям в тестовой форме: 1. 2). 2. 1). 3. 3). 4. 1), 2). 5. 2). 6. 3).

7. 2). 8. 3). 9. 4). 10. 2). 11. 2). 12. 3). 13. 4). 14. 1). 15. 4). 16. 3). 17. 2). 18. 2). 19. 3). 20. 3). 21. 2). 22. 2). 23. 1). 24. 2). 25. 3). 26. 1) - а); 2) - с); 3) - d); 4) - b). 27. 4). 28. 1). 29. 3). 30. 1). 31. 2). 32. 3). 33. 2). 34. 2). 35. 1), 2). 36. 3). 37. 1), 3).

38. 2). 39. 1). 40. 2).

<<< < Предыдущая 1 2 3 4 56 / 216 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
07.01.2021333.26 Кб3183.pdf
#
07.01.20211.92 Mб11830.pdf
#
07.01.20211.93 Mб21831.pdf
#
07.01.20211.93 Mб221832.pdf
#
07.01.20211.93 Mб51833.pdf
#
07.01.20211.93 Mб951834.pdf
#
07.01.20211.94 Mб21835.pdf
#
07.01.20211.94 Mб21836.pdf
#
07.01.20211.94 Mб41837.pdf
#
07.01.20211.95 Mб251838.pdf
#
07.01.20211.95 Mб01839.pdf