1

2

3

Построение дискретного ряда

1.1

частостей: на каждом интервале

52

56

60

xi

вычислим середину x

xi xi 1

i

0,1

0,2

0,15

i

2

64

68,5

xi

i

1

i

0,15

0,4

Д

Таблица 1.4

Полигон и гистограмма частот

И

Понятия

Код

Задание

1

2

3

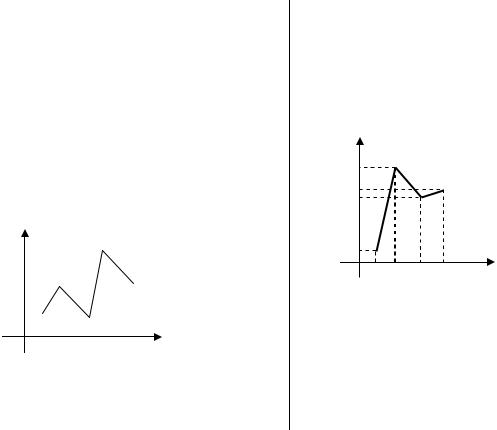
Полигоном частот

б

1.4

Из

генеральной

совокупности

(относительных

частот) называют ломаную, отрезки,

А

извлечена выборка объёмом n 50,

которой соединяют точки

(xi

,ni ),

полигон частот

изображен на

и

12

где

xi

– варианты; ni

–

рисунке.

соответствующие им частоты ( ли

ni

точки

(xi, i),

С

i

–

здесь

20

относительные частоты)

ni ( i )

3

xi

1 2 3 4

xi

Чему равно число вариант x4 4 в

выборке?

Решение. Известно, что

3 20 12 n4 50,

откуда n4 15

1

2

3

Гистограммой частот

1.4 При выборке

объёма

n 60

(относительных частот) называют

построена гистограмма частот.

ступенчатую фигуру, состоящую из

ni

прямоугольников,

у

которых

h

основания

– частичные

интервалы

xi,xi 1

длины

i xi 1 xi ,

а

b

высоты равны отношению

ni

–

12

i

плотность

частоты

(высоты

i

–

4

i

0

2

4 6

xi

плотность относительной частоты).

ni

И

i

Чему равно значение b,

как

выглядит

дискретный

статистический ряд?

Решение.

Площадь

гистограммы

частот равна объему выборки,

xi

следовательно,

2 4 2 12 2 b 60,

Замечание.

Площадь гистограммы

значит, b 14.

Д

по

гистограмме

частот

равна

объему

вы орки,

Составим

статистический ряд. Имеем 2;

площадь гистограммы частостей –А

xi xi 1 ;

ni

2

:

единице.

xi

ni

Гистограмма относительныхибчастот

2

(частостей)

–

это

стат

ст

ческ й

1

3

5

xi

аналог

функции

плотности

f (x)

ni

8

24

28

Таблица 1.5

Эмпирическая функция распределения и её свойства

Понятия

Код

Задание

Эмпирической

1.4

Статистическое

распределение

выборки

(статистической)

имеет вид

функцией

распределения

xi

1

3

9

называется функция F*(x),

ni

5

4

11

определяющая

для

каждого

значения

x

Составить

эмпирическую

функцию

относительную

частоту

распределения.

события X x:

Решение.

Найдем

объём

выборки

F*(x) X x

nx

,

n 5 4 11 20.

x 1:

F*(x) 0

n

Здесь наименьшая варианта

где nx – число вариант;

при x 1.

1

меньших

x

(x R);

n –

При 1 x 3 значение

x1 1 наблюдалось 5

объём выборки.

Д

5

раз, тогда

F*

(x)

0,25.

Свойства эмпирической

20

и x2 3

функции:

При 3 x 9

значения

x1 1

А

5 4 9

раз,

значит,

*

наблюдались

1. 0 F

(x) 1.

9

И

2. F*(x)

–

неубывающая

F*(x)

0,45.

функция.

б

20

Варианта x3 9 наибольшая в выборке, тогда

3. Если x1 и xk –

F*(x) 1

при x 9. Окончательно получаем

наименьшая и наибольшая

варианты

соответственно,

0

при x 1;

*

С

то F (x) 0

*

0,25

при1 x 3;

при

x x1

F

F*(x) 1

при x x

и

(x)

при3 x 9;

k

0,45

1

при x 9.

Строим

график

эмпирической

функции

распределения

F*(x)

1

1

3

9

x

Понятия

Код

Задание

1

2

3

n

средняя

1.2

И

Выборочная

По результатам контрольной работы группа

n

–

для

не-

студентов набрала баллы: 1, 3, 4, 5, 3, 2, 3, 3,

x

B xi

5,

5,

4, 4, 2, 5, 5. Найти основные

i 1

Д

сгруппированной выборки,

характеристики выборки.

1

k

–

для

Решение.

Составляем вариационный ряд: 1,

x

B

x n

2, 2, 3, 3, 3, 3, 4, 4, 4, 5, 5, 5, 5, 5.

i 1

Составим дискретный статистический ряд:

сгруппированной выборки.

б

Характеризует

среднее

15

1

2

3

4

5

x

значение

случайной

i

ni

1

2

4

3

5

величины

и

ОАъём выборки n 15. Находим

x

B

1

(1 1 2 2 3 4 4 3 5 5) 3,6

–

средний балл за контрольную работу в

группе

Выборочная дисперсия

1.2

D

1

((1 3,6)2

1 (2 3,6)2 2

1

k

B 2

B

15

DB

xi

x

ni

4 (4 3,6)2 3

n i 1

С

(3 3,6)2

___

(5 3,6)2

5) 1,57

или D

x2 (

x

B

)2.

B

B

или

Характеризует

разброс

1

значений

случайной

DB

(1 1 2

2

2 3

2

4 4

2

3 5

2

5)

величины вокруг

x

B

15

3,62

1,57

Выборочное

среднее

1.2

квадратическое

B

1,25

1,57

отклонение B DB

Окончание табл. 1.6

1

2

3

Исправленная

выборочная

1.2

15

дисперсия

S

2

n

1,57 1,68

2

14

S

DB

n 1

Исправленное выборочное

1.2

среднее

квадратическое

S

1,68 1,3

отклонение

(cтандарт)

S

S2

Таблица 1.7

Дополнительные числовые характеристики положения

Понятия

Код

И

Задание

Мода

M0*

–

вариант,

1.3

Мода вариационного ряда 1, 4, 4, 5, 6, 8, 9

имеющий

наибольшую

равна...

M0* 4, т.к.

Решение.

этому

варианту

частоту

соответствует наибольшая частота n2 2

Me*

А

Медиана

–

значение

1.3

Даны вариационные ряды: 2, 2, 3, 3, 4, 5, 5

признака,

и 2, 3, 4, 5, 6, 7, 8, 9. Сумма медиан этих

б

приходящееся на

рядовДравна …

середину ряда

Решение. 1-й вариационный ряд состоит из

7 элементов, значит, медианой служит 4-е

С

значение:

Ме

3.

2-й вариационный ряд содержит 8 членов,

и

тогда медиану находят как полусумму

серединных вариантов, т.е. Me*

4 6

5.

Тогда сумма медиан рядов равна 8

2