Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Сибирская государственная автомобильно-дорожная академия

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

1834.pdf

Скачиваний:

Добавлен:

07.01.2021

Размер:

1.93 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 1920 / 2120 21 > Следующая >>>

4.3. Варианты заданий для расчетной работы «Подбор уравнения регрессии для бесповторной выборки»

Получены результаты наблюдений над случайными величинами

Х и Y:

x	1			2				3		4		5
y	y1			y2			y3			y4		y5
Требуется:
1) построить точечный график зависимости X от Y;
2) по	расположению				точек		на		плоскости		выбрать	вид
гипотетической функциональной связи между Х и Y;
3) определить параметры уравнения регрессии, используя												метод
наименьших квадратов (МНК);									И
наименьших квадратов (МНК);
4) записать уравнение				регрессии и					построить		теоретическую
кривую;							Д			Х и Y, используя
5) оценить тесноту связи между величинами										Х и Y, используя
коэффициент корреляции и корреляционное отношение.
						А
					Вариант 1
x	1			2				3		4		5
y	4,3			5,3			3,8			1,8		2,3
		и			Вариант 2
					Вариант 2

x	1			2				3		4		5
y	С		б5,7				4,2			2,2		2,7
y	4,7		б5,7				4,2			2,2		2,7
					Вариант 3
x	1			2				3		4		5
y	4,9			5,9			4,4			2,4		2,9
					Вариант 4

x	1			2				3		4		5
y	5,1			6,1			4,6			2,6		3,1
					Вариант 5

x	1			2				3		4		5
y	3,9			4,9			3,4			1,4		1,9
					Вариант 6

x	1			2				3		4		5
y	5,2			6,2			4,7			2,7		3,2

113

Вариант 7

x	1	2	3	4	5
y	5,5	6,5	5,0	3,0	3,5

Вариант 8

x	1	2	3	4	5
y	5,7	6,7	5,2	3,2	3,7

Вариант 9

x	1	2	3	4	5
y	5,9	6,9	5,4	3,4	3,9

Вариант 10

x	1		2		3	И		5
x	1		2		3		4	5
y	4,6		5,6		4,1		2,1	2,6
			Вариант 11

x	1		2		3		4	5
y	4,8		5,8	А			2,3	2,8
y	4,8		5,8		4,3		2,3	2,8
			Вариант 12
					Д
x	1		2		3		4	5
y	4,4		5,4		3,9		1,9	2,4

		и
			Вариант 13
x	С		б2		3		4	5
x	1		б2		3		4	5
y	4,1		5,1		3,6		1,6	2,1
			Вариант 14

x	1		2		3		4	5
y	2,8		3,8		2,3		0,3	0,8
			Вариант 15

x	1		2		3		4	5
y	3,3		4,1		2,8		0,8	1,5
			Вариант 16

x	1		2		3		4	5
y	3,1		4,3		2,8		1,7	0,6

114

Вариант 17

x	1	2	3	4	5
y	3,3	4,1	2,8	0,8	1,5

Вариант 18

x	1	2	3	4	5
y	3,7	4,5	3,3	1,2	1,5

Вариант 19

x	1	2	3	4	5
y	3,7	2,1	2,4	5,1	0,7

Вариант 20

x		1			2			3					И			5
x		1			2			3						4		5
y		3,3			4,3			2,8						0,8		1,3
					Вариант 21

x	1		2		3	4						5		6	7	8
y	17,2		9,5		7,3	А					5,1			4,6	4,2	4,1
y	17,2		9,5		7,3	5,6					5,1			4,6	4,2	4,1
					Вариант 22
x	1		2		б				Д5					6	7	8
x	1		2		3	4			Д5					6	7	8
y	1,2		5,3		6,9	7,8					8,2			8,5	8,7	8,9
				и
					Вариант 23
x	1		С		3		4					5		6	7	8
x	1		2		3		4					5		6	7	8
y	12,8		6,9		5,2	4,0					3,4			3,1	2,7	2,4
					Вариант 24
x	1		2		3		4					5		6	7	8
y	2,2		-1,6		-2,6	-3,1				-3,5				-4,0	-4,1	-4,2
					Вариант 25

x	1		2		3	4						5		6	7	8
y	13,8		4,3		1,0	-0,2				-1,1				-1,8	-2,2	-2,6

Замечание. В вариантах 1–20 имеет место линейная приближающая функция, в вариантах 21–25 – гиперболическая приближающая функция.

115

4.4. Образец для выполнения расчетной работы «Подбор уравнения регрессии для бесповторной выборки»

Получены результаты наблюдений над случайными величинами

Х и Y:

x	12		16		25			38		43		55			60		80		90		100
y	28		40		38			65		80		101			95		125		183		245
Требуется:
1)	построить точечный график зависимости X от Y;
2)	по расположению точек на плоскости выбрать вид
гипотетической функциональной связи между Х и Y;
3)	определить параметры уравнения регрессии, используя																			метод
наименьших квадратов (МНК);
4)	записать уравнение регрессии и построить теоретическую
кривую;											Д							Y, используя
5)											Д
5)	оценить тесноту связи между величинами Х и
коэффициент корреляции и корреляционное отношение.
Решение.									А					И
1)	Построим эмпирическую линию регрессии Y на Х (рис. 4.2).
		250
		250				и
		200				и
		200
		150

				С				б
		100


		50



		0


		10			20		30	40	50	60	70		80		90	100

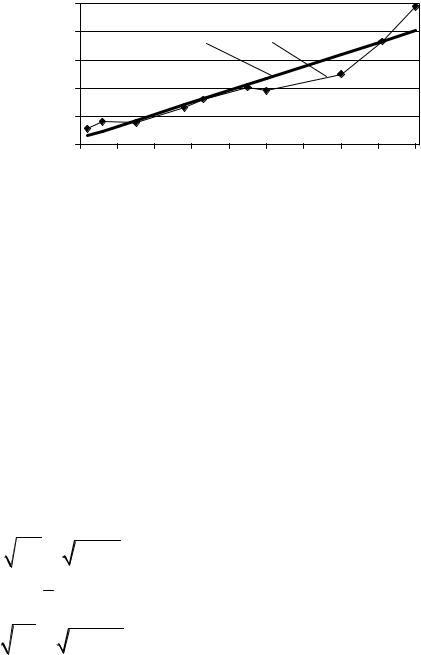
Рис. 4.2. График эмпирической линии регрессии

2)По расположению точек на плоскости выбираем линейную регрессию Y на Х: yх ax b.

3)Определим параметры a и b, используя метод наименьших

квадратов (МНК). Система нормальных уравнений МНК:

116

	n	n	n
a x2		b x x y ;
	i	i	i	i
	i 1	i 1	i 1	Исходные данные и все расчеты
	n		n	Исходные данные и все расчеты
	a x b n y .
	i 1	i	i
	i 1		i 1

необходимых сумм представим в табл. 4.11.

Таблица 4.11

Вспомогательные расчеты для решения задачи

	i		xi		yi			xi2	yi2					xy			f(xi)		(yi				)2			(f (xi )				)2
	i		xi		yi			xi2	yi2					xy			f(xi)		(yi			y	)2			(f (xi )			y	)2
1			12	28			144		784				336			15				5184							7225
2			16	40			256		1600				640			23,5				3600							5852,25
3			25	38			625		1444				950			42,625				3844						3291,891
4			38	65			1444		4225				2470			70,25				1225						885,0625
5			43	80			1849		6400				3440				И			400						365,7656
5			43	80			1849		6400				3440			80,875				400						365,7656
6			55	101			3025		10201				5555			106,375				1						40,64063
7			60	95			3600		9025				5700			117				25							289
8			80	125			6400		15625					Д						625							3540,25
8			80	125			6400		15625			10000				159,5				625							3540,25
9			91	183			8281		33489			16653				182,875				6889						6868,266
10			100	245			10000		60025			24500				202				21025							10404
Итого			520	1000			35624				А					1000				42818
Итого			520	1000			35624		142818			70244				1000				42818					38762,125
									б
		Пользуясь вспомогательными расчетами, составляем систему
нормальных уравнений МНК:
520b 35624a								и							520b 35624a 70244;
520b 35624a						70244;									520b 35624a 70244;

10b 520a 1000.															b 100 520a.
					С										a 2,125;
520(100 520a) 35624a 70244;															a 2,125;

b 100 520a.															b 10,5.				y		x 2,125x 10,5.
		4) Искомая линия регрессии будет иметь вид																	y		x 2,125x 10,5.
Внесем прогнозируемые значения Y в табл. 4.12 и построим график
линии регрессии (рис. 4.3).
								Прогнозируемые значения Y																Таблица 4.12
								Прогнозируемые значения Y
	x		12		16			25	38	43				55			60	80						90				100
	y	x	15		23			43	70	80				106			117	160						180				202

117

250
200			1		2
			1		2
150
100
50
0
10	20	30	40	50	60	70	80	90	100

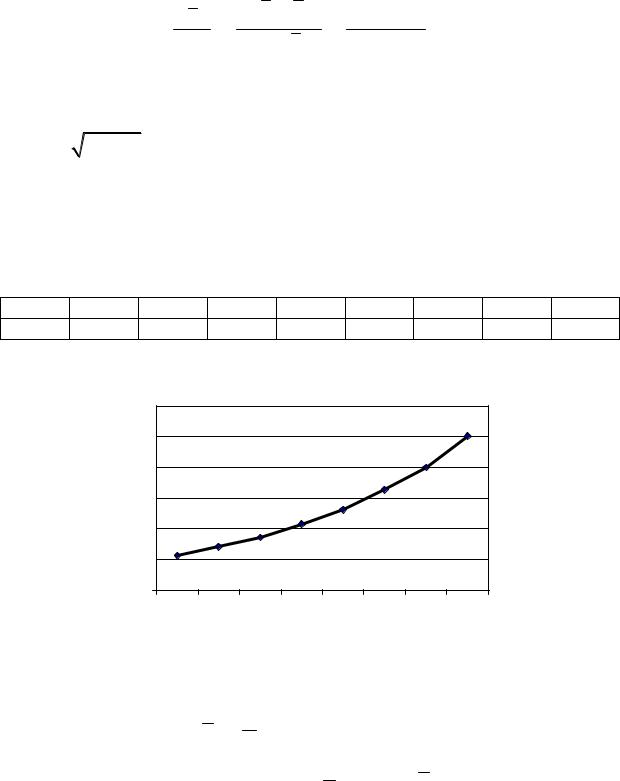
Рис. 4.3. График эмпирической (1) и теоретической (2) линий регрессии

5) Оценим тесноту связи между коррелируемыми величинами Х и

___

xy x y

Y с помощью выборочного коэффициента корреляции r

520

SX SY

Имеем

52 – общее среднее значение по x;

1000

– общее среднееДзначение по y;

100

n10

xi yj

		i			j							70244				7024,4;
xy		i			j							70244
xy
					n							10					б
2			2				2	35624									2			А
2			2				2	35624									2			А
SX	x				x										52			3562,4-2704 858,4;
SX	x				x							10			52			3562,4-2704 858,4;
												10
SX				SX2										29,2;
SX				SX2						858,4				29,2;
											142818и
											142818и
S2	y2					y	2									1002			14281,8-10000 4281,8;
S2	y2					y										1002			14281,8-10000 4281,8;
Y												10
									С
S			S2						С

									4281,8 65,4.
Y					Y								7024,4 52 100									1824,4
	Откуда r												7024,4 52 100									1824,4	0,95 1.
	Откуда r																						0,95 1.
									xy					29,2 65,4							1909,68
														29,2 65,4							1909,68

Следовательно, по шкале Чеддока можно говорить об очень высокой линейной зависимости между коррелируемыми величинами.

Для проверки линейности корреляционной зависимости используем корреляционное отношение и коэффициент детерминации. Найдем теоретический коэффициент детерминации:

118

			2		(yx y)			2		38762,125
	2		yx		(yx y)					38762,125
	теор		2y		(y y)2						42818	0, 9053,
						i
т.е. дисперсия, выражающая влияние вариации фактора Х на
вариацию Y, составляет 90,53 %.
Тогда			корреляционное								отношение				равно
теор	0,9053 0,9515,				следовательно,						можно говорить о большой,
сильной зависимости между коррелируемыми величинами.
Имеем rxy теор ,				что подтверждает существование линейной
зависимости между величинами.
Замечание. Рассмотрим случай нелинейной зависимости между
переменными Х и Y:
х	-4,38	-3,84		-3,23			-2,76			-2,22		-1,67		-1,13	-0,60
y	2,25	2,83		3,44			4,31				5,25	6,55		8,01	10,04
Построим по данным таблицы точечный график (рис. 4.4).
	12										И
	12								Д
	10
	8
	8					А
	6

	4			б
	2			б
	2		и
	0		и
		-4,38 -3,84 -3,23					-2,76		-2,22		-1,67	-1,13	-0,6
	Рис. 4.4. График эмпирической линии регрессии
	С
Из графика видно, что приближающую функцию целесообразно
считать гиперболой: yx				a b. Приведем уравнение к линейному
					x		u 1 .
виду с помощью подстановки							u 1 .			Тогда		y	аu b. Составим
									x			u
вспомогательную табл. 4.13.									x
вспомогательную табл. 4.13.

119

																Таблица 4.13
				Вспомогательные расчеты для решения задачи

i		ui		1				yi					ui yi			u2
i		ui		xi				yi					ui yi			u2
				xi													i
1		-0,23						2,25				-0,52				0,05
2		-0,26						2,83				-0,74				0,07
3		-0,31						3,44				-1,07				0,10
4		-0,36						4,31				-1,55				0,13
5		-0,45						5,29				-2,38				0,20
6		-0,60						6,55				-3,93				0,36
7		-0,88						8,01				-7,05				0,77
8		-1,67						10,04			-16,77					2,79
∑		-4,76						42,72			-34,01					4,47

		Составим нормальную систему МНК:											И
		Составим нормальную систему МНК:
4,47а 4,76b 34,01;								а 5,25;
										Д
4,76а 8b 42,72;								b 2,19.								5,25
									А					y	х 2,19	5,25
		В результате имеем уравнение регрессии												y	х 2,19		.
								б								x
		4.5. Варианты заданий для расчетной работы
							и
«Корреляционно-регрессионный анализ статистических данных
						для сгрупп рованной выборки»
	Получены результаты наблюдений двумерной случайной
величины (X; Y):

							Y	y		y				…		y
			Х		С			y		y				…		y
			Х		С			1		2						r
					x			n		n				…		n
					1			11		12						1r
						x2		n21		n22				…		n2r
						…		…		…				…		…
						xs		ns1		ns2				…		nsr

Требуется провести регрессионно-корреляционный анализ статистических данных по следующей схеме:

1.Найти групповые средние yi переменной Y.

2.В прямоугольной системе координат построить точки xi;yi и

ломаную линию регрессии Y на Х. Согласно виду эмпирической

120

линии регрессии («ломаной») Y по X выбрать вид корреляционной связи между переменными Х и Y.

3.Найти генеральные средние x и y .

4.Составить уравнения линейной регрессии Y на Х и Х на Y. Построить графики регрессии.

5.По выбранному значению переменной X сделать прогноз ожидаемого среднего значения переменной Y.

6.Установить тесноту связи между переменными величинами X и

7.Оценить существенность выборочного коэффициента корреляции.

Вариант 1

X\Y				4	6				8	10			12
10				1	1				Д		–		–
10				1	1				–		–		–
15				1	1				–		–		–
20				2	4				2		–		–
25				–	5			А		И–			–
25				–	5				11	И–			–
30				–	6				12	10			–
35				–	4				10	10			8
40				–		–			–	6			6
				и			Вариант 2
							Вариант 2

X\Y		50			150				250		350		450
8		С			б–				1		2		1
8			–		б–				1		2		1
8,5			–		3				10		1		–
9		3			40				2		–		–
9,5		5			20				1		–		–
10		10			1				–		–		–
							Вариант 3

X\Y	9,9			10		10,1			10,2	10,3		10,4	10,5
0,8	1			2			–		–		–	–	–
0,9	–			1			2		1		–	–	–
1	–			–			2		2	1		–	–
1,1	–			–			–		1		–	3	–
1,2	–			1			–		–		–	–	2
1,3	–			–			–		–		–	–	1

121

Вариант 4

X\Y	16	26	36	46	56
20	4	–	–	–	–
25	6	8	–	–	–
30	–	10	32	4	–
35	–	–	3	12	1
40	–	–	9	6	5

Вариант 5

X\Y	1				3							5		7				9
20	8				12							–				–				–
30	2				20							–				–				–
40	–				8						10			9				10
50	–					–						1		8				12
							Вариант 6						И
							Вариант 6

X\Y	34			35					36				37				38			39
15	1			2						–	Д						–			–
15	1			2						–			–				–			–
17	3			6						4			–				–			–
19	–			4					А				15				–			–
19	–			4					13				15				–			–
21	–			1					11				4				8			2
23	–			–						1			2				5			2
25	–			б						3			5				4			7
25	–			1						3			5				4			7
27	–			–						–			–				3			1
29	–	и								–			–				1			1
29	–			–						–			–				1			1
							Вариант 7
X\Y	С						20-25					25-30			30-35			35-40
X\Y	10-15	15-20					20-25					25-30			30-35			35-40
0-0,2	4		–						–				–			–				–
0.2-0,4	2	2							–				–			–				–
0,4-0,6	–		–				2						–			–				–
0,6-0,8	–	6							–				4		4					–
0,8-1,0	–		–						–				–		6			6
1,0-1,2	–		–						–				–			–		4
							Вариант 8

X\Y	12			18				24					30				36		42
20	2			5						–			–				–			–
30	4			6						3			–				–			–
40	–			2						8			9				3			–
50	–			–				12					16				2			–
60	–			–						2			6				4		1
70	–			–						–			–				7		2
80	–			–						–			–				1		6

122

Вариант 9

X\Y	10	15	20	25	30	35
50	2	2	–	–	–	–
60	2	4	5	6	4	–
70	–	2	7	12	10	4
80	–	–	–	10	10	6
90	–	–	–	8	–	6

Вариант 10

X\Y	10		14	18				22			26		30	34		38		42
25	4		9	3					–		–		–		–	–		–
45	1		3	18				13			4		–		–	–		–
65	1		1	1				20			3		–		–	–		–
85	–		3	1				1			16		9		–	–		–
105	–		–	–				4			2		И			–		–
105	–		–	–				4			2		26		–	–		–
125	–		–	–					–		–		3	18		7		–
145	–		–	–					–		–		–	10		17		2
											Д
							Вариант 11
X\Y		55-115		115-175					А				235-295		295-355		355-415
X\Y		55-115		115-175					175-235				235-295		295-355		355-415
0-20		5			10					3			–		–			–
20-40		2			18				10				1		–			–
40-60			–		4	б							10		3			–
40-60			–		4			21					10		3			–
60-80			–		–					1			5		2			–
80-100			–	и						–			2		1		2
80-100			–		–					–			2		1		2
							Вариант 12
X\Y			С		2					3			4		5		6
X\Y		1			2					3			4		5		6
1		2			1					–			–		–			–
2		1			2					–			–		–			–
3			–		3					1			–		–			–
4			–		1					3			1		–			–
5			–		–					2			2		2		1
6			–		–					–			1		1		1
							Вариант 13

X\Y		6-6,8				6,8-7,6					7,6-8,4			8,4-9,2			9,2-10
16-20			–				–					–		1			3
20-24			–				–					–		9			7
24-28			–				4				8			20			2
28-32			–			10					19			1				–
32-36		2					3				8				–			–
36-40		2					1					–			–			–

123

Вариант 14

X\Y	1	3	5	7	9
20	–	12	8	–	–
30	2	10	–	–	–
40	–	6	10	9	10
50	–	–	2	8	12

Вариант 15

X\Y	0-100	100-200			200-300			300-400	400-500		500-600
0-100	–	–				–		1		2	–
100-200	–	–				2		1		–	2
200-300	2	8				4		–		–	–
300-400	3	21				3		1		–	–
400-500	8	26				5		1		–	1
500-600	–	14				9		И		1	–
500-600	–	14				9		1		1	–
				Вариант 16
X\Y	2,7-3,2	3,2-3,7					Д		4,7-5,2		5,2-5,7
X\Y	2,7-3,2	3,2-3,7			3,7-4,2			4,2-4,7	4,7-5,2		5,2-5,7
2-2,6	–	–				–		–		6	2
2,6-3,2	–	–			А			1		8	–
2,6-3,2	–	–				–		1		8	–
3,2-3,8	–	–				2		13		1	–
3,8-4,4	–	1				6		20		–	–
4,4-5	1	1	б					3		–	–
4,4-5	1	1			16			3		–	–
5-5,6	3	3				4		–		–	–
5,6-6,2	3	и				–		–		–	–
5,6-6,2	3	3				–		–		–	–

		Вариант 17
X\Y	С	10-20	20-30	30-40	40-50
X\Y	0-10	10-20	20-30	30-40	40-50
15-18	2	–	–	–	–
18-21	4	3	–	–	–
21-24	–	5	5	3	3
24-27	–	–	30	10	4
27-30	–	–	20	7	4

Вариант 18

X\Y	11,8-12,2	12,2-12,6	12,6-13	13-13,4	13,4-13,8	13,8-14,2
13,8-14,2	2	1	–	–	–	–
14,2-14,6	5	1	–	–	–	–
14,6-15	–	6	2	–	–	–
15-15,4	–	1	2	1	–	–
15,4-15,8	–	–	6	3	1	–
15,8-16,2	–	–	–	4	4	3
16,2-16,6	–	–	–	–	2	6

124

Вариант 19

X\Y	50	150	250	350	450
10	–	1	2	–	1
20	–	3	8	1	–
30	3	30	4	–	–
40	5	20	1	–	–
50	10	10	–	–	–

Вариант 20

X\Y	1200-1300			1300-1400				1400-1500				1500-1600			1600-1700
40-45		1			–			–					–				–
45-50		3		2				3					–				–
50-55		2		4				4					3				–
55-60		–		4				5					6		2
60-65		–			–			3	И						2
60-65		–			–			3					4		2
65-70		–			–			–					–		2
								Д
					Вариант 21
X\Y	9,9		10		10,1			10,2			10,3			10,4			10,5
0,8	–		2			А						–		–			–
0,8	–		2			1		–				–		–			–
0,9	1		1			2		–				–		–			–
1	–		–			2		2			1			–			–
1,1	–		–		б			1				–		3			–
1,1	–		–			–		1				–		3			–
1,2	–		–			1		–				–		–			2
1,3	–		и			–		–				–		1			–
1,3	–		–			–		–				–		1			–
					Вариант 22
X\Y		С					1,6-2,4		2,4-3,2				3,2-4			4-4,8
X\Y		0-0,8		0,8-1,6			1,6-2,4		2,4-3,2				3,2-4			4-4,8
0,16-0,22		4		–				–		–				–			–
0,22-0,28		4		6				–		–				–			–
0,28-0,34		–		10				8		–				–			–
0,34-0,4		–		3				15	2					–			–
0,4-0,46		–		–				10	20					4			–
0,46-0,52		–		–				4	5					–			–
0,52-0,58		–		–				–	2					1			–
0,58-0,64		–		–				–		–				–		2
					Вариант 23

X\Y		18		28				38					48		58
20		–		3				–					–				–
25		4		5				–					–				–
30		–		10				30					4				–
35		–		3				–					12		1
40		–			–			8					6		5

125

Вариант 24

X\Y	5-7	7-9	9-11	11-13	13-15
0,25-0,75	6	1	–	–	–
0,75-1,25	12	4	–	–	–
1,25-1,75	–	18	16	5	–
1,75-2,25	–	4	14	5	2
2,25-2,75	–	–	2	5	3
2,75-3,25	–	–	–	–	3

Вариант 25

X\Y		3	5		7	9	11
10		–	1		1	–	–
15		1	1		–	–	–
20		2	4		2	–	–
25		–	4		11	–	–
30		–	6		12	10	–
35		–	4		10	10	8
40		–	–		Д	–	6
40		–	–		6	–	6
				А
	4.6. Образец для выполнения расчетнойИработы

«Корреляционно-регрессионный анализ статистических данных для cгруппированной выборки»

Получены		результаты на людений				двумерной		случайной
величины (X; Y):

X\Y	С			б60	70		80	90
X\Y		50		б60	70		80	90
10		2		2	–		–	–
			и
15		2	4		2		–	–
20		–		5	7		–	–
25		–		6	12		10	8
30		–		4	10		10	–
35		–		–	4		6	6

Провести регрессионно-корреляционный анализ статистических данных.

Решение.

1. Вычислим частоты ni	r		s
1. Вычислим частоты ni	nij	и nj nij и внесем их в
	j 1		i 1
корреляционную табл. 4.14.	Для каждого		значения xi найдем

126

				r
				yjnij
групповые средние	y	переменной Y по формуле	y	j 1	, где
групповые средние	y	переменной Y по формуле	y		, где
	i		i	ni
				ni

nij – частоты пар (xi; yj ) и ni nij .

											j 1
Если x=10, то			y				50 2 60 2					55.
Если x=10, то			y									55.
			1							4
Если x=15, то			y	2				50 2 60 4 70 2					60.
Если x=15, то			y	2									60.
											8
Если x=20, то			y						60 5 70 7			65,8.
Если x=20, то			y									65,8.
				3						12
				6						12				И
Если x=25, то			y	4			60 6 70 12 80 10 90 8									75,5.
Если x=25, то			y	4												75,5.
											36
												Д
Если x=30, то			y				60 4 70 10 80 10							72,5.
			5								24
Если x=35, то			y					70 4 80 6 90 6					78,5.
Если x=35, то			y										78,5.
											16
Вычисленные						групповые						средние					yi	поместим				в
										б
корреляционную табл. 4.14.																		Таблица 4.14
					и
									КорреляционнаяАтаблица
									КорреляционнаяАтаблица
X\Y		50				60					70	80			90			ni			yi
10		2				2					–	–			–			4	55
15		2				4					2	–			–			8	60
20		–				5					7	–			–			12	65,8
25		–				6					12	10			8			36	75,5
30		–				4					10	10			–			24	72,5
		С
35		– –									4	6			6			16	78,5
nj		4				21					35	26			14			100			–
2.	В прямоугольной системе координат строим точки xi;																			yi		и

ломаную линию регрессии Y на Х (рис. 4.5).

127

90
80
70
60
50
40
30
20
10
0
10	15	20	25	30	35

Рис. 4.5. Эмпирическая линия регрессии Y на X

Согласно виду эмпирической линии регрессии Y на X выбираем линейную связь между переменными Х и Y.

3. Находим генеральные средние x и y :

xini

10 4 15 8 20 12 25 36 30 24 35 16

i 1

25,8;

100

yjnj

j 1

50 4 60 21 70 35 80 26 90 14

72.

100

Составим

уравнен еАлинейной

регрессии

на Х:

yx (x

Y на Х по

Определим

формуле

коэфф ц ент

регрессии

x y

, где

2 2

– выборочная дисперсия по Х.

x x

SX2

xi ni

12 25

i 1

4 15 8 20

36 30

. 24 35

707;

100

SX2

707 25,82

707 665,24 41,36;

xi yjnij

10 5 2 15 2 50 ... 35 6 90

i 1

j 1

1909;

100

x y 25,8 72,5 1870,5;

128

1909 1870,5

0,93– значение коэффициента регрессии Y на Х.

41,36

Имеем уравнение регрессии Y на Х: yx

72,5 0,93(x 25,8)

или

0,93x 48,51.

Находим

уравнение

линейной

регрессии

на

xy(y

Х на

Определим

коэффициент регрессии

по

формуле

x y

2 – выборочная дисперсия по Y.

;

y2n

j 1

502

4 602 21 702 35 802

26 902

5369;

100

5369 72,52

5369 5256,25 112,75;

1909 1870,5

0,34 – значение коэффициента регрессии Х на Y.

112,75

Имеем уравнение регрессии Х на Y:

xy 25,8 0,34(y 72,5)

или

xy 0,34y 1,15

Построим графики регрессии (рис. 4.6). Для построения графиков

регрессии составим табл цы значений:

1) y

0,93x

48,51:

yх

57,8

76,41

2) xy 0,34y 1,15:

xу

26,03

84,8

5. По уравнениям регрессии сделаем прогнозы ожидаемых средних значений по переменным Х и Y: если х=25,8, то y 76,41; если y=90, то x 28,3.

129

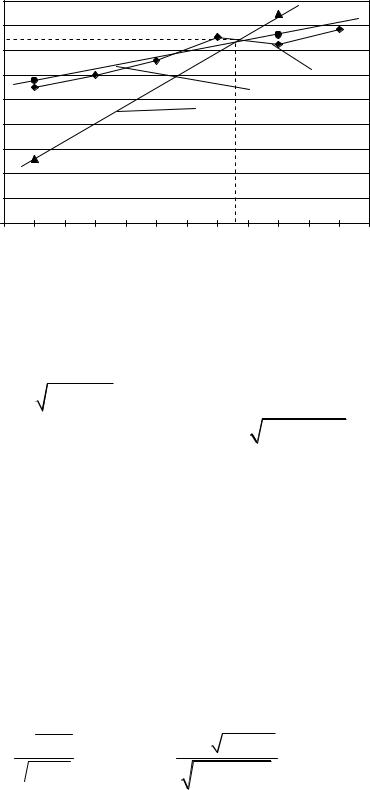
90
80
70
60					1
60				2
50				2
50			3
			3
40
30
20
10
0
10	15	20	25	30	35

Рис. 4.6. Прямые регрессии: 1 – эмпирическаяИлиния регрессии Y на Х;

2 – теоретическая линия регрессии Y на Х;

3 – теоретическая линия регрессии Х на Y

6. Для установления тесноты связи между переменными величинами X и Y вычислим выборочный коэффициент корреляции

по формуле r yx xy .

на прямо пропорц ональнуюбзависимость, то есть с возрастанием значений, например, X значен я Y также будут возрастать. Графики уравнений регрессии также подтверждают этот вывод.

Так как	yx	0,93;	xy	0,34	, то r	0,93 0,34 0,56.
					Д
По шкале Чеддока корреляционная связь между X и Y является
		и					линейными уравнениями
заметной и ее можно оп сать полученнымиА

регрессии. Полож тельный знак коэффициента корреляции указывает С

7. Оценим существенность выборочного коэффициента корреляции.

Так как имеем выборку небольшого объема, то для оценки

существенности выборочного коэффициента корреляции для проверки основной гипотезы H0 в пользу отсутствия линейной корреляционной связи между величинами Х и Y используем

статистику t rn 2 . Имеем t 0,56100 2 6,6.

1 r2 1 (0,56)2

Статистика имеет распределение Стьюдента с k=100–2=98 степенями свободы. Зададимся уровнем значимости 0,05 и по прил. 3 найдем критическое значение tкр=t1-0,05;98=1,99.

130

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 1920 / 2120 21 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
07.01.2021333.26 Кб2183.pdf
#
07.01.20211.92 Mб11830.pdf
#
07.01.20211.93 Mб21831.pdf
#
07.01.20211.93 Mб211832.pdf
#
07.01.20211.93 Mб41833.pdf
#
07.01.20211.93 Mб951834.pdf
#
07.01.20211.94 Mб21835.pdf
#
07.01.20211.94 Mб21836.pdf
#
07.01.20211.94 Mб41837.pdf
#
07.01.20211.95 Mб241838.pdf
#
07.01.20211.95 Mб01839.pdf

X\Y	16	26	36	46	56
20	4	–	–	–	–
25	6	8	–	–	–
30	–	10	32	4	–
35	–	–	3	12	1
40	–	–	9	6	5

X\Y	10	15	20	25	30	35
50	2	2	–	–	–	–
60	2	4	5	6	4	–
70	–	2	7	12	10	4
80	–	–	–	10	10	6
90	–	–	–	8	–	6

X\Y	50	150	250	350	450
10	–	1	2	–	1
20	–	3	8	1	–
30	3	30	4	–	–
40	5	20	1	–	–
50	10	10	–	–	–

X\Y	16	26	36	46	56
20	4	–	–	–	–
25	6	8	–	–	–
30	–	10	32	4	–
35	–	–	3	12	1
40	–	–	9	6	5

X\Y	10	15	20	25	30	35
50	2	2	–	–	–	–
60	2	4	5	6	4	–
70	–	2	7	12	10	4
80	–	–	–	10	10	6
90	–	–	–	8	–	6

X\Y	50	150	250	350	450
10	–	1	2	–	1
20	–	3	8	1	–
30	3	30	4	–	–
40	5	20	1	–	–
50	10	10	–	–	–

X\Y	16	26	36	46	56
20	4	–	–	–	–
25	6	8	–	–	–
30	–	10	32	4	–
35	–	–	3	12	1
40	–	–	9	6	5

X\Y	10	15	20	25	30	35
50	2	2	–	–	–	–
60	2	4	5	6	4	–
70	–	2	7	12	10	4
80	–	–	–	10	10	6
90	–	–	–	8	–	6

X\Y	50	150	250	350	450
10	–	1	2	–	1
20	–	3	8	1	–
30	3	30	4	–	–
40	5	20	1	–	–
50	10	10	–	–	–