Файловый архив студентов. Файловый архив студентов.
1301 вуз, 5072 предмет.
/ Регистрация
FAQ Обратная связь Вопросы и предложения
Добавил:
Опубликованный материал нарушает ваши авторские права? Сообщите нам.
Вуз:
Сибирская государственная автомобильно-дорожная академия
Предмет:
[НЕСОРТИРОВАННОЕ]
Файл:
1834.pdf
Скачиваний:
95
Добавлен:
07.01.2021
Размер:
1.93 Mб
Скачать
☆
►Содержание►

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Окончание табл. 4.9

1

 

 

2

3

 

 

Нахождение уравнений

4.2

 

y

x 5,4 1,8(x 3,2) или

y

x 1,8x 0,36;

регрессии

 

 

x

y 3,2 0,32(y 5,4) или

 

y

x

y

yx(x

x

);

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

xy 0,32y 1,472

 

x

y

x

xy(y

y

)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Нахождение коэффициента

4.3

r

 

 

 

 

 

0,576 X и Y связаны

1,8 0,32

корреляции r

 

прямой корреляционной зависимостью

 

 

 

 

 

 

 

 

Проверка значимости r

4.3

H0: r 0:

 

t

 

2,98; t0,95;18 2,1;

 

 

 

 

 

 

 

 

 

 

2,98 2,1 гипотеза H0 отвергается,

 

 

 

 

 

 

 

 

т.е. между переменными присутствует

 

 

 

 

 

 

 

 

линейная корреляционная связь

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

И

 

 

 

 

 

 

 

 

 

Корреляционное отношение и его свойства

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Д

 

 

 

 

 

 

 

 

Коэффициент корреляции применим лишь в случае линейной

зависимости между переменными X и Y . ля оценки тесноты связи

между величинами X и Y при любой форме зависимости применяют

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

А

 

 

 

 

 

 

 

 

 

 

 

показатель – корреляционное отношение.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

б

 

 

 

 

 

 

 

 

 

межгр2

ост2 ,

 

 

Рассмотрим правило сложения дисперсий: общ2

где общ2

– общая дисперсия, характеризующая влияние величины Х и

 

 

 

 

 

 

 

 

 

 

и

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

случайных

факторов на вариацию Y;

межгр

–

межгрупповая

 

 

 

 

 

 

С

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

дисперсия, характер зующая воздействие величины Х на вариацию Y;

ост2

– остаточная д сперс я, которой измеряют влияние неучтенных

факторов на Y, не зависящих от Х (табл. 4.10).

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Корреляционное отношение и его свойства

Таблица 4.10

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Понятия

 

 

 

 

 

 

 

Код

 

 

 

 

 

Задание

 

 

 

 

 

 

 

 

 

 

1

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

3

 

 

 

Корреляционное отношение yx величины

4.4

 

По данным из табл. 4.9

Y по X – отношение

межгруппового

 

 

 

найти

 

 

корреляционное

 

 

 

отношение yx.

 

 

 

среднего

квадратического

отклонения к

 

 

 

 

 

 

общему

среднему

 

 

квадратическому

 

 

 

Решение.

 

 

 

 

отклонению признака Y , т.е.

 

 

 

 

 

 

 

 

 

2

 

1

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

x

 

((1 5,4)

 

4

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

20

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

y

 

 

 

межгр

 

 

y

 

 

(

y

xi

 

y

)2 nXi

/ n

,

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

x

 

 

 

 

(5,4 5,4)2 10

 

 

 

yx

 

 

 

 

 

 

 

(yj

 

 

 

 

/ n

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

общ

 

y

 

y

)2 nYj

 

 

 

 

(8,3 5,4)2 6) 6,395;

104

Окончание табл. 4.10

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

3

 

 

где

y

xi ,

 

 

 

y

– условная

и

общая

средние

 

 

 

 

y

 

2,52;

 

 

признака

 

 

 

 

Y ;

yx2

–

коэффициент

 

 

 

 

x

1

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

((1 5,4)

2

6

детерминации, показывает, какая часть

 

 

y

20

 

 

 

 

 

 

 

 

 

 

общей вариации Y обусловлена вариацией Х.

 

 

(5 5,4)2 6

 

 

Аналогично

определяется

корреляционное

 

 

(9 5,4)2 8) 11,04;

отношение xy величины X по Y

 

 

 

 

 

 

 

 

y

3,32;

 

 

 

 

Свойства корреляционного отношения:

 

 

 

 

 

 

1.

0 yx

 

1.

 

 

 

 

 

 

 

 

yx

 

 

2,52

 

0,76

 

2. yx 0

 

 

 

корреляционной связи нет.

 

 

 

3,32

 

3.

yx 1

 

зависимость

Y

от X

 

 

степень

корреляционной

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

зависимости Y

от X

функциональная.

 

 

 

 

 

 

 

 

И

 

 

 

4. yx

r

.

 

 

 

 

 

 

 

 

 

высокая.

 

 

 

5. yx

 

r

 

 

между X и Y

 

 

Д

нации yx2

 

 

 

 

 

 

существует

 

0,58

, т.е. 58 %

 

 

 

 

 

 

линейная корреляционная зависимость.

 

 

 

изменения

Y

 

вызваны

6.

 

yx

xy ,

т.е.

при

вычислении

 

изменением Х

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

А

 

 

 

 

 

 

 

 

 

 

 

 

 

корреляционного отношения важно знать,

 

 

 

 

 

 

 

 

 

 

 

 

 

какую переменную считать зависимой

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

б

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

и

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

4.2. Задания в тестовой форме

 

 

 

 

 

 

 

 

Элемент 4.1. Зав с мости между случайными величинами

 

 

 

 

 

 

 

 

 

 

 

С

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Задание 1.

(Выбер те од н вариант ответа)

 

 

 

 

 

 

 

Зависимость между переменными называется статистической, если изменение величины Х влечет за собой…

Варианты ответа: 1) определенное изменение величины Y; 2) изменение распределения величины Y; 3) изменение среднего значения величины Y.

Задание 2. (Выберите один вариант ответа)

Зависимость между переменными называется корреляционной, если каждому значению факторного признака соответствует…

Варианты ответа: 1) вполне определенное неслучайное значение результативного признака; 2) множество значений результативного признака, т.е. определенное статистическое распределение; 3) целое распределение значений результативного признака; 4) строго определенное значение факторного признака.

105

Задание 3. (Выберите один вариант ответа)

Корреляционная зависимость называется регрессионной, если каждому значению случайной величины Х соответствует …

Варианты ответа: 1) средняя величина распределения

случайной

величины Y; 2)

дисперсия

случайной

величины

Y;

3) среднее

квадратическое

отклонение

случайной

величины

Y;

4) определенное значение случайной величины Y.

 

 

Задание 4. (Выберите один вариант ответа)

Задачей регрессионного анализа является… Варианты ответа: 1) определение формы связи между

факторным и результативным признаками; 2) установление тесноты связи между факторным и результативным признаками; 3) вычисление ошибки показателя теснотыИсвязи; 4) определение доверительного интервала для показателя тесноты связи.

Задание 5. (Выберите один вариант ответа)

Определение тесноты связи между факторным Х и результативным Y признаками – это задача …

Варианты ответа: 1) регрессионного анализа; 2) выборочного

метода; 3) корреляционного

анализа; 4) метода наименьших

квадратов.

б

Д

 

 

Задание 6. (Выберите один вариант ответа)

 

и

Аэто зависимость, при которой

Парная корреляц я –

результативный пр знак Y зав

сит от…

ВариантыСответа: 1) двух факторных признаков; 2) множества факторных признаков; 3) совокупности пар; 4) одного факторного признака Х.

Задание 7. (Выберите один вариант ответа)

По направлению различают статистические связи … Варианты ответа: 1) прямые и обратные; 2) возрастающие и

убывающие; 3) прямолинейные; 4) умеренные.

Задание 8. (Выберите один вариант ответа)

По аналитическому выражению связи в математической статистике квалифицируют на …

Варианты ответа: 1) сильные и слабые; 2) прямые и обратные; 3) закономерные и произвольные; 4) линейные и криволинейные.

106

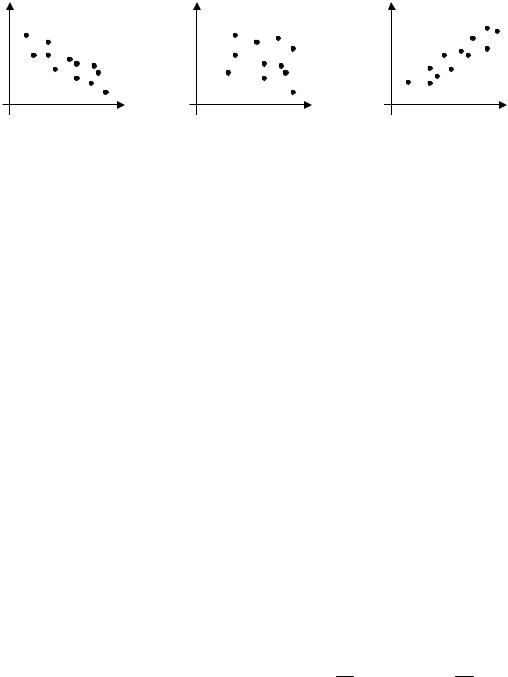
Задание 9. (Выберите ответы согласно тексту задания)

Установите по виду корреляционного поля тип зависимости между переменными.

y

y

y

1)

 

2)

 

 

3)

x

 

 

 

 

Варианты ответа: a) зависимость между переменными

отсутствует;

b)

обратная

зависимость между

переменными;

c) прямая зависимость между переменными.

 

 

 

 

 

 

И

 

Задание 10. (Выберите один вариант ответа)

 

Степень

тесноты

корреляционной связи можно измерить с

помощью: …

 

 

 

 

Д

 

 

 

 

 

 

 

Варианты

ответа:

 

1) коэффициента

корреляции;

2) коэффициента

вариации;

3) коэффициента

регрессии;

4) коэффициента асимметрии.

 

 

 

 

 

 

б

 

 

 

 

Элемент 4.2. Уравнение регрессии

 

 

 

и

Ан вариант ответа)

 

Задание 11. (Выбер те од

 

Уравнение регресс

связывает значения факторного признака с

…

С

 

 

 

 

 

 

 

 

 

 

Варианты ответа: 1) определенным значением результативного признака; 2) максимальным значением результативного признака; 3) средним значением результативного признака; 4) дисперсией результативного признака.

Задание 12. (Выберите ответы согласно тексту задания)

Установите соответствие между аналитическим представлением и видами корреляционной зависимости:

a) f (x); b) график функции g (y); c) xy g (y); d) yx f (x). Варианты ответа: 1) выборочная регрессия Y на Х; 2) выборочное уравнение регрессии Х на Y; 3) выборочная линия

регрессии Х на Y; 4) выборочное уравнение регрессии Y на Х.

107

Задание 13. (Выберите один вариант ответа)

Методу наименьших квадратов соответствует формула…

n

2

 

n

2

 

Варианты ответа: 1) yi

yx

 

max; 2)

yi

yx

 

min;

n

3) yi yx min ; 4)

i 1

i 1

n

yi yx min.

i 1 i 1

Задание 14. (Выберите один вариант ответа)

При применении метода наименьших квадратов к линейному уравнению регрессии минимизируется сумма квадратов...

Варианты ответа: 1) коэффициентов регрессии; 2) отклонений значений зависимой переменной; 3) отклонений эмпирических значений зависимой переменной от значений, найденных по уравнению регрессии; 4) остаточных членов.

Задание 15. (Выберите один вариант ответа)

Если при равномерном возрастании факторного признака средние

изменении фактора на 1 ед н цу; 2) на сколько процентов изменится в среднем результат, если фактор изменится на 1 %; 3) среднее изменение фактора при изменении результата на 1.

значения результативного признака равномерно возрастают, то

уравнение регрессии ищется в виде…

И

Варианты ответа: 1) линейного уравнения; 2) уравнения

гиперболы; 3) уравнения параболы; 4) уравнения третьей степени.

 

 

 

Д

Задание 16. (Выберите один вариант ответа)

Параметр

а в уравнен

Апарной

линейной регрессии y=ax+b

показывает…

 

ответа:б1) среднее изменение результата при

Варианты

 

 

и

 

 

 

С

 

 

Задание 17. (Выберите один вариант ответа)

Коэффициент регрессии в линейной регрессии совокупного спроса на мобильные телефоны (в тысячах рублей) по цене (в рублях) оказался равным 1. Это означает…

Варианты ответа: 1) увеличение цены на 1 % снижает спрос на мобильные телефоны на 1 %; 2) увеличение цены на 1 рубль снижает спрос на мобильные телефоны на 1 %; 3) увеличение цены на 1 % снижает спрос на мобильные телефоны на 1 тысячу рублей; 4) увеличение цены на 1 рубль снижает спрос на мобильные телефоны на 1 тысячу рублей.

108

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
Помощь Обратная связь Вопросы и предложения Пользовательское соглашение Политика конфиденциальности