
- •Введение
- •КОДИФИКАТОР РАЗДЕЛА «МАТЕМАТИЧЕСКАЯ СТАТИСТИКА»
- •ВВЕДЕНИЕ В МАТЕМАТИЧЕСКУЮ СТАТИСТИКУ
- •Предельные теоремы теории вероятностей
- •Основные законы распределения непрерывных случайных величин
- •Законы распределения случайных величин, связанные с нормальным распределением
- •Глава 1. ВЫБОРКИ И ИХ ХАРАКТЕРИСТИКИ
- •1.1. Справочный материал
- •Задачи математической статистики
- •Основные понятия математической статистики
- •Графическое изображение статистического ряда распределения
- •Эмпирическая функция распределения
- •Числовые характеристики статистического ряда
- •Моменты случайных величин
- •1.2. Задания в тестовой форме
- •Элемент 1.1. Статистическое распределение выборки
- •Элемент 1.2. Основные числовые характеристики выборки
- •Элемент 1.3. Дополнительные числовые характеристики выборки
- •1.3. Варианты заданий для расчетной работы «Первичная обработка статистических данных»
- •1.4. Образец для выполнения расчетной работы «Первичная обработка статистических данных»
- •Глава 2. ЭЛЕМЕНТЫ ТЕОРИИ ОЦЕНОК
- •2.1. Справочный материал
- •Понятие статистической оценки и ее свойства
- •Точечные оценки и их нахождение
- •Выравнивание статистического ряда
- •Интервальные оценки
- •2.2. Задания в тестовой форме
- •Элемент 2.1. Точечные оценки
- •Элемент 2.2. Интервальные оценки
- •2.4. Образец для выполнения расчетной работы «Выравнивание статистических рядов»
- •Глава 3. ПРОВЕРКА СТАТИСТИЧЕСКИХ ГИПОТЕЗ
- •3.1. Справочный материал
- •Понятие статистической гипотезы и ее виды
- •Критическая область и ее нахождение
- •Проверка параметрических гипотез
- •3.2. Задания в тестовой форме
- •Элемент 3.1. Статистические гипотезы
- •Элемент 3.2. Ошибки проверки статистических гипотез
- •Элемент 3.3. Критическая область
- •Элемент 3.4. Проверка статистических гипотез
- •3.3. Варианты заданий для расчетной работы «Проверка гипотезы о равенстве генеральных дисперсий»
- •3.5. Варианты заданий для расчетной работы «Проверка гипотезы о законе распределения генеральной совокупности по критерию Пирсона»
- •4.1. Справочный материал
- •Зависимости между случайными величинами
- •Корреляционное поле
- •Линейная парная регрессия
- •Нелинейная парная регрессия
- •Коэффициент корреляции и его свойства
- •Проверка значимости коэффициента корреляции
- •Корреляционная таблица
- •Корреляционное отношение и его свойства
- •4.2. Задания в тестовой форме
- •Элемент 4.2. Уравнение регрессии
- •Элемент 4.3. Коэффициент корреляции
- •Элемент 4.4. Корреляционное отношение
- •4.3. Варианты заданий для расчетной работы «Подбор уравнения регрессии для бесповторной выборки»
- •4.4. Образец для выполнения расчетной работы «Подбор уравнения регрессии для бесповторной выборки»
- •Библиографический список
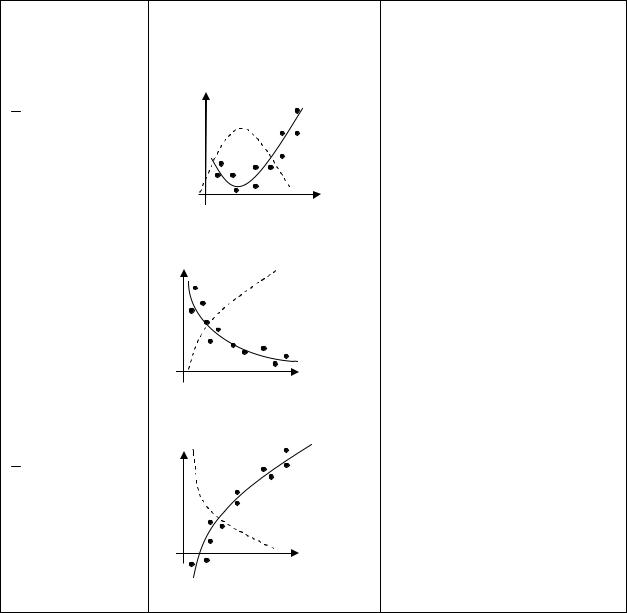
Нелинейная парная регрессия
В случае, когда соотношения между переменными нельзя выразить линейной функцией, используют уравнения нелинейной регрессии. Наиболее часто встречаются следующие виды нелинейной зависимости: полиномиальная, гиперболическая, логарифмическая, показательная. Неизвестные параметры этих зависимостей также находят исходя из метода наименьших квадратов (табл. 4.5).
Таблица 4.5
Системы нормальных уравнений для определения параметров нелинейной парной регрессии
Вид зависимости |
|
Корреляционное поле |
|
Система нормальных |
|
|
||||||||||||||
|
|
|
|
уравнений |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
1 |
|
|
|
2 |
|
|
|
И |
|
3 |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Квадратичная |
|
|
|
|
|
|
|
a x4 |
b x3 |
c x2 |
x2y ; |
|||||||||
зависимость |
|
|
|
|
|
|
Д |
i |
|
|
i |
i |
|
i i |
||||||
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
x ax2 bx c |
|
|
|
a 0 |
a 0 |
a xi3 b xi2 c xi |
xi yi; |
||||||||||||
|
|
|
|
|
|
|
|
|
А |
a x2 b x cn y |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
i |
|
|
i |
|
i |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Гиперболическая |
|
и |
|
|
|
Приводят |
|
|
уравнение |
|
к |
|||||||||
|
|
|
|
|
|
|
|
|
||||||||||||
зависимость |
|
y |
|
|
a 0 |
|
|
линейной |
|
зависимости |
|
с |
||||||||
|
|
|
a |
С |
б |
|
|
помощью подстановки u |
1 |
: |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
yx x b |
|
|
|
|
|
x |
|||||||||||||
|
|
|
|
|
|
|
2 |
b ui |
uiyi; |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
a ui |
|
|
||||||
|
|
|
|
|
|
|
|
|
a 0 |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
a u nb y |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
x |
|
|
|
i |
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Логарифмическая |
|
|
|
|
|
|
Приводят |
|
|
уравнение |
|
к |
||||||||
зависимость |
|
y |
|
|
|
|
|
линейной зависимости с помо- |
||||||||||||
|
y |
x alnx b |
|
|
|
|
a 0 |
щью подстановки u ln x |
|
|
||||||||||
a 0 x
99

Окончание табл. 4.5
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
||||
Показательная |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Для |
|
линеаризации |
показа- |
||||||||||||||||||||||||||||
зависимость |
|
|
|
|
|
|
|
|
|
|
y |
|
|
a 1 |
|
тельной зависимости приме- |
|||||||||||||||||||||||||||||||
|
y |
|
|
b ax |
|
|
|
|
|
|
|
|
|
|
0 a 1 |
|
|
|
|
|
няют процесс логарифмиро- |
||||||||||||||||||||||||||
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b 0 |
|
|
|
|
|
|
|
|
вания: |
lg |
y |
x |
lgb ax , |
откуда |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lg |
y |
x |
|
xlga lgb. |
|
|
Пусть |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
A lga; B lgb; |
|
Y lg |
y |
x , |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
тогда |
получим |
|
линейную |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
зависимость Y Ax B |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Коэффициент корреляции и его свойства |
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
Коэффициент корреляции r – показатель тесноты линейной связи |
||||||||||||||||||||||||||||||||||||||||
между |
величинами |
X |
|
и |
Y , |
который |
оценивается |
по |
|
величине |
|||||||||||||||||||||||||||||||||||||
рассеяния |
|
|
|
|
значений |
|
|
одной |
переменной |
|
|
|
вокруг |
|
среднего |
||||||||||||||||||||||||||||||||
арифметического другой (табл. 4.6). |
|
И |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 4.6 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Нахождение и свойства коэффициента корреляции |
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Нахождение |
|
|
|
|
Код |
|
|
|
|
|
|
|
Задание |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Д |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
– средняя |
|
|
|
|
|
|
Выборочное |
уравнение |
||||||||||||||||||||
|
|
r |
|
yx xy |
геометрическая |
4.3 |
|
|
|||||||||||||||||||||||||||||||||||||||
коэффициентов регрессии. |
|
Вы ирается |
знак |
|
|
|
|
парной регрессии имеет |
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
вид y 3,4 0,7x , |
||||||||||||||||||||||||||||||||||||||||||
«+», если |
|
yx |
0; |
xy |
0, |
|
|
|
А |
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
знак |
«–», |
если |
|
|
|
|
X 2; |
Y 2,4. |
Найти |
|||||||||||||||||||||||||||||||||||
|
yx |
0; |
|
|
|
xy |
0. |
Наход тся |
|
з |
уравнений |
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
б |
|
|
|
|
|
коэффициент |
|
|
|
|
|
|||||||||||||||||
регрессии. |
|
|
|
|
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
корреляции. |
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
___ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение. Из уравнения |
|||||||||||||||||||||||
2) |
|
|
r |
xy |
x |
|
y |
|
или r |
yx |
|
SX |
|
находится по |
|
|
|
|
регрессии |
yx |
0,7, |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
S |
X |
S |
|
|
S |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
Y |
|
|
|
|
|
|
|
|
|
Y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
выборке, |
|
где |
SС, S – выборочные средние |
|
|
|
|
откуда |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X |
Y |
|
|
|
|
|
|
|
|
|
|
|
|
r 0,7 |
2 |
0,58 |
|||||||||||||
квадратические отклонения |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
2,4 |
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Свойства коэффициента корреляции: |
|
|
4.3 |
По результатам наб- |
||||||||||||||||||||||||||||||||||||
1) |
|
r |
|
1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
людений |
|
получены |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
уравнения |
|
регрессии |
|||||||||||
2) r 0 |
|
|
|
|
|
|
|
|
линейной |
|
корреляционной |
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
yx |
0,7x 5 |
|
|
|
|
и |
||||||||||||||||||||||||||||
зависимости нет. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
0,8y 18. |
Оцените |
||||||||||||||||||||||||||||||
3) |
|
r 0 |
|
связь между величинами прямая, |
|
|
|
|
|
y |
|||||||||||||||||||||||||||||||||||||
т.е. с ростом X увеличивается Y . |
|
|
|
|
|
|
|
тесноту |
связи |
между |
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
переменными X и Y . |
|||||||||||||
100

Окончание табл. 4.6
|
|
|
|
|
|
1 |
|
|
2 |
|
|
|
3 |
|
|
|
4) |
r 0 связь между величинами обратная, |
|
|
Решение. |
yx 0,7 |
и |
||||||||||
т.е. с ростом X убывает Y . |
|
|
xy 0,8. |
|
|
Тогда |
||||||||||
5) |
|
r |
|
1 X и Y связаны функционально |
|
|
|
|
||||||||
|
|
|
|
|||||||||||||
|
|
|
|
r |
|
|
|
|
|
|
||||||
|
|
|
|
|
0,7 0,8 |
0,75 1 |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
Шкала Чеддока для оценки силы связи |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
связь |
между |
||||||
|
|
|
|
|
коэффициента корреляции |
|
|
величинами |
прямая |
и |
||||||
|
|
|
|
|
Значение r |
Интерпретация |
|
|
|
|||||||
|
|
|
|
|
|
|
|
высокая |
|
|
|
|
||||
|
|
|
|
|
0 – 0,3 |
Очень слабая |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
0,3 – 0,5 |
Слабая |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,5 – 0,7 |
Средняя |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,7 – 0,9 |
Высокая |
|
|
|
|
|
|
|
|
|
|
При |
|
|
0,9 – 1 |
Очень высокая |
силы |
|
|
|
|
|
|
|
|
|
||
отрицательной |
корреляции значения |
|
И |
|
|
|
|
|
|
|||||||
связи меняют на противоположные |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
H |
|
Д |
|
|
|
|
|
|
|||
|
|
|
|
|
Проверка значимости коэффициента корреляции |
|
||||||||||
|
|
|
|
|
Так как коэффициент корреляции r |
вычисляется по значениям |
||||||||||
|
|
|
|
|
|
А |
выборку |
из |
генеральной |
|||||||
переменных, случайно попавших в |
||||||||||||||||
совокупности, то r – случайная величина. Обычно проверяется гипотеза 0 об отсутствии линейной корреляционной связи между
|
|
|
|
|
|
|
|
и |
|
|
|
т.е. |
H0 :r 0, |
где |
||||
переменными в генеральной совокупности, |
||||||||||||||||||
альтернативная гипотеза H1: r 0 (табл. 4.7). |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
С |
б |
|
|
|
|
Таблица 4.7 |
|||||
|
|
|
|
|
|
|
хема проверки значимости коэффициента корреляции |
|
||||||||||
|
|
|
|
|
|
|
Этапы |
|
|
|
|
Код |
|
|
Задание |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
2 |
|
|
3 |
|
|
|
1. Выбрать гипотезу H0 |
|
об |
4.3 |
Для проверки гипотезы на уровне |
||||||||||||||
отсутствии |
|
|
линейной |
|
корреля- |
|
значимости |
0,05 |
о наличии |
|||||||||
ционной связи между переме- |
|
линейной |
корреляционной |
связи |
||||||||||||||
нными в генеральной совокуп- |
|
между |
количеством |
выпускаемой |
||||||||||||||
ности, т.е. H0 :r 0 |
|
|
|
|
|
продукции и полными затратами на их |
||||||||||||
|
|
|
|
|
|
производство |
было |
обследовано 40 |
||||||||||
2. Выбрать статистику |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
однотипных предприятий. |
|
||||
t |
r |
n 2 |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
, |
которая |
имеет |
|
Наблюдаемое |
значение |
статистики |
||||||||||
|
|
|
|
|
|
|||||||||||||
1 r2 |
|
|||||||||||||||||
|
|
|
|
|
|
|
с |
|
tнаб 7,54. |
Найти |
|
критическое |
||||||
t-распределение Стьюдента |
|
значение статистики и сделать вывод |
||||||||||||||||
k n 2 степенями свободы |
|
|
|
|||||||||||||||
|
|
|
относительно существенности связи. |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
101
Окончание табл. 4.7
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
2 |
|
|
|
3 |
|
|
|
|
||||
3. |
|
|
Вычислить |
наблюдаемое |
|
|
Решение. |
Для |
|
уровня |
||||||||||||||||||
значение статистики критерия |
|
|
значимости 0,05 и числа степеней |
|||||||||||||||||||||||||
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
свободы |
k 40 2 38 |
находим |
|||||
|
tнаб |
|
|
|
|
|
|
|
n 2 |
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
критическое |
значение |
статистики |
|||||||
|
|
|
|
|
1 r2 |
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
tкр t1 0,05;38 t0,95;38 2,02. |
|
|
||||||||||||
4. |
|
|
На |
|
|
|
|
выбранном |
уровне |
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
Так |
как |
tнаб 7,54 2,02, |
то |
|||||||||||||||||
значимости |
|
|
и |
по |
числу |
|
|
|||||||||||||||||||||
степеней свободы k |
определить |
|
|
следует |
признать значимую |
связь |
||||||||||||||||||||||
критическое значение |
|
|
|
между |
количеством |
выпускаемой |
||||||||||||||||||||||
tкр t1 ,k (см. прил. 3) |
|
|
|
продукции и полными затратами на их |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
производство |
|
|
|
|
|
|
5. Если |
|
|
tнаб |
|
tкр , |
то гипотеза |
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
H0 |
будет отвергаться |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Корреляционная таблица |
|
|
|
|
|
||||
|
|
|
|
Данные о |
статистической |
зависимости величин |
X |
и |
Y |
для |
||||||||||||||||||
сгруппированной выборки удобно задавать в виде корреляционной |
||||
таблицы. Пусть |
|
И |
||
случайная величина X |
в |
выборке принимает |
||
значения x1,x2, ,xk , а величина Y |
– значения |
y1,y2, ,ym , где k и |
||
m – количество |
различающихся |
Д |
|
|
между |
собой значений данных |
|||
таблицу (табл. 4.8), которая определяет соответствие между парой
случайных величин. Полученные данные заносят в корреляционную |
|
|
А |
б |
|
и |
|
значений (xi, yj ) с учетом частот встречаемости.
Таблица 4.8
Корреляционная таблица
Y / X |
|
x1 |
С |
|
x2 |
… |
xk |
|
nY |
|
y1 |
|
n11 |
|
|
n21 |
… |
nk1 |
|
ny |
|
|
|
|
|
|
|
|
|
|
1 |
|
… |
|
… |
|
|
… |
… |
… |
|
… |
|
|
|
|
|
|
|
|
|
|
|
|
ym |
|
n1m |
|
|
n2m |
… |
nkm |
|
ny |
|
|
|
|
|
|
|
|
|
|
m |
|
nX |
|
nx1 |
|
|
nx2 |
… |
nxk |
|
n |
|
|
В таблице nxi , nyj |
– частоты вариант xi |
и yj |
соответственно, nij |
||||||
– частота пары (xi, yj ). Объём выборки можно получить одной из сумм n nX nY nXY .
102
Исследование линейной зависимости между случайными величинами X и Y по сгруппированной выборке проводят по схеме, приведенной в табл. 4.9.
Таблица 4.9
Исследование линейной зависимости между случайными величинами
|
|
|
Этапы исследования |
|
|
|
Код |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Задание |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
||||||||
1. Построение |
корреляцион- |
4.1 |
По |
|
данным |
корреляционной |
таблицы |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
ного поля. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
исследовать |
корреляционную |
и |
|||||||||||||||||||||||||||||||||||||||||
2. Нахождение уравнений ре- |
|
регрессионную зависимости между Х и Y. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
грессии. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
коэффициен- |
|
|
|
|
|
|
Y |
|
|
|
|
|
X |
|
|
1 |
|
|
3 |
|
5 |
|
n |
|
||||||||||||||||||||||||
3. Нахождение |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Y |
|
|||||||||||||||||||||||||||||||||||||||||
та корреляции. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
4 |
|
2 |
|
|
|
|
|
6 |
|
|
|||||||||||||||||||||||||||||||||||
4. Проверка |
|
|
значимости |
|
ко- |
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
5 |
|
1 |
|
|
|
6 |
|
|
|||||||||||||||||||||||||||||||||||||||
эффициента корреляции. |
|
|
|
|
|
|
|
|
|
|
9 |
|
|
|
|
|
|
3 |
|
5 |
|
|
|
8 |
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
nX |
|
|
|
4 |
|
10 |
6 |
|
|
|
20 |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Нахождение |
|
|
|
|
|
|
|
генеральных |
|
|
|
|
|
|
Д |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
средних |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
(1 4 3 10 5 6) 3,2 |
; |
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
20 |
|
|
|
|
|
|
|
И |
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
1 k |
|
|
|
|
|
|
|
|
|
|
|
|
|
; y |
|
1 m |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
x |
|
|
x n |
|
|
|
|
|
|
|
|
|
|
y |
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
(1 6 5 6 9 8) 5,4 |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
ni 1 |
|
i |
|
|
Xi |
|
|
n j 1 |
j |
|
Yj |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
20 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Нахождение |
|
|
|
|
|
|
|
|
групповых |
б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
средних |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
А |
|
|
|
X |
|
|
|
|
|
1 |
|
|
3 |
|
|
5 |
|
|
|
||||||||||||||||||
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
и |
|
|
|
yi |
|
|
|
|
|
1 |
|
|
5,4 |
|
8,3 |
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
yjnij |
|
|
|
|
|
|
|
|
|
|
xinij |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
y |
|
j 1 |
|
|
|
|
|
|
|
|
|
|
|
|
; |
|
|
x |
|
|
i 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
i |
|
|
|
|
|
|
|
nX |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
j |
|
|
|
nY |
|
|
|
|
|
|
|
|
|
|
|
|
|
Y |
|
|
|
|
|
1 |
|
|
5 |
|
9 |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
С |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
xj |
|
|
1,67 |
|
|
3,3 |
|
4,25 |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
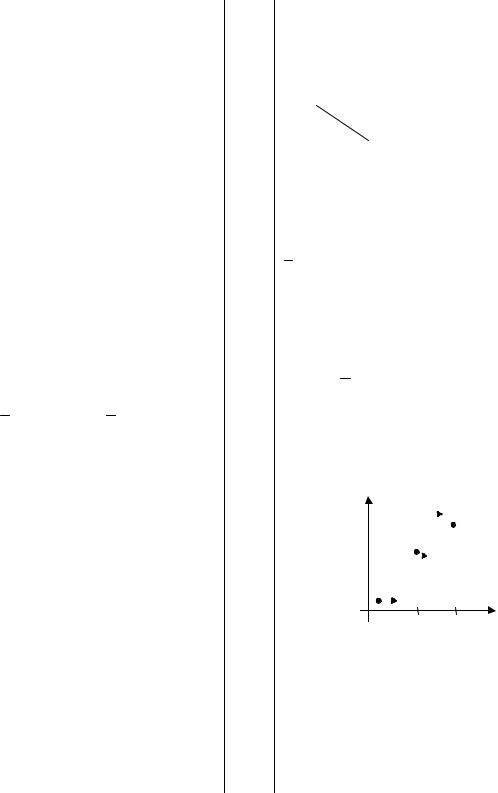
Построение поля корреляции |
4.1 |
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
Y на Х (черные точки) и Х на |
|
|
|
|
|
|
|
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
Y (черные треугольники) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
3 |
|
5 |
|
|
x |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|||||||||
Определение коэффициентов |
4.2 |
|
|
|
|
|
1 |
2 |
|
|
|
|
|
2 |
|
|
2 |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
регрессии |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
(1 |
|
4 3 10 5 6) 12,2; |
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
21 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
yx |
|
xy |
|
|
x |
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
(1 1 4 1 3 2 5 3 5 |
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
xy |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
x2 x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
20 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 5 1 9 3 3 9 5 5) 20,8; |
|
|
|
|||||||||||||||||||||||
|
xy |
|
|
xy x y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y2 40,2; yx |
1,8; |
xy |
0,32 |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
y |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
103
