
- •Введение
- •КОДИФИКАТОР РАЗДЕЛА «МАТЕМАТИЧЕСКАЯ СТАТИСТИКА»
- •ВВЕДЕНИЕ В МАТЕМАТИЧЕСКУЮ СТАТИСТИКУ
- •Предельные теоремы теории вероятностей
- •Основные законы распределения непрерывных случайных величин
- •Законы распределения случайных величин, связанные с нормальным распределением
- •Глава 1. ВЫБОРКИ И ИХ ХАРАКТЕРИСТИКИ
- •1.1. Справочный материал
- •Задачи математической статистики
- •Основные понятия математической статистики
- •Графическое изображение статистического ряда распределения
- •Эмпирическая функция распределения
- •Числовые характеристики статистического ряда
- •Моменты случайных величин
- •1.2. Задания в тестовой форме
- •Элемент 1.1. Статистическое распределение выборки
- •Элемент 1.2. Основные числовые характеристики выборки
- •Элемент 1.3. Дополнительные числовые характеристики выборки
- •1.3. Варианты заданий для расчетной работы «Первичная обработка статистических данных»
- •1.4. Образец для выполнения расчетной работы «Первичная обработка статистических данных»
- •Глава 2. ЭЛЕМЕНТЫ ТЕОРИИ ОЦЕНОК
- •2.1. Справочный материал
- •Понятие статистической оценки и ее свойства
- •Точечные оценки и их нахождение
- •Выравнивание статистического ряда
- •Интервальные оценки
- •2.2. Задания в тестовой форме
- •Элемент 2.1. Точечные оценки
- •Элемент 2.2. Интервальные оценки
- •2.4. Образец для выполнения расчетной работы «Выравнивание статистических рядов»
- •Глава 3. ПРОВЕРКА СТАТИСТИЧЕСКИХ ГИПОТЕЗ
- •3.1. Справочный материал
- •Понятие статистической гипотезы и ее виды
- •Критическая область и ее нахождение
- •Проверка параметрических гипотез
- •3.2. Задания в тестовой форме
- •Элемент 3.1. Статистические гипотезы
- •Элемент 3.2. Ошибки проверки статистических гипотез
- •Элемент 3.3. Критическая область
- •Элемент 3.4. Проверка статистических гипотез
- •3.3. Варианты заданий для расчетной работы «Проверка гипотезы о равенстве генеральных дисперсий»
- •3.5. Варианты заданий для расчетной работы «Проверка гипотезы о законе распределения генеральной совокупности по критерию Пирсона»
- •4.1. Справочный материал
- •Зависимости между случайными величинами
- •Корреляционное поле
- •Линейная парная регрессия
- •Нелинейная парная регрессия
- •Коэффициент корреляции и его свойства
- •Проверка значимости коэффициента корреляции
- •Корреляционная таблица
- •Корреляционное отношение и его свойства
- •4.2. Задания в тестовой форме
- •Элемент 4.2. Уравнение регрессии
- •Элемент 4.3. Коэффициент корреляции
- •Элемент 4.4. Корреляционное отношение
- •4.3. Варианты заданий для расчетной работы «Подбор уравнения регрессии для бесповторной выборки»
- •4.4. Образец для выполнения расчетной работы «Подбор уравнения регрессии для бесповторной выборки»
- •Библиографический список

Глава 4. ЭЛЕМЕНТЫ КОРРЕЛЯЦИОННОРЕГРЕССИОННОГО АНАЛИЗА
4.1. Справочный материал
Зависимости между случайными величинами
Корреляционный и регрессионный анализ предназначены для изучения по выборочным данным зависимости ряда величин, некоторые из которых являются случайными (табл. 4.1).
Основная задача регрессионного анализа – установление формы и изучение зависимости между переменными. Основная задача корреляционного анализа – выявление связи и оценка степени тесноты между случайными переменными.
|
|
|
|
|
Таблица 4.1 |
|
|
|
|
|
Д |
Зависимости между случайными величинами |
|||||
Вид зависимости |
|
Код |
|
|
Определение |
Функциональная |
|
4.1 |
Изменение |
величины Х влечет за собой |
|
|
|
|
А |
||
|
|
определенное изменениеИвеличины Y |
|||
Статистическая |
|
|
Изменение величины X влечет за собой изменение |
||
|
|
б |
|
||
|
|
|
распределения величины Y |
||
Корреляционная |
|
|
Изменение величины X влечет за собой изменение |
||
|
и |
|
|
||
|
|
|
среднего значения величины Y |
||
Таким образом, корреляц онная зависимость – частный случай |
|||||
С |
|
|
имеет место функциональная |
||
статистической |
зав с мости, когда |
||||
зависимость между значениями одной из них и математическим ожиданием другой.
Виды представления корреляционной зависимости:
|
f (x) M(Y / X x) |
– уравнение регрессии Y на X ; |
||||
|
g(y) M(X /Y y) |
– уравнение регрессии X на Y . |
||||
Оценками данных функций служат выборочные уравнения |
||||||
регрессии (условные средние): |
|
|||||
|
|
x f (x,b0 ,b1,...,bp ), где |
y |
x |
– условная средняя переменной Y |
|
|
y |
|||||
при фиксированном значении |
переменной X x; b0 ,b1,...,bp – |
|||||
параметры кривой регрессии. |
|
|||||
95
xy g (x,c0,c1,...,cp ), где xy – условная средняя переменной X
при фиксированном значении переменной Y y; c0,c1,...,cp – параметры кривой регрессии.
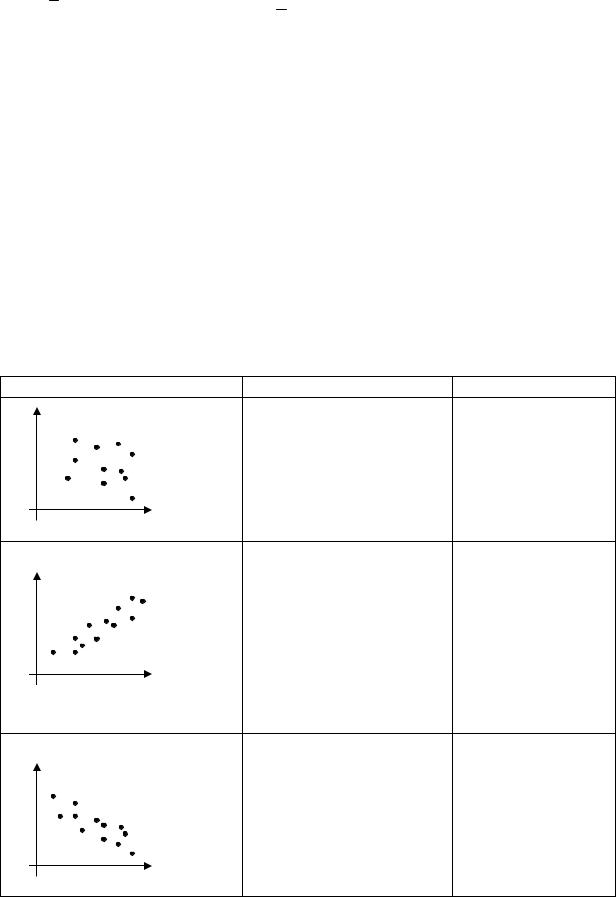
Корреляционное поле
Наиболее простым и эффективным способом выявления зависимости между изучаемыми признаками является графический метод. Для этого на координатном поле наносят точки, соответствующие значениям изучаемых признаков. Совокупность точек образует корреляционное поле. По характеру расположения
точек на корреляционном поле можно судить о направлении и силе |
||||||||||
y |
|
|
|
|
|
|
И |
|
|
|
связи (табл. 4.2). |
|
|
|
Д |
|
|
|
|||
|
|
|
|
|
|
|
|
|
Таблица 4.2 |
|
|
Анализ зависимости между признаками по виду корреляционного поля |
|||||||||
|
Корреляционное поле |
|
Анализ данных |
|
Вывод |
|||||
|
|
|
|
А |
|
|
Зависимость |
между |
||
|
|
|
Точки |
беспорядочно |
||||||
|
|
|
разбросаны по полю |
X и Y отсутствует |
||||||
|
|
|
б |
|
|
|
|
|
|
|
|
x |
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
С |
Точки |
образуют |
эллипс, |
Имеется |
прямая |
||||
|
|
|
||||||||
y |
|
|
концентрируются |
вокруг |
зависимость |
между |
||||
|
|
|
оси, идущей из нижнего |
X и Y |
|
|
||||
|
|
|
левого |
угла |
в |
верхний |
|
|
|
|
|
|
|
правый |
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
Точки |
образуют |
эллипс, |
Имеется обратная |
||||
y |
|
|
концентрируются |
вокруг |
зависимость |
между |
||||
|
|
|
оси, идущей из нижнего |
X и Y |
|
|
||||
|
|
|
левого |
угла |
в |
верхний |
|
|
|
|
|
|
|
правый |
|
|
|
|
|
|
|
96
Линейная парная регрессия
Рассмотрим простую регрессию Y на Х, выборочные данные для которой представлены в табл. 4.3.
|
|
|
|
|
|
|
|
|
|
|
|
|
Выборочные данные |
|
|
|
|
Таблица 4.3 |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
xi |
|
|
|
|
|
|
|
|
x1 |
|
x2 |
|
|
|
|
… |
|
|
|
|
xn |
|
||
|
|
yi |
|
|
|
|
|
|
|
|
y1 |
|
y2 |
|
|
|
|
… |
|
|
|
|
yn |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
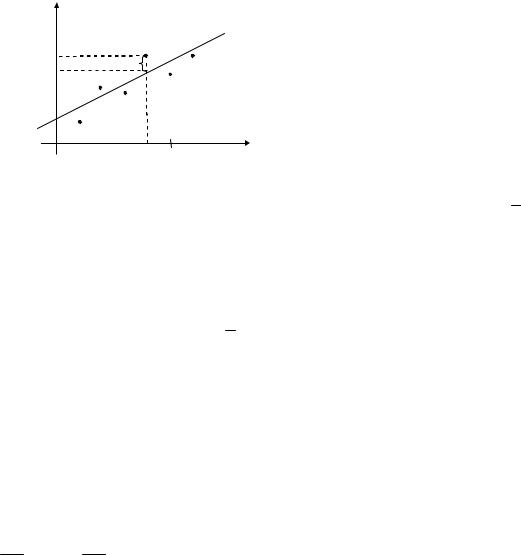
Построим корреляционное поле |
||||||||||
|
|
Y |
|
|
|
|
|
|
|
|
|
|
|
|
по выборочным данным (рис. 4.1). |
|
||||||||||
|
|
|
|
|
|
|
|
|
x |
аx b |
|
Линейная |
|
парная |
регрессия |
|||||||||||
|
|
|
|
|
|
|
|
y |
|
|
||||||||||||||||
|
|
yi |
|
|
|
i |
|
|
|
|
сводится |
к |
нахождению |
регрес- |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
сионного уравнения вида yx |
ax b. |
|||||||||||||||
yx (xi ) |
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Уравнение |
|
позволяет |
по |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
X |
заданным |
значениям хi |
вычислить |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
теоретические |
|
значения |
|
результа- |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
x1 x2 xi |
xn |
|
|
||||||||||||||||||||
|
|
|
тивного признака Y. На графике |
|||||||||||||||||||||||
|
|
Рис. 4.1. Корреляционное поле |
|
|
|
И |
|
|
|
|
предста- |
|||||||||||||||
|
|
теоретические |
|
значения |
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
вляют прямую регрессии |
y |
x |
ax b. |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Д |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
А |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
б |
|
|
|
|
|
|
|
|
|
|
|
||
Для оценки параметров а и b регрессии при классическом подходе используется метод наименьших квадратов.
Метод наименьш х квадратов позволяет получить такие оценки
С |
|
|
|
|
|
|
|
|
параметров, при которых сумма квадратов отклонений эмпирических |
||||||||
значений yi от значен й |
y |
x |
(x ), найденных по уравнению регрессии, |
|||||
|
|
|
|
i |
|
|
|
|
была минимальной, ти.е. |
|
|
|
|||||
|
|
k |
|
k |
|
|
|
|
|
S i2 (yi |
|
|
x )2 min. |
||||
|
y |
|||||||
|
|
i 1 |
i 1 |
|
|
|
||
|
|
|
|
|
|
|
|
n |
Для линейной зависимости имеем S axi b yi 2 . |
||||||||
Функция S |
|
|
|
|
|
|
|
i 1 |
имеет минимум в тех точках, в которых частные |
||||||||
производные от |
S по параметрам a |
и b обращаются в нуль, т.е. |
||||||
S 0 и S 0. В результате дифференцирования и преобразований
a b
получаем систему линейных уравнений для определения a и b:
97

|
n |
n |
n |
a x2 |
b x x y ; |
||
|
i |
i |
i i |
|
i 1 |
i 1 |
i 1 |
|
n |
|
n |
|
a x b n y . |
||
|
i 1 |
i |
i |
|
|
i 1 |
|
Разделив обе части уравнений на n, получим систему нормальных
|
b ax |
|
y |
; |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
1 n |
|
|
1 n |
|||||
|
|
|
|
|
|
|
|
|
|
||||||||
уравнений |
|
|
|
|
|
|
|
где |
x |
|
xi ; |
y |
|
yi ; |
|||
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
||||||||||
bx |
ax2 |
xy, |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
ni 1 |
|
|
ni 1 |
|||||
___
x2 1 n x2 . Выразим из первого уравнения системы ni 1 i
___xy 1 n xi yi ; ni 1
b y ax и
подставим |
|
в |
|
|
|
уравнение регрессии |
|
|
y |
x ax b ax |
y |
ax |
или |
|||||||||||||||||||||||||||||||||||||||||||
|
y |
x |
y |
|
a(x |
x |
). |
Коэффициент |
a |
|
|
называют |
коэффициентом |
|||||||||||||||||||||||||||||||||||||||||||
регрессии Y по Х и обозначают символом |
|
|
И |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
yx (табл. 4.4). |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Коэффициент линейной регрессии |
|
|
|
|
|
Таблица 4.4 |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Понятия |
|
|
|
А |
|
|
|
|
|
Задание |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Код |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
В уравнении |
|
регрессии |
Y по Х |
4.2 |
Получены |
результаты |
|
|
|
измерений |
||||||||||||||||||||||||||||||||||||||||||||||
|
y |
x |
y |
|
yx(x |
x |
), |
|
|
|
|
|
значений величин Х и Y: |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
б |
Дxi 4 |
|
6 |
|
|
8 |
|
10 |
|
12 |
|
|
|||||||||||
|
|
|
|
|
|
|
|
xy |
x y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
yx |
|
|
|
– |
коэффициент |
|
yi |
|
|
5 |
|
8 |
|
|
7 |
|
9 |
|
14 |
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Найти линейную регрессию Y на Х, |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
x2 x2 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
регрессии Y |
|
|
|
|
|
по |
X , который |
|
yx |
и xy. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
показывает, на сколько в среднем |
|
Решение. |
Составляем |
|
|
|
расчетную |
|||||||||||||||||||||||||||||||||||||||||||||||||
изменяется переменная |
Y |
при |
|
таблицу: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
увеличении |
переменной |
|
Х |
на |
|
i |
|
|
|
|
xi |
yi |
|
2 |
|
|
|
xi yi |
2 |
|
|
|||||||||||||||||||||||||||||||||||
единицу |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xi |
|
|
|
yi |
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
4 |
|
5 |
|
|
16 |
|
20 |
|
25 |
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
6 |
|
8 |
|
|
36 |
|
48 |
|
64 |
|
|
|||||||
В уравнении регрессии Х |
|
по Y |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
С |
|
|
|
3 |
|
|
8 |
|
7 |
|
|
64 |
|
56 |
|
49 |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
xy x xy (y |
y), |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
4 |
|
|
10 |
|
9 |
|
|
100 |
|
90 |
|
81 |
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
xy |
|
x |
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
xy |
|
|
|
– |
коэффициент |
|
5 |
|
|
12 |
|
14 |
|
|
144 |
|
168 |
196 |
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
y2 |
y |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
40 |
|
43 |
|
|
360 |
|
382 |
405 |
|
||||||||||||||||||
регрессии X по Y показывает, |
|
Система |
нормальных |
|
|
|
|
уравнений |
|
|||||||||||||||||||||||||||||||||||||||||||||||
на сколько в среднем изменяется |
|
40b 360a 382; |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
переменная |
Х |
при |
увеличении |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
5b 40a 43, |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
переменной Y на единицу |
|
|
|
|
откуда |
y |
x 0,95x 1; а yx 0,95; |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xy |
|
382/5 40/5 43/4 |
1,88 |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
405/5 (43/5)2 |
|
|
|
|
|
|
|
|
|
|||||||
98
