3.5. Варианты заданий для расчетной работы «Проверка гипотезы о законе распределения генеральной совокупности по критерию Пирсона»

Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Сибирская государственная автомобильно-дорожная академия

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

1834.pdf

Скачиваний:

Добавлен:

07.01.2021

Размер:

1.93 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 13 1415 / 2115 16 17 18 19 20 21 > Следующая >>>

Близость к

нулю полученного значения коэффициента

Для разумного планирования и организации работы ремонтных мастерских специальной техники оказалось необходимым изучить длительность ремонтных операций, производимых мастерскими. Получены результаты (сгруппированные по интервалам) соответствующего статистического обследования (фиксированы длительности операций в 100 случаях):

x ,x

x1;x2

…

i i

…

Требуется:

1) построить гистограмму частостей;

2) найти числовые характеристики выборки (

, S , A,

E);

3) по виду гистограммы и значениямИчисловых характеристик

выдвинуть гипотезу о законе распределения случайной величины X –

длительности

оценить

параметры

ремонтных

операций,

теоретического закона и записать его вид;

4) проверить основную гипотезу о законе распределения Х по

критерию Пирсона (уровень значимости выбрать самостоятельно);

гипотезы

законе

5) проверить две альтернативных

распределения Х по кр тер ю Пирсона.

иВариант 1

xi,xi 1

[0;3)

[3;6)

[6;9)

[9;12)

[12;15)

[15;18)

[18;21)

[21;24)

Вариант 2

xi,xi 1

[0;3)

[3;6)

[6;9)

[9;12)

[12;15)

[15;18)

[18;21)

[21;24)

Вариант 3

xi,xi 1

[0;3)

[3;6)

[6;9)

[9;12)

[12;15)

[15;18)

[18;21)

[21;24)

Вариант 4

xi,xi 1

[0;3)

[3;6)

[6;9)

[9;12)

[12;15)

[15;18)

[18;21)

[21;24)

Вариант 5

xi,xi 1

[0;3)

[3;6)

[6;9)

[9;12)

[12;15)

[15;18)

[18;21)

[21;24)

Вариант 6

xi,xi 1

[0;3)

[3;6)

[6;9)

[9;12)

[12;15)

[15;18)

[18;21)

[21;24)

Вариант 7

xi,xi 1

[0;3)

[3;6)

[6;9)

[9;12)

[12;15)

[15;18)

[18;21)

[21;24)

Вариант 8

x ,x

[0;3)

[3;6)

[6;9)

[15;18)

[18;21)

[21;24)

[9;12)

[12;15)

i i 1

Вариант 9

xi,xi 1

[0;3)

[3;6)

[9;12)

[12;15)

[15;18)

[18;21)

[21;24)

[6;9)

бВариант 10

xi,xi 1

[0;3)

[3;6)

[6;9)

[9;12)

[12;15)

[15;18)

[18;21)

[21;24)

Вариант 11

xi,xi 1

[0;3)

[3;6)

[6;9)

[9;12)

[12;15)

[15;18)

[18;21)

[21;24)

Вариант 12

xi,xi 1

[0;3)

[3;6)

[6;9)

[9;12)

[12;15)

[15;18)

[18;21)

[21;24)

Вариант 13

xi,xi 1

[0;3)

[3;6)

[6;9)

[9;12)

[12;15)

[15;18)

[18;21)

[21;24)

Вариант 14

xi,xi 1

[0;3)

[3;6)

[6;9)

[9;12)

[12;15)

[15;18)

[18;21)

[21;24)

Вариант 15

xi,xi 1

[0;3)

[3;6)

[6;9)

[9;12)

[12;15)

[15;18)

[18;21)

[21;24)

Вариант 16

xi,xi 1

[0;3)

[3;6)

[6;9)

[9;12)

[12;15)

[15;18)

[18;21)

[21;24)

Вариант 17

x ,x

[0;3)

[3;6)

[6;9)

[15;18)

[18;21)

[21;24)

[9;12)

[12;15)

i i 1

Вариант 18

xi,xi 1

[0;3)

[3;6)

[9;12)

[12;15)

[15;18)

[18;21)

[21;24)

[6;9)

бВариант 19

xi,xi 1

[0;3)

[3;6)

[6;9)

[9;12)

[12;15)

[15;18)

[18;21)

[21;24)

Вариант 20

xi,xi 1

[0;3)

[3;6)

[6;9)

[9;12)

[12;15)

[15;18)

[18;21)

[21;24)

Вариант 21

xi,xi 1

[0;3)

[3;6)

[6;9)

[9;12)

[12;15)

[15;18)

[18;21)

[21;24)

Вариант 22

xi,xi 1

[0;3)

[3;6)

[6;9)

[9;12)

[12;15)

[15;18)

[18;21)

[21;24)

Вариант 23

	xi,xi 1	[0;3)	[3;6)	[6;9)		[9;12)	[12;15)		[15;18)	[18;21)	[21;24)
	ni	36	17	13		10		9	8	5	2
					Вариант 24

	xi,xi 1	[0;3)	[3;6)	[6;9)		[9;12)	[12;15)		[15;18)	[18;21)	[21;24)
	ni	34	16	12		11		9	8	6	4
					Вариант 25

	xi,xi 1	[0;3)	[3;6)	[6;9)		[9;12)	[12;15)		[15;18)	[18;21)	[21;24)
	ni	37	17	12		11		9	6	5	3
		3.6. Образец для выполнения расчетной работы
	«Проверка гипотезы о законе распределения генеральной
			совокупности по критерию Пирсона»
	Получены						Д
	Получены		результаты (сгруппированные по интервалам)
						А
статистического обследования длительностиИ100 ремонтных
операций, производимых мастерскими:

	xi,xi 1	[0;3)	[3;6)	[6;9)		[9;12)	[12;15)		[15;18)	[18;21)	[21;24)
	ni	43	21	и		12		3	4	2	1
	ni	43	21	14		12		3	4	2	1
	Требуется:
	1) построить г стограммубчастостей;

2)	найти числовые характеристики выборки (				х	В , S , A, E);
3)	по виду гистограммы и значениям числовых характеристик
выдвинуть гипотезу о законе распределения случайной величины X –
длительности		Сремонтных	операций,	оценить			параметры
теоретического закона и записать его вид;
4) проверить выдвинутую гипотезу о законе распределения Х по
критерию Пирсона (уровень значимости выбрать самостоятельно);
5)	проверить две альтернативных гипотезы о законе
распределения Х по критерию Пирсона.
Решение.
1)	Для	построения гистограммы		строим вспомогательную

табл. 3.6.

																								Таблица 3.6
		Расчетная таблица для построения гистограммы частостей
			Разряды											ni			*			*		i		– середина
	i		xi,xi 1					ni				i		ni		f	*	(x) h		*		i	xi	– середина
	i		xi,xi 1					ni				i			n	f		(x) h					интервала
1			[0;3)					43				0,43						0,143						1,5
2			[3;6)					21				0,21						0,07						4,5
3			[6;9)					14				0,14						0,046						7,5
4			[9;12)					12				0,12						0,04						10,5
5			[12;15)					3				0,03						0,01						13,5
6			[15;18)					4				0,04						0,013						16,5
7			[18;21)					2				0,02						0,007						19,5
8			[21;24)					1				0,01						0,003						22,5

Контроль				–		8			=100			8			=1				–						–
Контроль				–		ni			=100			i			=1				–						–
						i 1						i 1				И
						i 1						i 1

	По данным табл. 3.6 строим гистограмму частостей (рис. 3.2).
0,2											А
0,2								б					Д
0,15								б					Д
0,15					и
0,1					и
0,1
0,05

				С
0				С
0			3				6			9		12			15			18			21			24
															15						21			24

					Рис. 3.2. Гистограмма частостей
	2) Находим числовые характеристики выборки:
	k		1,5 0,43 4,5 0,21 ... 22,5 0,01 5,58;
	k
xB xi i

i1 k

DB (xi)2 i (xB)2 1,52 0,43 4,52 0,21 ... 22,52 0,01 5,582 24,22;

	i 1				100
B				4,92; S2		24,22 24,46;	S 5;
		DB	24,22

					100 1

3 (1,5 5,58)3 0,43 ... (22,5 5,58)3 0,01 1,127;

A 3 1,127 0,009; S3 125

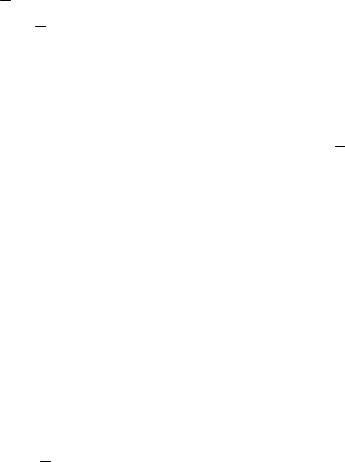
4 (1,5 5,58)4 0,43 ... (22,5 5,58)4 0,01 2448,99;

асимметрии говорит в пользу нормального закона распределения генеральной совокупности. Однако, учитывая вид гистограммы и близость статистического среднего xB и выборочного среднего квадратического отклонения B по своим значениям, выдвигаем основную гипотезу в пользу показательного закона распределения,

функция плотности которого имеет вид

0,x 0;

f (x)

,x 0.

Найдем

оценку

параметра

показательного

закона

распределения.

Выборочное

среднее

5,58

–

xB xi i

i 1

несмещенная

состоятельная

оценка

математического

ожидания.

М(Х)

Используя

метод

B .

Тогда

моментов,

имеем

0,18.

5,58

Заменяя

оценкой

получаем теоретический

закон

0,x 0;

бx

f (x)

распределения f (x)

т.е.

0,18x

,x 0.

0,18e

В качествеимеры расхождения

между

статистическим

гипотетическим (теоретическим) распределениями возьмем критерий

Пирсона 2.
	Мера		расхождения		в	этом критерии определяется равенством
2	k	(n np )2
		i	i	, где	n	– объем выборки (у нас n=100); ni –
			npi
	i 1

эмпирические частоты (число элементов в i-м интервале); k – число интервалов (у нас k=8); pi – теоретические вероятности попадания значений случайной величины в i-й интервал; npi – теоретические частоты.

В рассматриваемом эмпирическом распределении (см. табл. 3.6) имеются частоты, меньшие 5. При использовании критерия Пирсона

такие интервалы целесообразно объединять с соседними. После объединения интервалов с низкой степенью частоты получим интервальный ряд:

xi,xi 1

[0;3)

[3;6)

[6;9)

[9;12)

[12;24)

100

Находим теоретические вероятности Pi

по формуле

f (x)dx

dx е

| i

i 1

i ,

xi 1

i 1

где

0,18.

Для нахождения вероятностей воспользуемся прил. 6.

0,18e 0,18xdx e 0,18x

(e 0,18 3 e0) 1 e 1 1 0,5827 0,42;

e 0,18x

e 1,08

e 0,54 0,365 0,583 0,22;

e 0,18x

e 1,62

e 1,08

0,198 0,365 0,17;

e 0,18x

e 2,16

e 1,62

0,198 0,115 0,08;

e 0,18x

e 4,32

e 2,16

0,018 0,115 0,097.

Дальнейшие выч слен я, необходимые

для

определения

расчетного

значения

выборочной

статистики

проведем

в табл. 3.7.

Таблица 3.7

Расчетная таблица для проверки гипотезы о показательном законе

распределения генеральной совокупности

xi,xi 1

[0;3)

[3;6)

[6;9)

[9;12)

[12;24)

100

npi

9,7

98,7

(ni npi )2

0,09

–

n np 2

набл2

0,02

0,05

0,53

0,33

0,009

0,939

npi

Распределение 2 зависит от числа степеней свободы r k l 1 (k – число интервалов после объединения) и уровня значимости α.

В нашем примере k=5; l=1 (так как функция плотности распределения зависит только от одного параметра ); r = 5-1-1=3.

Зададим уровень значимости α=0,05 и найдем по таблице значений 2 (см. прил. 4) критическое значение для α=0,05 и r=1. Имеем 0,05;32 7,8. Так как набл2 0,05;32 , то предполагаемая гипотеза о показательном законе распределения генеральной совокупности не противоречит опытным данным и принимается на уровне значимости

α=0,05.

Проверим

альтернативную

гипотезу

о распределении

генеральной

совокупности

по

функция

нормальному

закону,

(x a)2

плотности которого имеет вид f (x)

2 .

Оценим

по

выборке

параметры

нормального

закона

распределения а и . По методу моментов в качестве оценок а и

примем

соответственно

выборочную

среднюю

В 5,58 и

исправленное выборочное среднее квадратическое отклонение S 5.

Заменяя

а и найденными оценками, получаем вид теоретического

(x 5,58)2

закона распределен

я: f (x)

2 62

2 5

Находим теорет ческ е вероятности pi по формуле

Ф(х)

pi P xi

X xi 1 Ф

i 1

где

–

функция

Лапласа (см. прилС. 2).

p ( X 3) Ф

3 5,58

5,58

0,5-0,1985=0,30;

6 5,58

3 5,58

0,0319+0,1985=0,23;

p2 (3 X 6) Ф

p (6 X 9) Ф

9 5,58

6 5,58

0,2517-0,0319=0,22;

12 5,58

9 5,58

0,3997-0,2517=0,15;

p2 (9 X 12) Ф

p	(12 X ) Ф	5,58	Ф	12 5,58		0,5-0,3997=0,10.

3		5			5

Все вычисления, необходимые для определения расчетного значения выборочной статистики 2 , проведем в табл. 3.8.

Таблица 3.8

Расчетная таблица для проверки гипотезы о нормальном законе распределения генеральной совокупности

	xi,xi 1		[0;3)	[3;6)		[6;9)		[9;12)	[12;24)

		ni	43	21			14	12	10		100
		npi	30	23			22	15	10		100
	(ni	npi )2	169	4			64	9		0		–
	n np 2							И
	i	i	5,6	0,17			2,9	0,6		0	набл2	9,27
		npi	5,6	0,17			2,9	0,6		0	набл2	9,27
		npi
		Зададим уровень значимости α = 0,05 и найдем по таблице
значений 2			(см. прил. 4)		критическое значение для						α = 0,05 и

r = 5-2-1=2 (k = 5; l = 2, так как функция плотности распределения

зависит двух от параметров). Имеем

6,0.

Так

как 2

2 ,

Д0,05;2

набл

кр

то альтернативная

гипотеза

нормальном законе распределения

генеральной

противоречитА

опытным данным и

совокупности

отвергается на уровне знач мости α= 0,05.

Проверим альтернатбвную гипотезу о распределении

генеральной

совокупности

по

равномерному

закону,

функция

x a;b ;

плотности которого имеет вид

f (x) b a

x a;b .

Оценим по выборке параметры

равномерного закона

3 B;

распределения по

методу моментов,

имеем

a xB

Тогда

b xB

3 B.

3 5 3,08;

a 5,58

Заменяя а

найденными

оценками,

b 5,58

3 5 14,24.

получаем

вид

теоретического

закона

распределения

f (x) 0,057;

x 3,08;14,24 . Находим теоретические вероятности

pi по формуле p

f (x)dx

x ,x

3,08;14,24 .

0,057dx, где

xi 1

i i 1

p1 0,057dx 0,057 3 0,171;

p2 0,057dx 0,057 3 0,171;

p3 0,057dx 0,057 3 0,171;

0,057dx 0,057 3 0,171;

14,24

0,057dx 0,057 2,24 0,128.

Далее вычисления, необходимые для определения расчетного

значения выборочной статистики 2 , проведем в табл. 3.9.

Таблица 3.9

Расчетная таблица для проверки гипотезы о равномерном законе

распределения генеральной совокупности

xi,xi 1

[0;3)

[3;6)

[6;9)

[12;24)

[9;12)

100

npi

17,1

12,8

81,2

(n np )2

671

15,21

9,61

26,01

7,84

–

npi 2

39,24

0,56

1,52

набл2

42,67

npi

Пусть уровень знач мости α=0,05, найдем критическое значение

для α = 0,05 и r =5-2-1=2 (k = 5; l = 2, так как функция плотности

распределения зависит от двух параметров). Имеем 0,05;2

6,0. Так

как

2 , то

альтернативная гипотеза о

равномерном

законе

набл

кр

распределения генеральной совокупности противоречит опытным данным и отвергается на уровне значимости α=0,05.

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 13 1415 / 2115 16 17 18 19 20 21 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
07.01.2021333.26 Кб3183.pdf
#
07.01.20211.92 Mб11830.pdf
#
07.01.20211.93 Mб21831.pdf
#
07.01.20211.93 Mб221832.pdf
#
07.01.20211.93 Mб51833.pdf
#
07.01.20211.93 Mб951834.pdf
#
07.01.20211.94 Mб21835.pdf
#
07.01.20211.94 Mб21836.pdf
#
07.01.20211.94 Mб41837.pdf
#
07.01.20211.95 Mб251838.pdf
#
07.01.20211.95 Mб01839.pdf