Глава 3. ПРОВЕРКА СТАТИСТИЧЕСКИХ ГИПОТЕЗ

Виды статистических гипотез

Таблица 3.1

Понятия

Код

Задание

H0 – нулевая (основная)

3.1

И

H0 :MX 4.

выдвигаемая гипотеза.

Составить конкурирующую гипотезу.

H1 – конкурирующая (аль-

Решение. Конкурирующая гипотеза может

тернативная)

гипотеза,

иметь

вид

H1 :MX 4;

H1 :MX 4;

которая противоположна H0

H1 :MX 4

Простой называют гипотезу,

3.1

АX

Какая из представленных гипотез является

состоящую

из

одного

простой:

H : X

5;

H : X

5;

значения

параметра.

В

H : Д5?

противном

случае

гипотеза

X

Решение.

Простой

является

гипотеза

сложная

H :

5,

т.к. она содержит только одно

предположение

С

–

б3.1 Укажите, какие из представленных гипотез

Параметрическая гипотеза

гипотеза

о

параметре

являются непараметрическими:

неизвестного распределенияи.

H :a 0, 2

1;

H : X ~ N(a, ) ;

Непараметрическая

H : X ~ R a,b ;

H :MX 5.

гипотеза –

гипотеза о виде

Решение.

Непараметрические

гипотезы:

неизвестного распределения

гипотеза о предположении, что случайная

величина

Х

подчиняется

нормальному

закону распределения или равномерному

закону,

т.е.

H : X ~ R a,b

и

H : X ~ N(a, )

характеристику K(x1,x2, ,xn )

Д

– статистику критерия, которая

А

Стьюдента, F -распределение Фишера–СнедекораИи др.). Множество

возможных значений статистики критерия K разбивается на два

б

непересекающихся подмножества: область допустимых значений

критерия и критическую о ласть.

и

С

0

области находится по стат ст ке критерия. Вид критической области

зависит от выбора альтернат вной гипотезы (табл. 3.2).

Виды критических областей

Таблица 3.2

Критическая область

Код

H :MX C

1

2

3

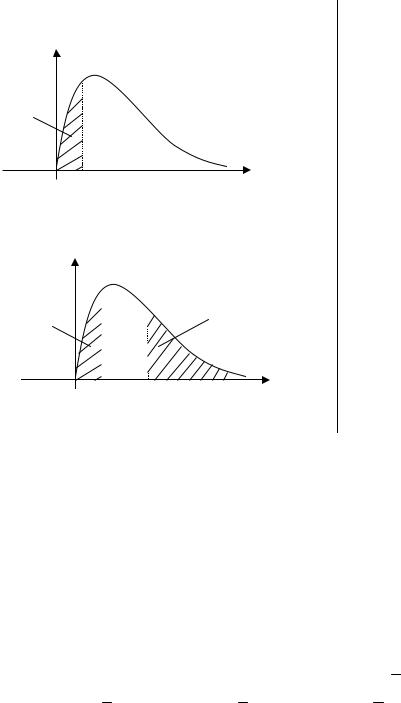
Правосторонняя: P(K Kкр)

3.3

f (K)

H1 :MX C

Kкрп ,

K

Окончание табл. 3.2

1

2

3

Левосторонняя: P(K Kкр)

3.3

f (K)

H1 :MX C

Kкрл ,

K

л

п

3.3

Двусторонняя: P(K Kкр) P(K

Kкр)

2

f (K)

H1 :MX C

2

Д

2

А

И

Kкрл ,

Kкрп ,

K

б

Проверка параметрических гипотез

С

значениях

параметров

встречаются в

Гипотезы о ч словых

различных задачах. Напр мер, случайная величина Х – средний

диаметр подшипникови, a –

заданный номинальный

диаметр

подшипника. Каждое значение

xi случайной величины

Х может

очевидно,

нужно

проверить гипотезу

H0:

x

a

против

альтернативной H1:

x

a, или H1:

x

a, или

H1:

x

a.

Процедура

Этапы

Код

Задание

1. На основании результатов

3.4

Для

проверки эффективности новой

выборки

x1,x2, ,xn

технологии отобраны две группы рабочих

случайной

величины

X

численностями: в первой группе

n1 50

формируют нулевую

H0

и

чел., где применялась новая технология и

альтернативную H1 гипотезы

x

85

изделий, во второй группе

n 70

2

2. Выбирают статистический

3.4

чел., где применялась

старая

технология

критерий К

изделий.

Предварительно

y 78

3. Задают

уровень

значи-

3.4

установлено х2

100;

y2 74.

мости α и по множеству

возможных значений стати-

На

уровне

значимости

0,05

выяснить

стики критерия определяют

влияние новой технологии на среднюю

критическую область.

производительность.

Находят критическую точку

Решение. 1. Выбираем основную

гипотезу

Kкр по

таблицам

значений

H0

:

x

0

y

0

, т.е. средние

выработки

статистического критерия

Д

рабочих одинаковы

по

новой

и

старой

4. По результатам выборки

3.4

технологиям.

Выбираем

H

:

x

y

,

что

x1,x2, ,xn

рассчитывают

И

1

0

0

наблюдаемое

значение

означает эффективность применения новой

технологии.

статистического

критерия

2. При проверке равенства средних двух

Кнаб

совокупностей используем статистику

А t

5. Сравнивают наблюдаемое

3.4

x y

.

значение критерия с Кнаб :

2

а)

Kнаб Kкр

H0

б

x2

y

С

n1

n2

отвергается (правосторонняя

3. Критическое

значение

статистики

критическая область);

и

находится

из

условия

Ф(t

) 1 2 .

б)

Kнаб Kкр

H0

кр

отвергается

(левосторонняя

Тогда имеем

Ф(tкр) 1 2 0,05 0,9.

Из

критическая область);

прил. 2 определяем tкр 1,64.

в)

Kнаб Kкрп

и

4. Находим

фактическое

значение

Kнаб Kкрл

H0 отвер-

статистики критерия t

85 78

4.

100

74

гается (двусторонняя кри-

тическая область)

50

70

5. Так как

tнаб tкр(4 1,64),

то гипотеза

H0 отвергается, т.е. на 5 %-ном уровне

значимости можно сделать вывод, что

новая

технология

позволяет

повысить

среднюю выработку рабочих

Таблица 3.4

Критерии проверки параметрических гипотез о числовых значениях

параметров нормального закона распределения

H0

H1

Предпо-

Статистика

Критерий отклонения

ложения

критерия

гипотезы H0

2

uнаб

x a0

uнаб

uкр ,

где

uкр

–

корень

известна

/

n

уравнения Ф(uкр) 1

2

a a0

a a0

tнаб

t

,

где

t

,n 1

–

,n 1

2

2

x a0

2

tнаб

%-ная

точка

распре-

неизвестна

S /

n

100

2

деления Стьюдента

с

(n 1)

степенями свободы

2

2

и

2

2

,

наб

наб

,n 1

1

2

,n 1

2

12

nS2

2

2 02

a

2

где

2

;

2

–

02

12

неизвестно

наб

02

2,n 1

1 2,n 1

И

критические значения критерия

2

Д

Замечание. Если для параметров нормального закона были

построены доверительные интервалыАи параметр не попадает в него с

надежностью

1 , т.е. попадает в критическую область, то

б

гипотеза H0 отвергается.

и

Выдвижение и проверка гипотезы о законе распределения

генеральной совокупности

С

На практике чаще всего закон распределения случайной

величины неизвестен, но результаты предварительной обработки

статистических данных (вид гистограммы относительных частот,

соотношения между выборочными характеристиками) позволяют

предположить, что распределение может подчиняться определенной

модели известного закона распределения. При выборе гипотезы в

пользу

нормального,

равномерного

или

показательного

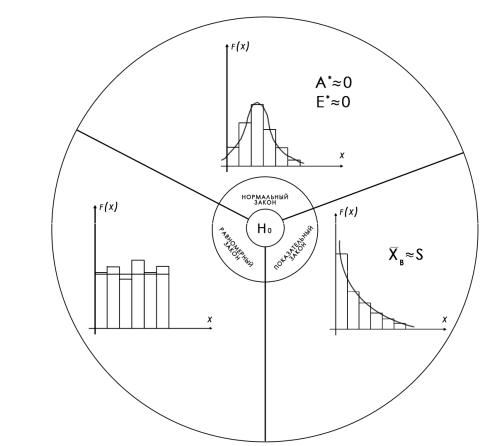
распределения можно руководствоваться схемой выдвижения

гипотезы, представленной на рис. 3.1.

И

Д

Рис. 3.1. Схема выдвижения гипотезы о законе распределения

генеральной совокупности

А

Критерии, с помощью которых проверяется непараметрическая

гипотеза о неизвестном законебраспределения, называют критериями

согласия. В табл. 3.5 рассмотрена схема применения критерия

согласия Пирсона.

и

Таблица 3.5

Проверка гипотезыСо законе распределения генеральной совокупности

по критерию Пирсона

Этапы

Код

Задание

1

2

3

1. Определить меру расхождения между

3.4

По

результатам измерений

теоретическим и выборочным распре-

200

валиков, изготовленных

делениями по формуле

на станке-автомате, прове-

наб2

k

(n np )2

рялась гипотеза о нормальном

i

i

,

распределении размера диа-

npi

i 1

метра валика.

1

2

3

где ni

–

эмпирические частоты (ni

5,

Гипотеза

проверялась

на

иначе интервалы укрупняют); pi −

уровне значимости 0,1

по

критерию

Пирсона.

По

теоретическая

вероятность

попадания

возможных

значений

случайной

выборочным

данным

было

величины

в

интервал

xi,xi 1 ;

npi

–

сгруппировано 7 интервалов и

вычислена мера расхождения

теоретические частоты.

наб2

6,755. Укажите крит2

и

Для

вычисления

вероятностей

pi

P xi

X xi 1 используют следу-

сделайте

вывод

относительно

ющие формулы:

выдвигаемой гипотезы.

Решение.

Определим

число

xi 1

а) pi

f (x)dx;

степеней свободы: k 7; l 2

xi

(для нормального распре-

б) в случае гипотезы о нормальном

деления

оцениваются

два

распределении

параметра - МХ и ), значит,

p Ф

xi 1

x

B

Ф

xi

x

B

;

r 7 2 1 4.

По уровню значимости 0,1

i

S

S

и числу

степеней

свободы

в)

приближенная

формула

находимИ2

2

7,78.

pi

f

,

где

xi 1

xi

;

i

крит

0,1;4

xi

i

~

xi xi 1

б

ля критерия

2 имеет

место

xi

Дправосторонняя

критическая

2

2. Определить число степеней сво оды

3.4

область (7,78; ).

r k l 1, где k

− число интерваловА;

Величина

наб2

6,755 7,78,

l − число параметров распределен

я

т.е. не попадает в критическую

С

α.

По

3.4

область. Гипотеза о том, что

3. Выбрать уровень знач мости

таблице распределен я

2

(см. пр л. 4)

размер

диаметра

валика

по выбранному уровнюизначимости α и

подчинен нормальному закону

числу

степеней

свободы

r

найти

распределения, с вероятностью

критическую точку 2

p 1 0,1 0,9

подтверждается

,r

4.

Сделать

вывод:

если

2

2

,

то

наб

,r

гипотеза

отвергается; если

2

2

,

наб

,r

то с вероятностью

p 1 гипотеза H0

принимается