2.4.Образец для выполнения расчетной работы «Выравнивание статистических рядов»

x 1

С

x 2 x 3 ... x n . Получ м вариационный ряд:

32,68; 43,43; 48,31; 50,81; 53,00; 55,00; 58,05; 61,38; 63,96; 69,26;

35,26; 44,89; 48,56; 51,32; 53,07; 55,80; 58,07; 61,38; 64,91; 69,86;

35,84; 45,04; 48,70; 51,38; 53,24; 55,81; 58,84; 62,40; 64,96; 70,45;

38,82; 45,23; 48,88; 51,41; 53,44; 55,99; 58,97; 62,45; 65,04; 71,06;

38,88; 45,53; 48,89; 51,99; 53,52; 56,16; 60,40; 62,55; 65,08; 72,72;

40,48; 46,24; 49,27; 52,12; 53,61; 56,28; 60,60; 62,72; 65,11; 72,77;

42,54; 46,24; 49,79; 52,21; 53,61; 56,72; 61,00; 63,18; 66,28; 73,46;

42,93; 46,38; 49,90; 52,70; 54,04; 57,23; 61,02; 63,58; 66,70; 75,85;

43,26; 46,72; 50,22; 52,72; 54,84; 57,75; 61,13; 63,71; 68,22; 75,92;

43,37; 48,26; 50,59; 52,72; 54,90; 58,00; 61,17; 63,82; 68,50; 76,33.

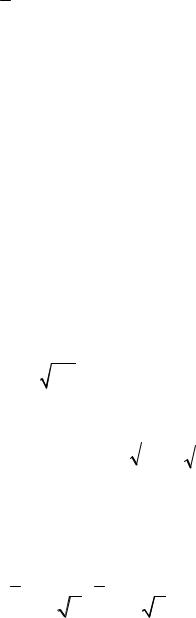
формуле Стерджеса:

R

R

, где n – объем выборки; m –

1 3,322lgn

m

число частичных интервалов. Т.к.

n 100, то

m 1 3,322lg100 9;

i-й разряд,

– середину интервала

x

;x

,

h*

i

– плотность

xi

i

i 1

i

xi ;xi 1

[32;37)

[37;42)

[42;47)

[47;52)

[52;57)

И

[67;72)

[72;77]

[57;62)

[62,67)

34,5

39,5

44,5

49,5

54,5

59,5

64,5

69,5

74,5

xi

ni

3

3

13

16

22

15

16

6

6

ni

Д

i

n

0,03

0,03

0,13

0,16

0,22

0,15

0,16

0,06

0,06

hi*

0,006

0,006

0,026

А

0,012

0,012

0,032 0,044 0,030 0,032

б

ступенчатую

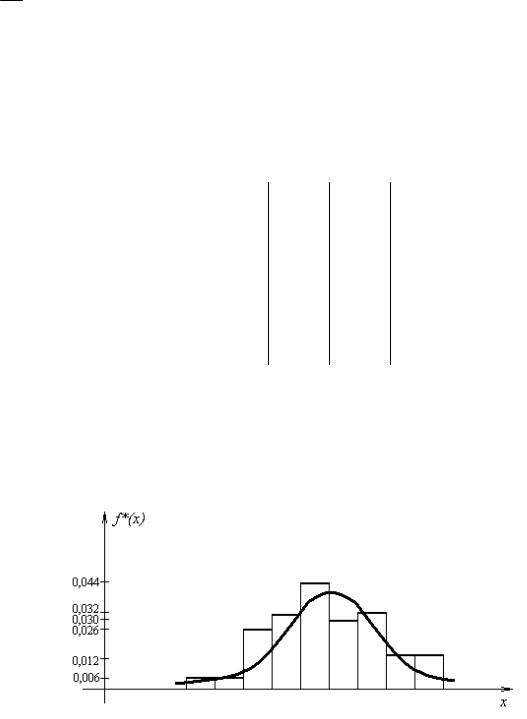
Построим гистограмму

относительных частот –

и

фигуру, состоящую из прямоугольников, основаниями которых

служат частичные

нтервалы длиной , а высоты равны hi*(рис. 2.1).

С

1

k

1

x

В

ni xi

(3 34,5 3 39,5 13 44,5 16 49,5 22 54,5

n

100

i 1

1

15 59,5 16 64,5 6 69,5 6 74,5)

5580 55,8.

100

И

Смещенная и состоятельная оценка дисперсии – статистическая

дисперсия:

Д

1 k

1

2

2

2

D

(х x

)

n

(3 (34,5 55,8)

3 (39,5 55,8)

100

B

ni 1

i

В

i

А

16 (44,5 55,8)2

22 (49,5 55,8)2

15 (54,5 55,8)2 16 (59,5 55,8)2

6 (64,5 55,8)2 6 (69,5 55,8)2

6 (74,5 55,8)2) 92,23.

б

Несмещенная и состоятельная оценка дисперсии – исправленная

выборочная дисперсия: S2

n

DB 93,1.

Смещенная

n 1

оценка

среднего квадратического

состоятельная

отклонения

С

среднее

квадратическое

отклонение:

–

выборочное

В

DВ

9,604.

Несмещенная иисостоятельная оценка среднего квадратического

отклонения

–

исправленное

среднее

квадратическое

отклонение

(стандарт): S

S2

9,64.

93,1

x

t

S

;

x

t

S

.

Зададимся доверительной

вероятностью

n

n

n 1 99, по

0,95

и, учитывая,

что число степеней свободы

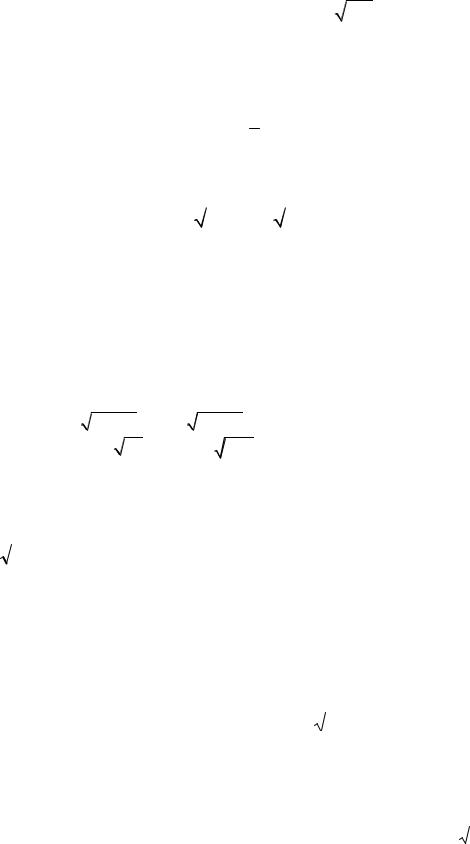
Точность

оценки

равна

1,98

9,64

1,91.

Тогда

100

55,8 1,91 a 55,8 1,91

и

доверительный

интервал

примет

вид

(53,89; 57,71).

Определяем величину относительной ошибки подсчета

среднестатистического значения: q

100 %

1,91

100 % 3,4 %.

x

В

55,8

Построим доверительный интервал для среднего квадратического

отклонения. Так

как математическое

ожидание

неизвестно,

то

S

S

n 1

n 1

2

2

оцениваемый

параметр

;

, где

1

1

;

2

1

2

,n 1

2

2

– квантили

И

2 -распределения с

n степенями свободы.

2

1

,n 1

2

Д

Найдем

значения

квантилей

прил.

4.

Имеем

по

2

2

2

16,8;

2

2

2

47.

1

1 0,95

,100 1

0,98;99

2

1 0,95

,100 1

0,025;99

2

2

отклонения

Доверительный интервал для среднего квадратического

будет иметь вид

9,64

;

9,64

100 1

100 1

или (6,99; 11,7).

47

16,8

3. Проведем выравнивание статистического ряда по нормальному

закону

распределен

я,

функцияАплотности

которого

имеет

вид

1

(x a)2

б

С

f (x)

e

.

Оцен м

по

выборке параметры

нормального

2

закона распределенияиа и . По методу моментов в качестве оценок

а

и

примем соответственно выборочную среднюю

55,8 и

xВ

исправленное

выборочное

среднее

квадратическое

отклонение

S 9,64.

Заменяя

а

и

найденными

оценками,

получаем

вид

1

(x 55,8)2

2

теоретического закона распределения

f (x)

e

2 9,64 .

2 9,64

нормированной нормальной случайной величины t

1

e

t2

2

,

2

и (

)t связаны между собой соотношением

f x

1

t . Принимая

(t )

xi xB

i

S

, вычисляем значения

, где

t

i

;

x

f xi

S

S

i – середина

i-го разряда. Вычисления сведем во вспомогательной таблице:

xi ;xi 1

[32;37)

[37;42)

[42;47)

[47;52)

[52;57)

[57;62)

[62,67)

[67;72)

[72;77]

~

34,5

39,5

44,5

49,5

54,5

59,5

64,5

69,5

74,5

xi

ti

-2,22

-1,70

-1,18

-0,66

-0,14

0,39

0,91

1,43

1,95

(ti )

0,033

0,094

0,199

0,321

0,396

0,37

0,264

0,144

0,06

~

0,004

0,010

0,021

0,033

0,041

0,039

0,028

0,015

0,006

f xi

Находим

теоретические

вероятности

рi

и

выравнивающие

частоты ni npi 100pi . Теоретические вероятности

pi вычисляем

по приближенной формуле

pi

~

i,

где

i

длина i-го разряда.

f xi

Их вычисление представим в таблице:

xi ;xi 1

[32;37)

[37;42)

[42;47)

[47;52)

[52;57)

[57;62)

[62,67)

[67;72)

[72;77]

И

ni

3

3

13

16

22

15 16

6

6

pi

0,02

0,05

0,105

0,165

0,205

0,195

0,140

0,075

0,030

Д

ni

2

5

10,5

16,5

20,5 19,5

14

7,5

3

совокупности,

то

теоретические

вероятности

можно найти

по

x

x

B

x

x

B

формуле pi P xi

X

xi 1 Ф

i 1

Ф

i

, где Ф(х)

–

S

С

S

функция Лапласа (см. прил. 2).

Имеем

55,8;

S 9,604.

хВ

p P X 37 Ф

37 55,8

Ф

55,8

Ф( 2) Ф( )

1

9,604

9,604

0,4773 0,5 0,022;

p P 37 X 42

Ф

42 55,8

Ф

37 55,8

Ф( 1,53) Ф( 2)

2

9,604

9,604