Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Сибирская государственная автомобильно-дорожная академия

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

788

.pdf

Скачиваний:

Добавлен:

07.01.2021

Размер:

684.5 Кб

Скачать

☆

<<< < Предыдущая 12 / 42 3 4 > Следующая >>>

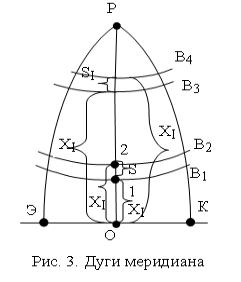
В2 = 45˚02'34", 8726;

В1 =33˚01'18",2632.

По широтам B1, B2, B3 и B4 найти дуги меридиана X от экватора до точек с заданными широтами по формулам

X = a0 B −

sin 2B +

sin B −

sin B +...

= m −

3 m +

m , m = a(1−e2 );

15 m ,

m =

3 e2m

;

(7)

m , m =

5 e2m

;

m = 7 e2m

или

X =

B −

n −

sin 2B +

−

sin 4B −

sin 6B

1+ n

n =

α2

α3

α4

(8)

4 + 8 +

16 =

2 f −1

a – ольшая полуось эллипсоида; α –

где

бсжатие; f – знаменатель сжатия.

На рис. 3 дуги меридианов обозначе-

ны как ХII и ХI. Разность Х равна дуге в

метрах между соответствующими точками.

Эта же дуга вычислена, кроме того, как BI"

в секундах. Таким же образом найдём дугу

SII

в метрах и BII" в секундах.

При разности широт в пределах не-

скольких градусов длину дуги

X найти по способу Симпсона (9).

∆X =

Bm − B0 (M0 + M m + 4(M1 + M3 +... + M m−1 )+

+ 2(M 2 + M 4 +... + M m−2 )),

(9)

где B0 и Bm – широты начальной и конечной точек дуги меридиана;

Mi – радиус кривизны меридиана в заданной точке вычисляют по формуле (1);

m – число равных интервалов, на которое делят дугу меридиана (m – чётное число).

При вычислениях дугу делят на 8 равных интервалов, находят широты промежуточных точек и радиусы кривизны меридиана в этих точках. Первую точку считают нулевой. Значения широт в формуле

(9) выражают в радианах.

По формулам (7) или (8) вычислить дуги меридиана от экват ора до заданных точек для эллипсоида Ф. Н. Красовского и ГСК–2011 г.

Вычислить разности дуг.

По формулам Симпсона (9) с учётом (1) вычислить дуги второй

раз.	К сдаче представить:	И

– два варианта вычисления дуг, расхождения между вариантами для эллипсоида Ф. Н. Красовского, Д

– два варианта вычисления дуг, расхождения между вариантами для эллипсоида ГСК–2011.

Контрольные вопросы и задания

1.Как вычислить длиныбдуг меридианов?

2.Как рассчитатьидлины дуг от экватора до каждой из четырех

точек?

3.Что такоеСвысшая геодезия?

4.Напишите формулу С мпсона.АРешение геодезических задач

на поверхности земного эллипсоида

Цель: научиться решать геодезические задачи на поверхности земного эллипсоида.

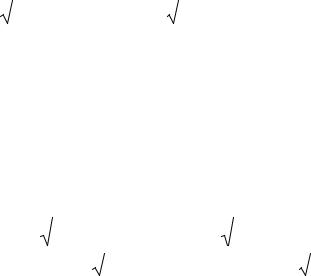
Главные геодезические задачи, решаемые методами сфероидической геодезии, позволяют определить геодезические координаты B и L некоторой точки или длину геодезической линии и ее азимут на поверхности эллипсоида (рис. 4).

Решение ГГЗ для пунктов P и Q сводится к решению сфероидического треугольнка PDQ. При решении ПГЗ известными являются

					P	сторона DR = 900 – B1, длина геодезиче-
						ской линии s и азимут этой линии A1. При
				L		решении ОГЗ известными являются сто-
						роны DR = 900 – B1, DQ = 900 – B2 и угол
						∆L = L2 − L1 . Следовательно,	решение
						ГГЗ в свете сфероидической геодезии за-
					A2-1	ключается в вычислении двух углов и
						стороны сфероидического треугольника,

	A1-2
				Q2 (B2, L2)		по известным двум его сторонам и углу
		Q1 (B1, L1)
		Q1 (B1, L1)
						между ними.
			Рис. 4. Полярный			между ними.
			Рис. 4. Полярный			Формулы сферической тригономет-
сфероидический треугольник						И	решения
сфероидический треугольник						рии используются только для	решения

треугольника на шаре, поэтому для решения сфероидического треугольника используются специальные приемы.

щего ему сферического треугольникаД, который решают по формулам сферической тригонометрии. Затем выполняется обратный переход с

Прием 1. Прямой путь решения, при котором используется ка-

кая-либо проекция поверхности эллипсоида на шар. По трем элемен-

там сфероидического треугольника находят элементы соответствую-

шара на эллипсоид. Одной из лучных реализаций этого приема счита-
ется способ Бесселя.		А
Прием 2. Косвенный путь решения предполагает нахождение
	б
приращений геодез ческ х координат и азимута, от которых осуще-
и
С

ствляется переход к скомым величинам. Этот прием был распространен для решения ГГЗ для рядов триангуляции при построении АГС в XX столетии. В связи с развитием принципиально новых методов создания ГГЗ и вычислительной техники этот прием потерял актуальность.

Прием 3. Сводится к редуцированию исходных величин на плоскость в некоторой проекции, например в проекции Гаусса– Крюгера. ГГЗ решаются по формулам плоской тригонометрии, после чего выполняется обратное редуцирование.

Прием 4. Решение ГГЗ в пространстве. Для этого от известных величин на поверхности эллипсоида переходят к их значениям в пространственной прямоугольной системе координат. Дальнейшие вычисления ведутся по формулам аналитической геометрии с обратным преобразованием найденных элементов на поверхность эллипсоида.

Прямая геодезическая задача

Исходные данные: геодезические координаты B1 и L1 точки Q1 ,а также азимут A1-2 с точки Q1 на точку Q2 и расстояние S между пунк-

тами Q1 и Q2 (рис.4).

Требуется определить широту B2 и долготу L2 точки Q2 и обратный азимут A2-1 с точки Q2 на точку Q1.

Прямая геодезическая задача решается главным образом при вычислении геодезических координат пунктов триангуляции 1 класса. Зная координаты начального пункта, а также расстояния и азимуты на соседние пункты, вычисляют геодезические координаты и обратные азимуты для всех других пунктов, непосредственно связанных с на-

чальным пунктом.

Исходные данные: по своему порядковому номеру в списке

журнала преподавателя из табл. 4 взятьВ1

; L1;S и А1 2 ..

Задание

Вычислить геодезические координаты L1

и L2

и обратный ази-

мут А21

с пункта Q2

на пункт Q1.

Порядок выполнения задания

Порядок решен я прямой геодезической задачи по способу

Бесселя на эллипсо де Ф. Н. Красовского

Исходными данными являются широта B1, долгота L1, длина

геодезической линии s и азимут A1

этой линии в начальной точке. Не-

обходимо найти широту B2

и долготу L2

конечной точки и обратный

азимут A2 в этойСточке. При вычислениях угловые величины необхо-

димо выражать в радианах.

Вычисляем приведённую широту начальной точки

tgU1

sinU

; cosU

; tgU

1−e2tgB

. (10)

1+tg2U1

2. Для перехода от s к σ найдём вспомогательные величины A0 и σ1 по формулам

tgα =

tgU1

, tgA = sin A1 cos A1 .

(11)

cosA1

tgU1

Введём обозначение k 2 = +e′2 cos A0

и вычислим коэффициенты

α, β, γ по формулам (12) и α1, β1

по формулам (13)

A =1+ k 2

−

4 +

k6 −...;

256

B = k 2

− k 4

−...;

512

k 4 4

C =

+512k6

...;

128

k 2

;

α =

−

1−

256

+...

4 4

β = B = k

− k

−...

;

512

k 4

А−

+...

;

(12)

γ =

128

б6

A0 −

;

(13)

β1 =

... cos

+... cos

σ = αS + βsin σcos(2σ1 +σ)+ γsin 2σcos(4σ1 + 2σ +...) .

(14)

За первое приближение примем σ0 = αS . Примем обозначения

Iσ = βsin σ0 cos(2σ1 +σ0 ); IIσ = γsin 2σ0 cos(4σ1 +σ0 ); IIIσ = Iσβcos(2σ1 +σ0 ).

Для вычисления σ" с погрешностью менее 0,001" получили формулу

σ = σ0 + Iσ + IIσ + IIIσ.

(15)

Находим сферическое расстояние σ по формуле и затем σ2 = σ1 + σ. Решаем прямую задачу на шаре по формулам

tgλ1 = sin A0tgσ1 ;						tgλ2 = sin A0tgσ2 ;
tgA =		tgA0		;	tgU		2	= −cos A tgσ		2	;
tgA =				;	tgU			= −cos A tgσ			;
2		cos σ2							2
		cos σ2
					λ = λ2 − λ1.						(16)
Далее вычислим разность долгот								И
								И
l = λ−sin A0 (α1σ + β1 sin σcos 2σ1									+σ).		(17)
	2				Д2
Вычисляем геодезическую широту конечной точки
			А
	б				′2
	tgB = 1+e tgU

и геодезическую долготуиL2=L1+ l.

Способ Бесселя по простоте и строгости решения превосходит любые другие,Си его можно пр менять при любых расстояниях между точками на эллипсо де. Погрешности по способу Бесселя зависят от количества верных значащих цифр, удерживаемых при вычислениях, так как ряды в формулах ( 14) и (17) быстро сходятся и могут быть вычислены с любой необходимой точностью.

При решении прямой геодезической задачи необходимо удерживать не менее девяти верных значащих цифр.

Решив прямую геодезическую задачу, получим координаты второго пункта Q2 геодезической линии Q1Q2, то есть В2 и L2 , которые

будут исходными данными для решения обратной геодезической задачи.

Обратная геодезическая задача

К решению обратной геодезической задачи прибегали в некоторых методах уравнивания полигонов триангуляции 1-го класса. В прошлом различали:

1.Малые расстояния до 30–45 км.

2.Средние расстояния до 600 км.

3.Большие – до 5 000 км.

4.Очень большие – до 19 000–20 000 км.

В настоящее время для решения прямой и обратной геодезической задачи на эллипсоиде целесообразнее применять способ Бесселя. Точность получения прямого и обратного азимута и расстояния между пунктами Q1 и Q2 геодезической линии будут зависеть от погрешностей применяемого математического аппарата, исходных данных и

погрешностей вычислений.								Д
Рассмотрим решение обратной геодезической задачи.
Исходные данные: В1 ; L1					и В2 ; L2			; требуется получить S1 2 ; А21		и
А1 2 .					А				И
			Порядок выполнения задания
				б
Решение обратной геодезической задачи на эллипсоиде по спо-
			и
собу Бесселя сложнее прямой задачи, так как по исходным данным
можно вычислить на шаре только приведённые широты U1 и U2										по
С					tgU			1−e2 tgB .
формулам tgU	1	=	1−e2 tgB ;		tgU	2	=	1−e2 tgB .
	1			1		2			2

Предварительные вычисления

Разность долгот l выражается в радианах.

Для определения долготы λ на шаре необходимо знать A0, σ1 и δ, которые зависят от s и A1. Следовательно, применим последовательные приближения.

W =

1−e2 sin2 B

;

W =

1−e2 sin2 B

;

sin B

1−e2

sin B

1−e2

sin u1 =

;

sin u2

;

cosu	= cos B1 ; cosu	2	= cos B2 ; l = L	− L		;
1	W1	2	2	1
	W1		W2
	a1 = sin u1 sin u2 ;		a2 = cosu1 cosu2 ;
	b1 = cosu1 sin u2 ;		b1 = sin u1 cosu2 .
	λ= l+ δ.
В первом приближении принимаем δ = 0 радиан.
p = cosu2 sin λ; q = b1 −b2 cos λ; A1′ = arccos					q		;

					p2	+ q2
					p2	+ q2

(18)

(19)

(20)

(21)

′

если p > 0 или A1 = 2

′

= 360

′

если p < 0.

где A1 = A1

π− A1

− A1

Вычисляем дугу на шаре

arccosσ = α1 +α2 cos λ

(22)

далее A0

и коэффициенты α,

β и поправку δ

sin A = cosu

sin A

;

cos

A =1

A cos σ

−sinДA ; x = 2 α −cos

cos2

e6 cos4 A ;

α =

−

A +

128

′

cos

;

δ = (α σ − β

′

x sin σ) sin A0 . (23)

−

Коэффициенты α,

β и поправку δ получаем в радианах.

Вычисленное значение δ подставляем в (20) и повторяем все вычисления по формулам (21), (22) и (2 3) и т.д. Приближения заканчиваем, когда δi −δi − 1 < 48·10-11.

Значения λ, A1, σ, x и sinA0, полученные в последнем приближении, принимаем за окончательные.

Вычисляем коэффициенты A, B', C' и геодезическую линию на эллипсоиде s.

Для нахождения коэффициентов A, B', C' возьмем формулы

k	2	′2	cos	2	A0	;	(24)
		= e

B′ = e′2


A =1+		k	2		3k 4			+	5k6	;
		4		−	64				256
− e′4
	cos2			A0	+		15		e′6 cos4 A0 ;
						512
16
	C′ =		e′4			3e′6
			64 −			128 .

(25)

(26)

(27)

Длину геодезической линии на эллипсоиде вычисляем по формулам

y = (cos4 A0 −2x2 ) cos σ ;

s = (A σ +(B′ x +C′ y) sin σ)

α 1−

(28)

где a – большая полуось эллипсоида, f – знаменатель сжатия.

Обратный азимут найдем из формул

p′ = cosu1 sin λ;

q′ = b1

cos

λ−b2 ;

q′

A2′

= arccos

;

(29)

′2

+ p

где A

′

=180

′

, если p'>0 или

′

= π+ A

+ A

A = π− A =180

− A , если

p'<0.

Погрешности выч сленбй прямой и обратной задач не превы-

шают 2 мм в коорд натах

в длинах линий и 0,001” в азимутах.

Контрольные вопросы и задания

1. Какие приемы используются для решения сфероидического треугольника?

2. Как решается прямая геодезическая задача?

3. Опишите порядок решения прямой геодезической задачи по способу Бесселя на эллипсоиде Ф. Н. Красовского.

4. Что такое обратная геодезическая задача?

Лабораторная работа 4

Вычисление прямоугольных координат Гаусса по геодезическим координатам и обратно, с вычислением

Гауссового сближения меридианов

Цель: вычислить прямоугольные координаты Гаусса по геодезическим координатам и обратно, с вычислением Гауссового сближения меридианов.

Необходимо вычислить прямоугольные координаты x и y в проекции Гаусса–Крюгера по геодезическим координатам B и L в системе СК–95 и ГСК–2011.

Каждый студент пользуется данными своего индивидуального задания, т. е. геодезическими координатами пункта. Индивидуальные задания составлены так, что все пункты находятся в полосах перекрытия шестиградусных зон. Шестиградусная зона проекции Гаусса– Крюгера представляет собой сфероидический двуугольник, построенный от одного полюса до друго-

	го и ограниченный меридиана-	И
	ми.	И
	ми.	Д
	В каждой зоне изображе-
	ние осевого меридиана прини-

мается за ось абсцисс,	а изо ра-
жение экватора за ось ординат.
	А
В проекции Гаусса–Крюгера
осевой меридиан	экваторб

изображаютсяСпрямымиил н я- ми. В каждой зоне имеется своё начало координат – это проекция точки пересечения осевого меридиана с экватором на плоскость в проекции Гаусса.

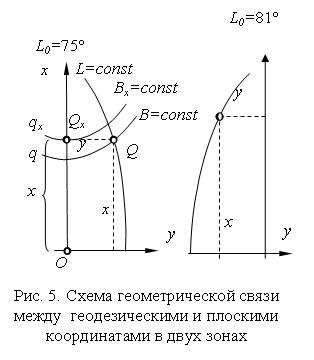
Точка а (рис. 5) − изображение точки А (эллипсоида) на

плоскости. Положение a определяется прямоугольными координатами x и y. Каждый студент вычисляет координаты точек от осевых меридианов двух смежных зон, например от осевого меридиана

75˚ и 81˚.

Исходные данные: Для точки с геодезическими координатами В1 и L1, которые выбирают из табл. 4, по номеру студента в журнале

<<< < Предыдущая 12 / 42 3 4 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
07.01.2021682.98 Кб1783.pdf
#
07.01.2021683.26 Кб1784.pdf
#
07.01.2021683.26 Кб3785.pdf
#
07.01.2021683.36 Кб2786.pdf
#
07.01.2021683.36 Кб0787.pdf
#
07.01.2021684.5 Кб1788.pdf
#
07.01.2021685.57 Кб0789.pdf
#
07.01.2021279.07 Кб079.pdf
#
07.01.2021685.93 Кб7790.pdf
#
07.01.2021686.11 Кб1791.pdf
#
07.01.2021686.65 Кб4792.pdf