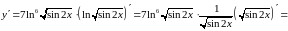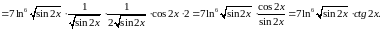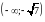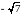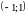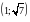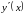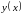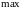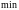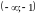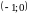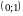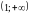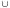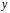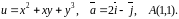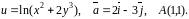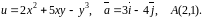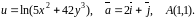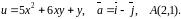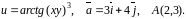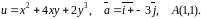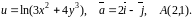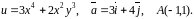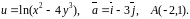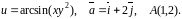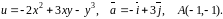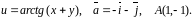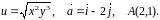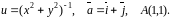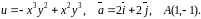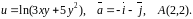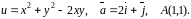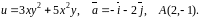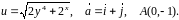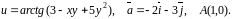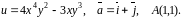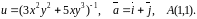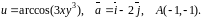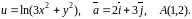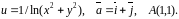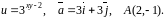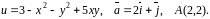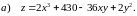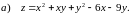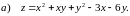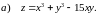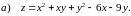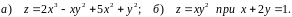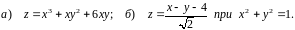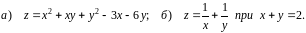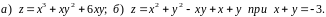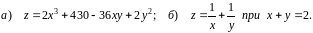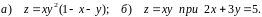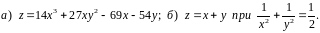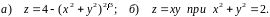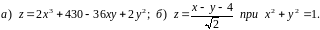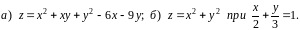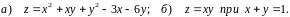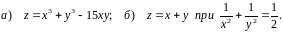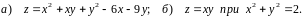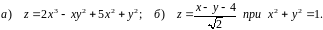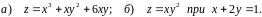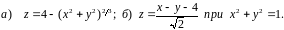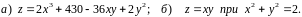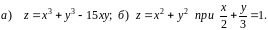Область визначення функції: .
Дослідимо функцію на парність:
Отже, не виконуються ні рівність , ні , тому дана функція загального вигляду.
Знайдемо точки перетину графіка функції з осями координат:
а) в точці функція не визначена, отже крива не перетинає вісь ординат;
б) . Графік функції перетинає вісь абсцис в точці (1,0);
Знайдемо точки розриву функції і асимптоти.
а) Оскільки , то точка - точка розриву другого роду. Рівняння вертикальної асимптоти: .
б) Рівняння похилої асимптоти шукаємо у вигляді :
Отже, рівняння – рівняння похилої асимптоти.
в)
Оскільки
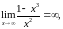 то горизонтальних асимптот немає.
то горизонтальних асимптот немає.
5) Щоб визначити інтервали монотонності і точки екстремуму функції , знайдемо першу похідну:
Маємо
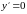 ,
якщо
–
стаціонарна точка. У точці
функція і її похідна не визначені.
Розділяємо область визначення функції
на проміжки. Дослідимо знак похідної
на кожному проміжку. За знаком першої
похідної визначимо проміжки монотонності
функції та знайдемо точки екстремуму.
,
якщо
–
стаціонарна точка. У точці
функція і її похідна не визначені.
Розділяємо область визначення функції
на проміжки. Дослідимо знак похідної
на кожному проміжку. За знаком першої
похідної визначимо проміжки монотонності
функції та знайдемо точки екстремуму.
а) , – функція спадає;
б) , похідна – функція зростає. При переході через точку похідна змінює знак мінус на плюс. Тому в цій точці – мінімум:
В околі точки похідна змінює знак плюс на мінус. Проте зробити висновок, що в точці функція має максимум, неможливо, оскільки в цій точці функція не визначена.
Зведемо одержану інформацію в таблицю
-
0
–
0
+
Не визнач.
–
Не визнач.
Знайдемо інтервали опуклості і угнутості графіка функції. Знайдемо
Критична точка другого роду . Розбиваємо область існування функції на інтервали: Знак другої похідної і інтервали опуклості і угнутості графіка функції зображено на рисунку
Рис. 1.
Оскільки у точці функція і її похідні не визначені, графік функції немає перегину.
За результатами проведеного дослідження побудуємо графік функції
Рис. 2.
Задача №3.
Провести
повне дослідження і побудувати графік
функції
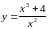 .
.
Розв’язання.
1)
Область визначення функції - вся вісь
Ох, за винятком точки х = 0, тобто
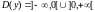 .
.
2)
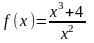 ,
,
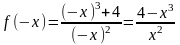 .
.
 ,
,
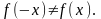
Функція не є ні парною, ні непарною.
3)
Знайдемо точки перетину графіка з віссю
Ох, маємо
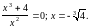
4)
Точка розриву х = 0, причому
 отже, х = 0 (вісь Оy) є вертикальною
асимптотою графіка.
отже, х = 0 (вісь Оy) є вертикальною
асимптотою графіка.
Знайдемо
невертикальні асимптоти:
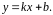
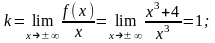
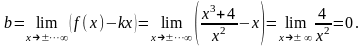
Таким
чином, рівняння похилої асимптоти має
вигляд
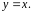
5) Знайдемо екстремуми й інтервали зростання та спадання функції. Для цього знайдемо першу похідну функції
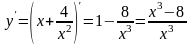
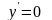 при
при

Точки
х = 0 і х = 2 розбивають числову вісь на
проміжки
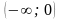 ;
;
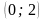 ;
;
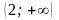 ,
,
-

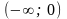
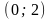
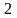
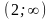
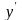
+
–
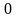
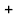
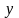
зростає
спадає
3
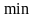
зростає
6) Знайдемо інтервали опуклості і точки перегину.
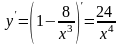
Оскільки
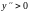 при всіх
з області визначення, то графік функції
є угнутим на кожному інтервалі області
визначення. Точок перегину крива не
має.
при всіх
з області визначення, то графік функції
є угнутим на кожному інтервалі області
визначення. Точок перегину крива не
має.
7) Використовуючи ці дані, будуємо графік функції (Рис. 1).
Р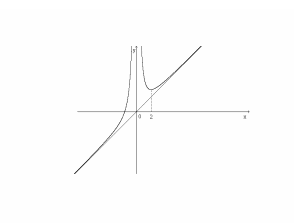 ис.
1.
ис.
1.
Задача
№8. За
допомогою методів диференціального
числення дослідити функцію
 та побудувати ії графік.
та побудувати ії графік.
Розв’язання. За допомогою методів диференціального числення дослідити функцію та побудувати її графік:
Дослідимо поведінку функції згідно схеми [ч.1, c. 412]:
1)
Область визначення:
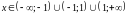 ;
;
2)
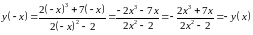 ,
отже функція є непарною і її графік
симетричний відносно початку координат
,
отже функція є непарною і її графік
симетричний відносно початку координат
Рівняння
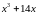 має один дійсний корінь
має один дійсний корінь
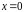 ,
отже графік функції перетинає координатні
осі лише в початку координат.
,
отже графік функції перетинає координатні
осі лише в початку координат.
Точки
розриву
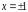 ,
причому
,
причому
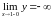 ;
;
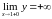 ,
,
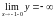 ;
,
;
,
отже,
прямі
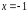 ,
,
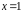 є вертикальними асимптотами графіка.
Знайдемо похилі асимптоти [1, с. 411]:
є вертикальними асимптотами графіка.
Знайдемо похилі асимптоти [1, с. 411]:
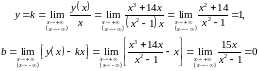
Таким
чином, рівняння похилої асимптоти
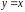 .
.
4) Для знаходження точок можливого екстремуму обчислимо першу похідну функції:
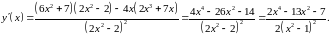
Похідна існує в усій області визначення функції. Тому екстремум функції може бути тільки в стаціонарних точках. Для знаходження стаціонарних точок похідну функції прирівняємо до нуля.
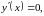
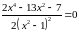 .
.
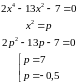 .
.
 ;
;
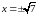
Точки стаціонарні. Вони розбивають область визначення функції на інтервали, як показано в таблиці
|
|
|
|
|
|
|
|
|
+ |
0 |
- |
- |
- |
0 |
+ |
|
|
|
|
|
|
|
|
5) Визначимо інтервали опуклості, угнутості, а також точки перегину [1, стр. 408-409]. Для цього необхідно знайти другу похідну функції:
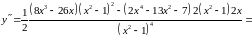
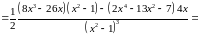
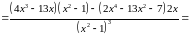
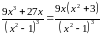
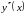 обертається
на нуль лише при
.
Будуємо таблицю знаків другої похідної
та проміжків опуклості - вгнутості
заданої функції
обертається
на нуль лише при
.
Будуємо таблицю знаків другої похідної
та проміжків опуклості - вгнутості
заданої функції
|
|
|
0 |
|
|
|
- |
- |
0 |
- |
+ |
|
|
|
т. перегину |
|
|
6)
Використовуючи отримані дані, будуємо
графік функції та її асимптот.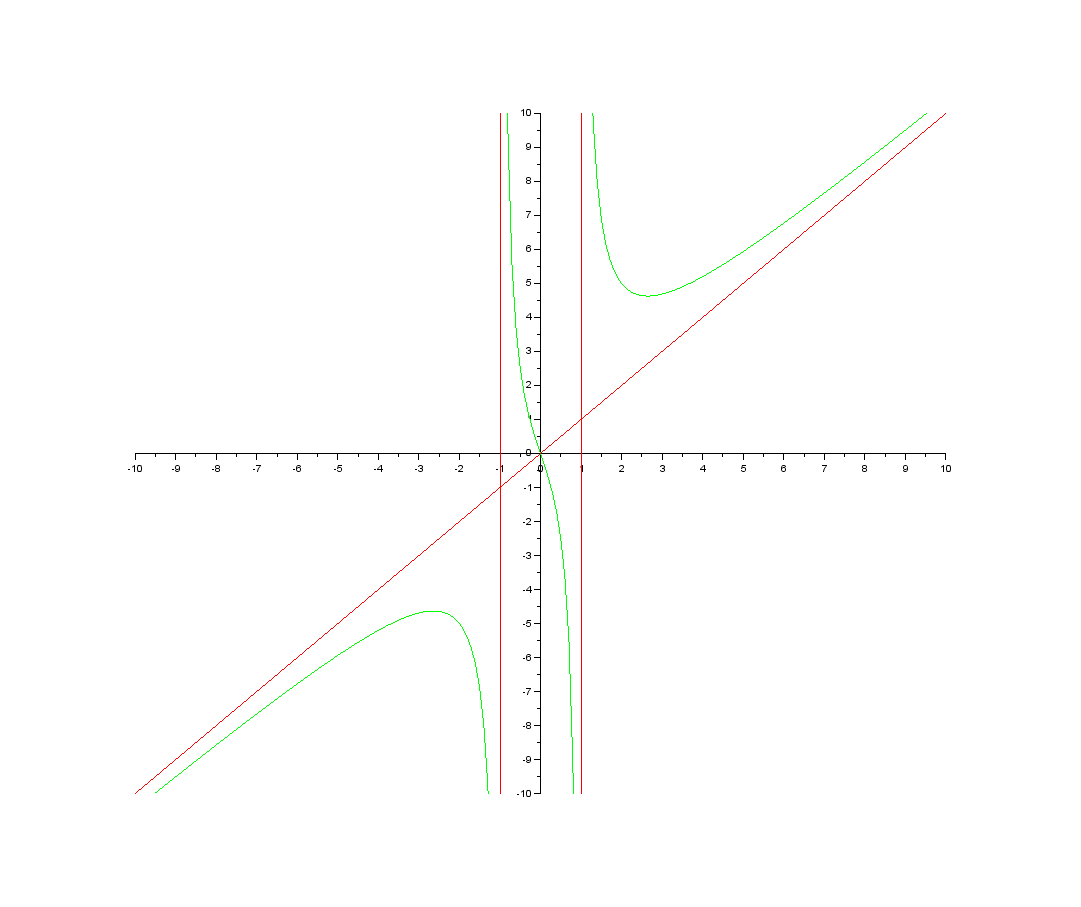




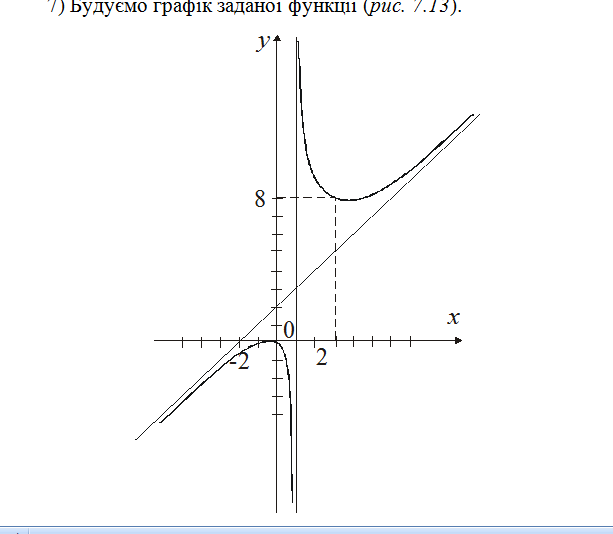
Рис. 7.13
Задача №4.
Знайти
градієнт функції
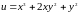 та похідну функції за напрямком вектора
у точці
.
та похідну функції за напрямком вектора
у точці
.
Розв’язання. За визначенням [1,с.372]
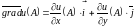
Знайдемо частинні похідні першого порядку:
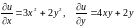 .
.
Обчислимо
їх значення в точці
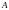 :
:
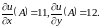
Тоді
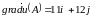 .
.
Похідна функції за напрямком вектора дорівнює [1,с.371]
,
де
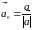 - орт вектора
- орт вектора
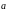 .
.
Для заданого вектора знаходим
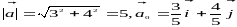 .
.
Тоді
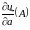 =
=
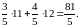
Задача
№3.

Знайти
градієнт функції
 та похідну функції за напрямком вектора
та похідну функції за напрямком вектора
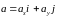 в точці
в точці
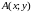 ;
г)дослідити функцію
;
г)дослідити функцію
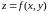 на екстремум.
на екстремум.
в)
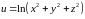 ,
,
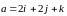 ,
,
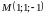 ;
;
г)
 .
.
Розв’язання.
За формулою [ч.1, с. 372],
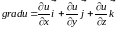
Для
обчислення градієнта функції
знайдемо її частині похідні у точці
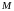 :
:
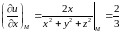 ;
;
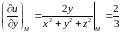 ;
;
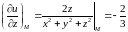 .
.
Тоді
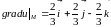
Похідну функції за напрямом вектора в точці обчислимо за формулою (23.1) [ч.1,с.372]
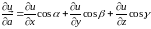 ,
,
де
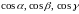 – напрямні косинуси вектора
.
– напрямні косинуси вектора
.
Знаходимо напрямні косинуси вектора , довжина якого
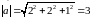
Маємо
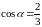 ,
,
 ,
,
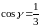 .
.
Тому
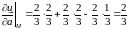 .
.
г) Задана функція є визначеною і диференційованою для всіх . Тому екстремум може бути тільки у стаціонарних точках [ч.1, с. 403]. Щоб знайти стаціонарні точки, розв’яжемо систему
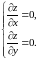
Знайдемо частині похідні
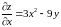 ,
,
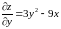 .
.
Отримаємо систему
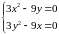
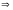
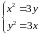
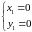 і
і
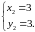
Розв’язавши
останню систему, знаходимо дві стаціонарні
точки:
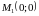 ,
,
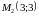 .
Для того, щоб скористатися достатньою
умовою екстремуму [ч.1,
с. 423],
знайдемо частинні похідні другого
порядку в цих точках:
.
Для того, щоб скористатися достатньою
умовою екстремуму [ч.1,
с. 423],
знайдемо частинні похідні другого
порядку в цих точках:
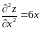 ,
,
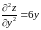 ,
,
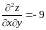 .
.
Перевіримо достатні умови для точки :
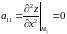 ,
,
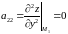 ,
,
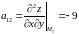
Оскільки
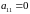 і
і
 ,
то згідно з умовою [ч.1,
с.424],
,
то згідно з умовою [ч.1,
с.424],
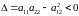 і в точці
екстремуму немає.
і в точці
екстремуму немає.
Відповідно для точки :
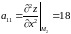 ,
,
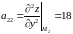 ,
,
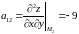
Тобто
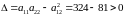 ,
,
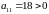
Тоді відповідно до умови [ч.1, с.424], в точці є екстремум і це мінімум.
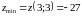 .
.
г) дослідити функцію на екстремум.
г) .
г)
Задача
№10. а) Дослідити
функцію
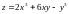 на екстремум.
на екстремум.
Розв’язання. Знайдемо частинні похідні першого порядку:
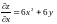 ,
,
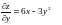 .
.
Оскількі
похідні визначені при всіх значеннях
 і
і
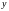 ,
то екстремуми можуть бути тількі у
стаціонарних точках. Знайдемо стаціонарні
точки данної функції
[1,с.404].
Для
цього розв’яжемо
систему
,
то екстремуми можуть бути тількі у
стаціонарних точках. Знайдемо стаціонарні
точки данної функції
[1,с.404].
Для
цього розв’яжемо
систему
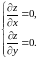
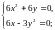
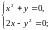
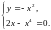
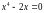 ,
,
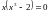 ,
,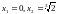 ,
,
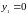 ,
,
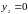 .
Функція має дві стаціонарні точки:
.
Функція має дві стаціонарні точки:
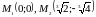 .
.
Для перевірки достатніх умов [ч.1,с.422] знайдемо частинні похідні другого порядку:
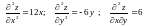 .
.
Обчислимо
їх значення в точці
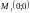 :
:
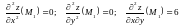 .
.
Перевіримо достатні умови :
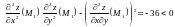 .
.
Отже, екстремуму в точці немає.
Для
точки
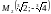 :
:
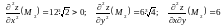 ;
;
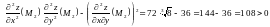 .
.
Отже, точка є точкою мінімуму.
Задача
№2.
Знайти
найбільше та найменше значення функції
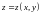 в області, яка обмежена заданими лініями.
Зобразити задану область.
в області, яка обмежена заданими лініями.
Зобразити задану область.
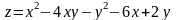
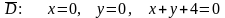
Найбільше
та найменше значення функції в замкнутій
області знаходяться в критичних точках,
що належать даній області, або на її
межі. Таким чином,
правило знахождення
найбільшого
та
найменшого
значень
диференційовної
в області
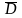 функції
функції
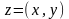 полягає
у слідуючому::
полягає
у слідуючому::
1) Знайти всі критичні точки функції, що належать , та обчислити в знайдених точках значення функції.
2) Знайти найбільше та найменше значення функції на границях області.
3)
Порівняти
всі
знайденні
значення
функції
та
обрати
з них найбільше
М і
найменше
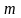 .
.
Розв’язання. Зобразимо вказану область
Знайдемо точки перетину прямих. Граничні точки області:
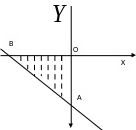
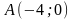 ,
,
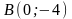 ,
,
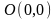
Для знаходження усіх критичних точок функції розв’яжемо систему:
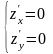
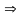
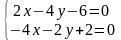
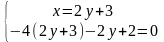
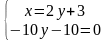
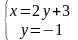
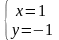
Критична
точка
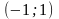 не
належить
вказаній
області,
отже, значення
фукнції
в ній
не береться
до уваги.
Далі дослідимо функцію на границі
області
:
не
належить
вказаній
області,
отже, значення
фукнції
в ній
не береться
до уваги.
Далі дослідимо функцію на границі
області
:
1)
На відрізку
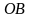
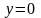 ,
,
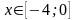
Після
підстановки
отримаємо функцію однієї змінної
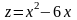 ,
яка досягає свого найбільшого (найменшого)
значення на кінцях проміжку або в його
критичних точках. Знайдемо
критичні
точки функції:
,
яка досягає свого найбільшого (найменшого)
значення на кінцях проміжку або в його
критичних точках. Знайдемо
критичні
точки функції:
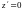 ,
,
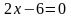 ,
,
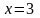
Оскільки
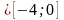 ,
то знаходимо значення функції тільки
на кінцях інтервалу:
,
то знаходимо значення функції тільки
на кінцях інтервалу:
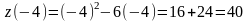 ,
,
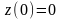 .
.
2)
На відрізку
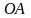
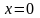
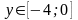
Виконаємо
вказану
підстановку:
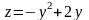 .
.
Знайдемо критичні точки:
,
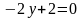 ,
,
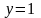
Знаходимо значення функції на кінцях :
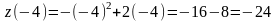 ,
,
3)
На відрізку

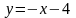 ,
,
=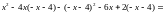
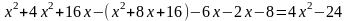
Знайдемо критичні точки:
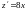 ,
,
 ,
,
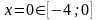
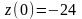
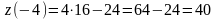
Отже, 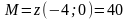 -
найбільше
значення
функції
в
області
,
-
найбільше
значення
функції
в
області
,
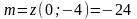 -
найменше
значення
функції
в
області
.
-
найменше
значення
функції
в
області
.
Задача
№11. За
експериментальними даними методом
найменших квадратів знайти коефіцієнти
 і
і
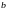 у
рівнянні
у
рівнянні
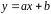 .
.
|
1 |
2 |
3 |
4 |
|
3 |
4 |
2,5 |
0,5 |
Розв’язання.
Для
знаходження коефіцієнтів
і
складемо та розв’яжемо систему рівнянь
 [ч.1, с.431].
Обчислимо
суми:
[ч.1, с.431].
Обчислимо
суми:
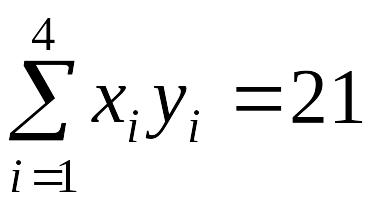 ,
,
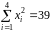 ,
,
 ,
,
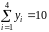 .
Отже, задана система набуває вигляду
.
Отже, задана система набуває вигляду
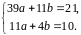 Звідки знаходимо:
Звідки знаходимо:
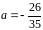 ,
,
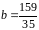 .
.
Задача
№8. За
допомогою методів диференціального
числення дослідити функцію
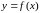 та побудувати ії графік.
та побудувати ії графік.
1.
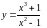 . 16.
. 16.
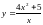 .
.
2.
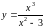 .
17.
.
17.
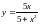 .
.
3.
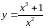 .
18.
.
18.
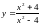 .
.
4.
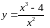 .
19.
.
19.
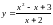 .
.
5.
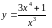 .
20.
.
20.
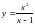 .
.
6.
 .
21.
.
21.
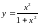 .
.
7.
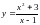 .
22.
.
22.
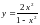 . .
. .
8.
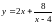 .
23.
.
23.
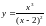 .
.
9.
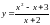 .
24.
.
24.
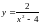 .
.
10.
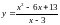 .
25.
.
25.
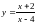 .
.
11.
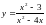 .
26.
.
26.
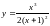 .
.
12.
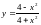 .
27.
.
27.
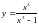 .
.
13.
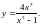 28.
28.
 .
.
14.
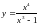 29.
29.
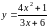 .
.
15.
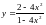 .
30.
.
30.
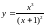 .
.
Задача
№9. Знайти
градієнт функції
![]() та похідну функції за напрямком вектора
та похідну функції за напрямком вектора
![]() у точці
у точці
![]() .
.
Задача
№2.
Задано функцію
 і вектор
і вектор
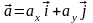 .
Знайти
.
Знайти
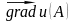 і похідну
цієї
функції
в
точці
А за напрямком вектора
і похідну
цієї
функції
в
точці
А за напрямком вектора
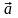 .
.
Варіанти №№1-10:
1.
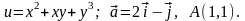
2.
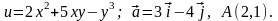
3.
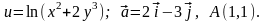
4.

5.
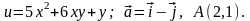
6.
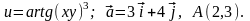
7.

8.
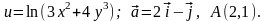
9.
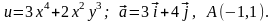
10.
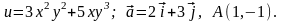
Задача№ 1. Дослідити функцію на екстремум.
Варіанти №№1-10:
1.
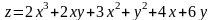
2.
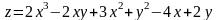
3.
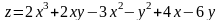
4.
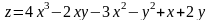
5.
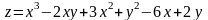
6.
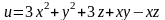
7.
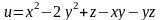
8.
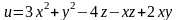
9.
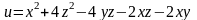
10.

Задача
№11. За
експериментальними даними методом
найменших квадратів знайти коефіцієнти
a
і b
в
рівнянні
![]() .
.
|
1 |
2 |
3 |
4 |
5 |
|
5,9 |
6,9 |
5,4 |
3,4 |
3,9 |
2.
|
1 |
2 |
3 |
4 |
5 |
|
5,7 |
6,7 |
5,2 |
3,2 |
3,7 |
3.
|
1 |
2 |
3 |
4 |
5 |
|
5,5 |
6,5 |
5,0 |
3,0 |
3,5 |
4.
|
1 |
2 |
3 |
4 |
5 |
|
5,2 |
6,2 |
4,7 |
2,7 |
3,2 |
5.
|
1 |
2 |
3 |
4 |
5 |
|
3,9 |
4,9 |
3,4 |
1,4 |
1,9 |
6.
|
1 |
2 |
3 |
4 |
5 |
|
4,7 |
5,7 |
4,2 |
2,2 |
2,7 |
7.
|
1 |
2 |
3 |
4 |
5 |
|
4,5 |
5,5 |
4,0 |
2,0 |
2,5 |
8.
|
1 |
2 |
3 |
4 |
5 |
|
5,9 |
6,9 |
5,4 |
3,4 |
3,9 |
9.
|
1 |
2 |
3 |
4 |
5 |
|
5,7 |
6,7 |
5,2 |
3,2 |
3,7 |
10.
|
1 |
2 |
3 |
4 |
5 |
|
5,5 |
6,5 |
5,0 |
3,0 |
3,5 |
11.
|
1 |
2 |
3 |
4 |
5 |
|
3,9 |
4,9 |
3,4 |
1,4 |
1,9 |
12.
|
1 |
2 |
3 |
4 |
5 |
|
5,1 |
6,1 |
4,6 |
2,6 |
3,1 |
13.
|
1 |
2 |
4 |
3 |
5 |
|
4,3 |
5,3 |
1,8 |
3,8 |
2,3 |
14.
|
1 |
2 |
3 |
4 |
5 |
|
4,7 |
5,7 |
4,2 |
2,2 |
2,7 |
15.
|
1 |
2 |
3 |
4 |
5 |
|
5,9 |
6,9 |
5,4 |
3,4 |
3,9 |
16.
|
1 |
2 |
3 |
4 |
5 |
|
5,2 |
6,2 |
4,7 |
2,7 |
3,2 |
17.
|
1 |
2 |
3 |
4 |
5 |
|
3,9 |
4,9 |
3,4 |
1,4 |
1,9 |
18.
|
1 |
2 |
3 |
4 |
5 |
|
5,1 |
6,1 |
4,6 |
2,6 |
3,1 |
19.
|
1 |
2 |
3 |
4 |
5 |
|
4,9 |
5,9 |
4,4 |
2,4 |
2,9 |
20.
|
1 |
2 |
3 |
4 |
5 |
|
4,7 |
5,7 |
4,2 |
2,2 |
2,7 |
21.
|
1 |
2 |
3 |
4 |
5 |
|
4,5 |
5,5 |
4,0 |
2,0 |
2,5 |
22.
|
1 |
2 |
3 |
4 |
5 |
|
4,3 |
5,3 |
3,8 |
1,8 |
2,3 |
23.
|
1 |
2 |
3 |
4 |
5 |
|
5,9 |
6,9 |
5,4 |
3,4 |
3,9 |
24.
|
1 |
2 |
3 |
4 |
5 |
|
4,5 |
5,5 |
4,0 |
2,0 |
2,5 |
25.
|
1 |
2 |
3 |
4 |
5 |
|
5,7 |
6,7 |
5,2 |
3,2 |
3,7 |
26.
|
1 |
2 |
3 |
4 |
5 |
|
3,9 |
4,9 |
3,4 |
1,4 |
1,9 |
27.
|
1 |
2 |
3 |
4 |
5 |
|
5,1 |
6,1 |
4,6 |
2,6 |
3,1 |
28.
|
1 |
2 |
3 |
4 |
5 |
|
4,3 |
5,3 |
3,8 |
1,8 |
2,3 |
29.
|
1 |
2 |
3 |
4 |
5 |
|
4,7 |
5,7 |
4,2 |
2,2 |
2,7 |
30.
|
1 |
2 |
3 |
4 |
5 |
|
5,5 |
6,5 |
5,0 |
3,0 |
3,5 |
а)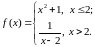
Розв’язання.
а)
Раціональна і дробово-раціональна
функції є неперервними в області
визначення, отже дана функція є неперервною
на всій числовій осі за винятком точки
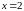 .
Дослідимо поведінку функції у вказаній
точці. Для цього обчислимо лівосторонню
та правосторонню границі. Так як зліва
і справа від цієї точки функція визначена
різними аналітичними виразами, то
.
Дослідимо поведінку функції у вказаній
точці. Для цього обчислимо лівосторонню
та правосторонню границі. Так як зліва
і справа від цієї точки функція визначена
різними аналітичними виразами, то
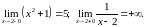
Оскільки
одна з границь є нескінченно великою,
то
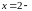 точка
розриву другого роду. Побудуємо графік:
точка
розриву другого роду. Побудуємо графік:
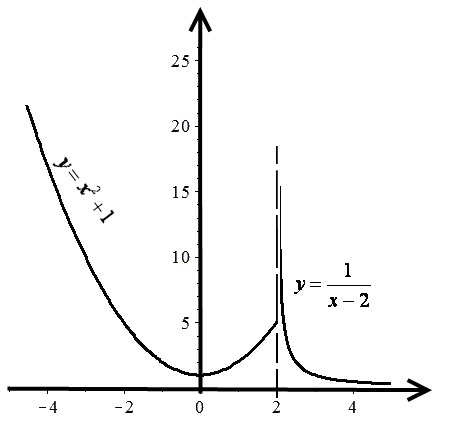

тобто,
точки
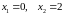 .
Обчислимо в цих точках односторонні
границі та значення даної функції.
Отримаємо:
.
Обчислимо в цих точках односторонні
границі та значення даної функції.
Отримаємо:
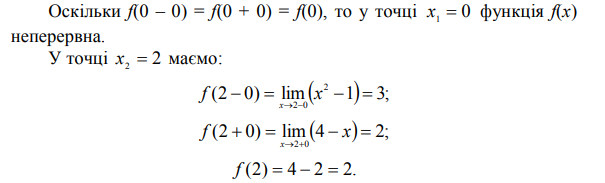


6)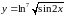
Розв’язання.
Маємо