Зразок_виконання_РГР_ВПМ_Тема_ЛА_та_АГ_копия_2

ЗРАЗОК ВИКОНАННЯ РГР

Тема «Лінійна алгебра та аналітична геометрія» (зад. 5-7)

Задача № 5. Розв’язати матричним методом балансове рівняння 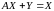, а саме, знаючи вектор кінцевого попиту 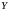та матрицю 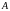прямих витрат, знайти матрицю повних витрат 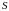та вектор валового продукту . , .

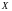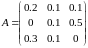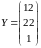Розв’язання.

Запишемо балансове рівняння у вигляді:

.

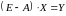Тоді розв’язок цього рівняння має вид:

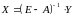або ,

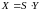де 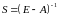– матриця повних витрат. Матрицю знайдемо за формулою:

.

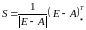Позначимо 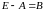та знайде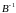мо . Маємо:

.

.

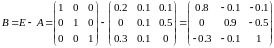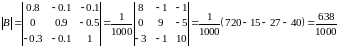Знайдемо союзну матрицю.

, , ,

, , ,

, , .

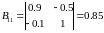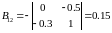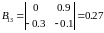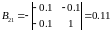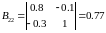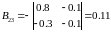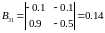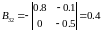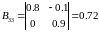Отже, .

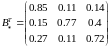Тоді 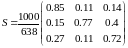матриця повних витрат.

Вектор валового продукту:

.

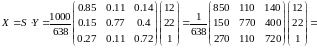
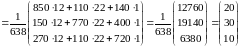_Отже, вектор валового продукту

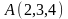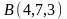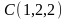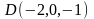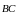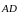Задача № 6. Вершини піраміди знаходяться в точках , , та . Обчислити: а) довжину ребра АС; б) скалярний добуток векторів та ; в) косинус кута 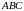; г) площу грані 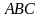; д) об’єм піраміди .

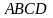Розв’язання.

а) 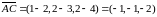, тоді довжина ребра АС дорівнює:

.

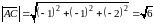б) Знайдемо координати вказаних векторів:

_Отже,

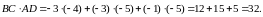
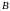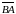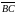в) Кут при вершині – це кут між векторами та . Маємо:

, .

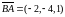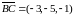Косинус кута між вказаними векторами дорівнює:

.

, .

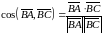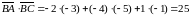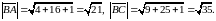Тоді:

.

г) Відомо, що 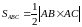. Знаходимо:

, ,

.

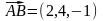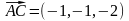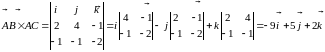Остаточно маємо:

.

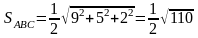д) Відомо, що .

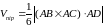Оскільки 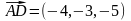, то

.

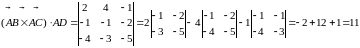Отже, .

Задача № 7. Вершини трикутника знаходяться в точках 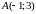, 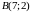і 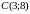. Знайти: а) рівняння та довжини сторін трикутника; б) кути трикутника; в) визначити тип трикутника (за сторонами та кутами); г) рівняння та довжину медіани ; д) рівняння та довжину висоти 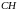; е) периметр та площу трикутника.

Розв’язання. Побудуємо даний трикутник.

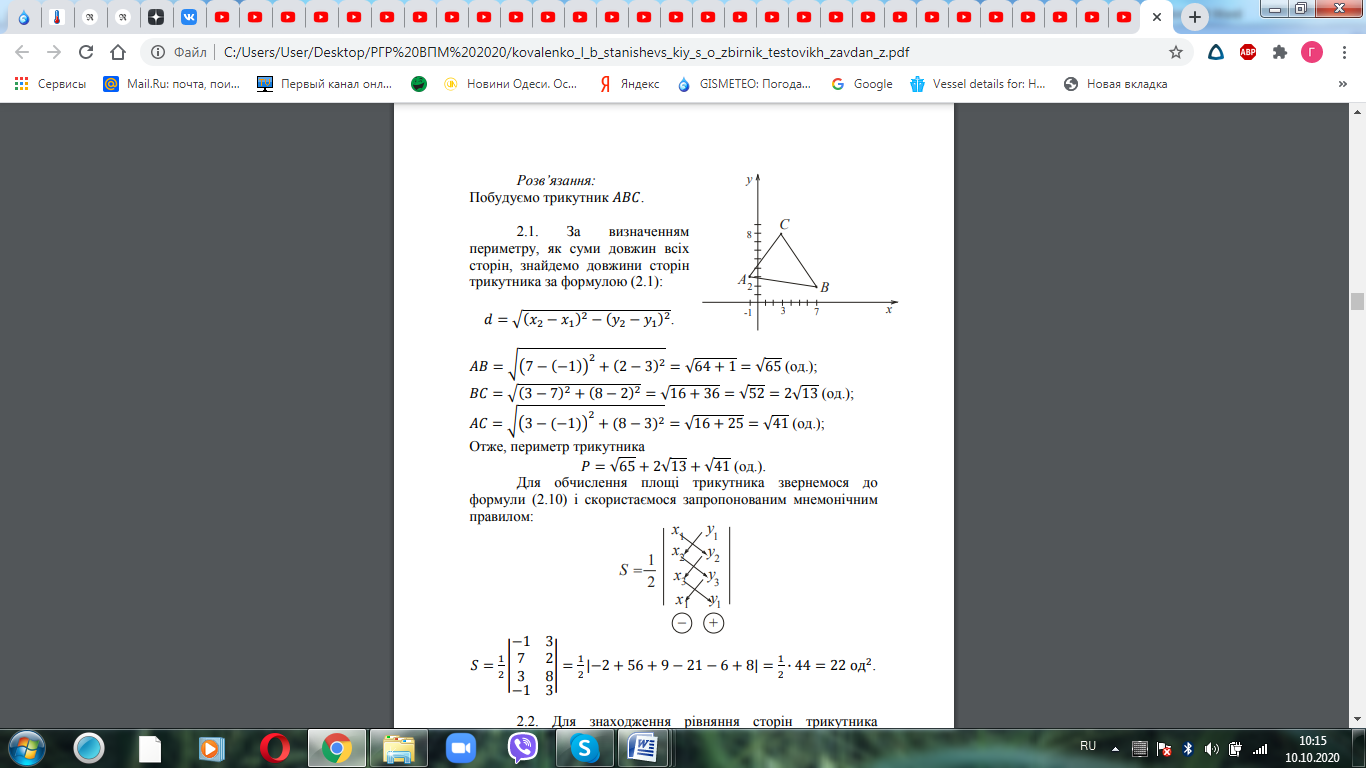
а) Для знаходження рівнянь сторін трикутника скористаємося рівнянням прямої, що проходить через дві точки:

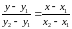
та запишемо отримані рівняння у вигляді рівняння прямої з кутовим коефіцієнтом.

Рівняння прямої :

; ; ;

; ; , ( ).

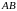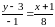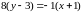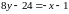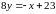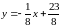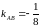Рівняння прямої :

; ; ;

; ; , ( ).

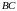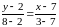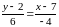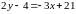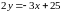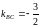Рівняння прямої :

; ; ;

; ; , ( ).

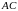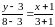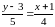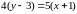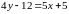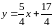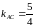Знайдемо довжини сторін трикутника за формулою:

.

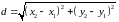Отримаємо:

,

,

.

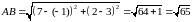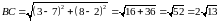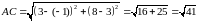б) Кути трикутника знайдемо за формулою:

.

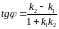Кутові коефіцієнти сторін трикутника:

.

, ;

, ;

, .

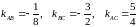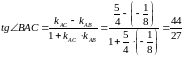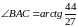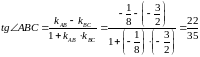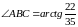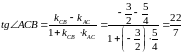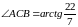в) Визначимо тип трикутника. В п. а) знайдені довжини сторін трикутника 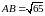, , 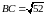, отже, трикутник різносторонній.

З умови 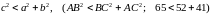прямує, що трикутник гострокутний . Зауважмо, що в згаданій нерівності за вважаємо найдовшу з сторін.

г) За означенням, медіана 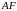поділяє протилежну сторону навпіл. Знайдемо координати точки 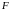як середини відрізка за формулами:

.

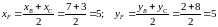Отже, 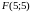. Рівняння прямої :

; ; ;

; ; .

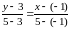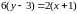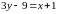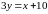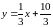д) Висота 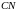перпендикулярна стороні . За умовою перпендикулярності маємо:

.

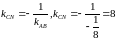Скористаємося рівнянням пучка прямих, що проходять через задану точку С:

.

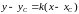Підставляючи в останнє рівняння 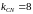та координати точки , отримаємо

.

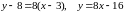Довжина висоти дорівнює відстані від точки С до прямої АВ, яку можна знайти за формулою:

.

Перепишемо рівняння АВ у вигляді загального:

АВ: .

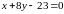Тоді

.

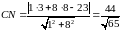е) Периметр трикутника та площа трикутника:

,

.
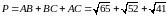
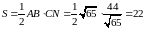