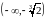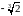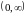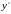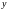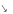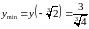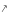Зразок виконання ргр з впм Тема «елементи математичного аналізу» (зад. 8-10)

Задача № 8. За допомогою методів диференціального числення дослідити функцію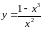 та побудувати її графік.

Розв’язання.

1. Область визначення функції: .

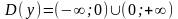2. Дослідимо функцію на парність:

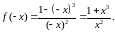
Отже, не виконуються ні рівність 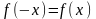, ні , тому дана функція загального вигляду.

3. Знайдемо точки перетину графіка функції з осями координат:

а) в точці 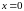функція не визначена, отже крива не перетинає вісь ординат;

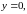
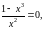
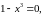
б) 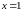. Графік функції перетинає вісь абсцис в точці (1,0);

Оскільки задана функція є елементарною, то вона неперервна на всій області визначення. Отже, залишається дослідити на неперервність точку . Знайдемо односторонні границі в точці :

4. Оскільки задана функція є елементарною, то вона неперервна на всій області визначення. Отже, залишається дослідити на неперервність точку . Знайдемо односторонні границі в точці :

,

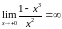отже, в точці функція має розрив 2-го роду.

5. Знайдемо асимптоти.

а) Оскільки точка – точка розриву другого роду, то рівняння вертикальної асимптоти: .

б) Рівняння похилої асимптоти шукаємо у вигляді :

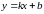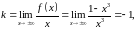
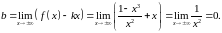
Отже, рівняння 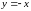– рівняння похилої асимптоти.

6. Щоб визначити інтервали монотонності і точки екстремуму функції 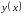, знайдемо першу похідну:

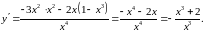
Маєм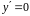о , якщо – стаціонарна точка. У точці 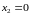функція та її похідна не визначені. Розділяємо область визначення функції на проміжки. Дослідимо знак похідної на кожному проміжку. За знаком першої похідної визначимо проміжки монотонності функції та знайдемо точки екстремуму.

а) На проміжках 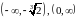, 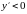– функція спадає;

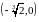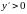б) на , похідна – функція зростає.

в) При переході через точку 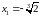похідна змінює знак з мінуса на плюс. Тому в цій точці функція має мінімум:

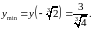
В околі точки 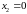похідна змінює знак з плюса на мінус. Проте зробити висновок, що в точці функція має максимум, неможливо, оскільки в цій точці функція не визначена.

Зведемо одержану інформацію в таблицю:

				0
	–	0	+	Не визнач.	–
				Не визнач.

7. Щоб знайти інтервали опуклості та угнутості графіка функції, обчислимо другу похідну:

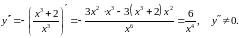
Критична точка другого роду 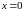. Розбиваємо область існування функції на інтервали: 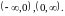Знак другої похідної і інтервали опуклості і угнутості графіка функції зображено на рисунку 1.

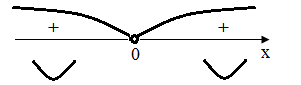
Рис. 1.

Оскільки у точці функція та її похідні не визначені, графік функції немає перегину.

6. За результатами проведеного дослідження побудуємо графік функції.

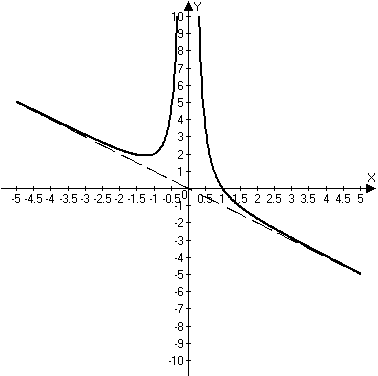
Рис. 2.

Задача № 9. Знайти градієнт функції та похідну функції за напрямком вектора 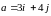у точці .

Розв’язання. За означенням (6.34):

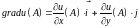
Знайдемо частинні похідні першого порядку:

.

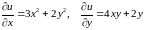Обчислимо їх значення в точці :

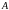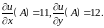
_Тоді

.

Похідна функції 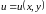за напрямком вектора 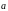за формулою [] дорівнює:

,

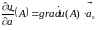де 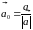– орт вектора .

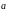Для заданого вектора знаходимо:

.

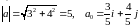Тоді

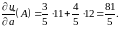
Задача 10. Дослідити функцію 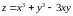на екстремум.

Розв’язання. Задана функція є визначеною і диференційованою для всіх 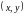, тому її екстремум може бути тільки у стаціонарних точках. Визначимо стаціонарні точки заданої функції, тобто точки підозрілі на екстремум. Для цього знайдемо частинні похідні першого порядку та прирівняємо їх до нуля.

; .

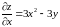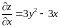В результаті отримаємо:

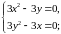
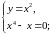
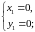
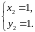
Маємо дві стаціонарні точки: 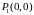, . Для того щоб скористатися достатньою умовою екстремуму, знайдемо частинні похідні другого порядку:

, , .

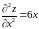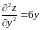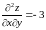Перевіримо достатні умови для точки :

, , .

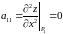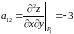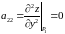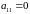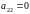Оскільки і , то згідно з умовою [1, стр. 424 ] , екстремуму в точці немає.

Відповідно для точки маємо:

, , ,

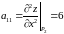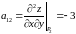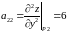тобто

,

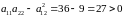Тоді в точці є екстремум і це мінімум:

.

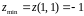а) Дослідити функцію і побудувати її графік.