
Лекція № 4. Елементи АнГеом
.pdf
ТЕМА 3 «ЕЛЕМЕНТИ АНАЛІТИЧНОЇ ГЕОМЕТРІЇ НА ПЛОЩИНІ»
§1. Рівняння прямої на координатній площині.
1.Загальне рівняння прямої.
Розглянемо ненульовий вектор прямої l на координатній площини, і проходить ця пряма (рис. 3.11).
n (A; B)
довільну
, який |
перпендикулярний |
до |
точку |
M0 x0 ; y0 , через |
яку |
Рис. 3.11.
Тоді для будь-якої точки M x; y , яка належить прямій l , можна
вектор M0 M x x0 ; y y0 . Оскільки M0 M l , тоді вектори перпендикулярні. З умови перпендикулярності векторів маємо n M
побудувати
M 0 M |
і n |
0 M 0 |
або |
A x x |
B y |
0 |
|
y |
|
0 |
|
0
.
(3.27)
Це рівняння називають рівнянням прямої, що проходить через задану точку перпендикулярно даному вектору, а вектор n A; B – нормаллю до цієї прямої.
Розкривши дужки у (3.27) та привівши подібні, отримаємо таке рівняння:
Ax By Ax0
Позначивши C Ax0 By0 , отримаємо
координатній площині
By |
0 |
0 |
|
загальне
.
рівняння прямої на
1

Якщо
C
0
Ax By C
, то отримаємо рівняння
0
.
(3.28)
якому задовольняють
Ax By 0
координати т. O 0;0
,
.
(3.29)
Отже, ця пряма проходить через
початок координат. Якщо A 0 та
B
0
, то рівняння прямої набуває вигляду
By C 0
або
|
|
|
|
|
y b , |
(3.30) |
|
де |
b |
C |
. Нормаль |
n 0; B |
цієї прямої перпендикулярна |
||
B |
|||||||
|
|
|
|
|
|
||
пряма |
(3.29) паралельна до Ox . Якщо у рівнянні (3.30) |
b |
y 0 , |
яке є рівнянням осі Ox . |
|
Якщо |
A 0 |
і B 0 |
, то рівняння прямої набуває вигляду |
до осі
0 , то Ax C
Ox , отже
отримаємо
0 |
, або |
де a
пряма x 0 ,
|
C |
. Нормаль |
n |
|
A |
||||
|
|
|
(3.30) паралельна що є рівнянням осі
|
x a , |
(3.31) |
|
A;0 |
цієї прямої перпендикулярна |
||
до Oy . Якщо у рівнянні (3.31) |
a |
||
Oy . |
|
|
|
до осі Oy , тому
0 , то отримаємо
2. Рівняння прямої з кутовим коефіцієнтом.
Нехай у загальному рівнянні прямої рівняння y через x :
B 0
, тоді виразимо з цього
|
|
|
|
|
|
|
|
||
|
|
|
|
|
y kx b , |
(3.32) |
|
|
|
де k |
A |
, b |
C |
|
|
|
|
|
|
. З’ясуємо геометричний зміст коефіцієнтів k |
і b (рис. 3.11), |
||||||||
B |
B |
||||||||
|
|
|
|
|
|
|
|||
вважаючи що ці коефіцієнти додатні. Якщо у рівняння (3.32) підставити x 0 , |
|||||||||||
знайдемо, що y b . |
Отже т. F 0;b належить прямій, а b |
визначає відрізок, |
|||||||||
який відтинається прямою на осі |
Oy |
. Якщо ж у |
(3.32) |
b 0 |
, |
тоді пряма |
|||||
проходить через початок координат. Знайдемо точку |
L перетину цієї прямої з |
||||||||||
віссю Ox . Оскільки координата |
y |
цієї точки дорівнює нулю, то з рівняння |
|||||||||
kx b 0 знайдемо |
координату |
x |
цієї |
очки. Таким |
чином, знайдено точку |
||||||
|
|
b |
|
|
|
|
|
|
|
b |
|
L |
|
|
;0 . Розглянемо LFO O |
|
, у якому OF |
b й |
OL |
|
. Знайдемо |
||
|
|
||||||||||
|
|
k |
|
|
|
2 |
|
|
|
k |
|
тангенс
FLO
:
tg |
OF |
або |
tg k |
(3.33) |
|
OL |
|||||
|
|
|
|
||
|
|
|
|
|
Таким чином, коефіцієнт k дорівнює тангенсу кута між прямою й додатним напрямком вісі Ox і називається кутовим коефіцієнтом. Тому рівняння (3.32) називають рівнянням прямої з кутовим коефіцієнтом.
2

M |
0 |
|
Якщо |
||
x |
; y |
|
0 |
0 |
|
l
для прямої |
l |
відомий кутовий коефіцієнт |
k |
і деяка точка |
, то можна записати ще один вид рівняння з кутовим коефіцієнтом
|
|
y y0 k x x0 , |
(3.34) |
|
|
яке називають рівнянням прямої, що проходить через дану точку у заданому напрямку, або рівнянням пучка прямих.
3. Канонічне та параметричні рівняння прямої.
Будь-яка пряма |
на площині може бути задана |
за |
допомогою точки |
M0 x0 ; y0 , через яку вона проходить, і ненульового вектора |
s m;n , до якого |
||
вона паралельна (рис. |
3.11). Для будь-якої точки M , |
що належить прямій, |
|
вектори s і M 0 M є колінеарними. Тоді з умов колінеарності їх координати пропорційні, тобто, виконується рівність:
|
|
|
|
|
|
|
x x0 |
|
y y0 |
, |
(3.35) |
|
m |
n |
|||
|
|
|
|
Рівняння (3.35) називається канонічним рівнянням прямої на площині.
Вектор |
s , до якого пряма паралельна, називається її напрямним вектором. |
З іншого боку, |
з колінеарності векторів |
s і M 0 M випливає, що існує |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
x x |
|
mt |
|
||
число t R таке, що |
M 0 M t s |
, |
або в координатній формі |
|
0 |
|
. Тоді |
||||||||||
y y |
|
nt |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
отримаємо: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
x mt x |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
0 |
. |
|
(3.36) |
|
|
|
|
|
|
|
|
|
y nt y |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Рівняння (3.36) називаються параметричними рівняннями прямої на |
|||||||||||||||||
площині. Тут також вектор |
s m;n – напрямний вектор |
прямої, |
точка |
||||||||||||||
M0 x0 ; y0 належить цій прямій, а t R – параметр. |
|
|
|
|
|
||||||||||||
Будь-яка пряма однозначно визначається своїми двома точками. Нехай |
|||||||||||||||||
точки M1 x1; y1 і M2 x2 ; y2 належать прямій. |
Тоді в якості вектора s |
можна |
|||||||||||||||
взяти вектор M1M2 x2 |
x1; y2 |
y1; z2 |
z1 , а в якості точки M 0 – |
точку M1 . |
|||||||||||||
Тоді з рівняння (3.35) |
отримаємо рівняння прямої, що проходить через дві |
||||||||||||||||
точки: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
x x1 |
|
y y1 |
, |
(3.37) |
|
|
|
|
|
|
||||
|
|
|
x x |
|
|
|
|
|
|
|
|||||||
|
|
|
|
y |
|
y |
|
|
|
|
|
|
|
||||
|
|
|
|
2 |
1 |
2 |
1 |
|
|
|
|
|
|
|
|
||
3
4. Рівняння прямої у відрізках на осях. |
|
|
||||||||
Нехай пряма не проходить через початок координат і перетинає осі |
||||||||||
координат у точках |
M1 a;0 і M |
2 0;b , тоді з (3.37) отримаємо |
||||||||
|
|
|
|
|
|
x - a |
|
y 0 |
, |
|
|
|
|
|
|
|
0 a |
b 0 |
|||
|
|
|
|
|
|
|
|
|
||
або |
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
y |
1, |
|
|
(3.38) |
|
|
|
|
a |
b |
|
|
|
||||
|
|
|
|
|
|
|
|
|
||
яке називається рівнянням прямої у відрізках на осях.
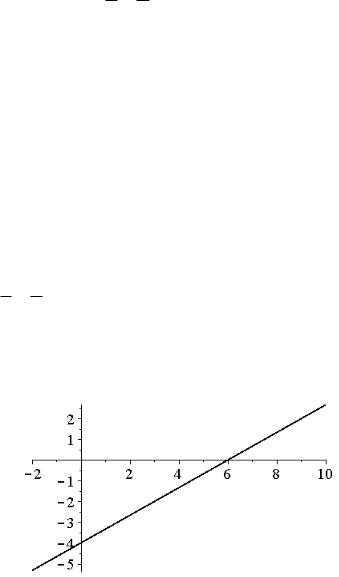
Приклад1. Визначити точки перетину прямої координатними осями та накреслити цю пряму.
Розв’язання.
2x 3y 12 0
з
M |
1 |
|
На осі
(6,0) |
. На |
|
Ox
осі
y 0 Oy
,тому 2x
x0 , тому
12 0,3y
x 6 , 12 0,
і точкою перетину з віссю Ox |
є |
y 4 |
, отже, точкою перетину |
|
прямої з |
Oy |
є |
M |
2 |
(0, 4) |
. Отже, задане рівняння можна записати згідно ( |
3.38) |
у |
|||
|
|
|
|
|
|
||||||
відрізках на осях |
|
x |
|
y |
1. |
||||||
|
6 |
4 |
|||||||||
|
|
|
|
|
|
|
|
|
|
||
Для побудови прямої зобразимо ці точки на координатній площині та проведемо через них пряму:
§ 2. Кут між прямими на координатній площині.
Нехай прямі на координатній площині (рис. 3.12) задані рівняннями з кутовими коефіцієнтами l1 : y k1 x b1 і l2 : y k2 x b2 . Знайдемо кут між
прямими.
4
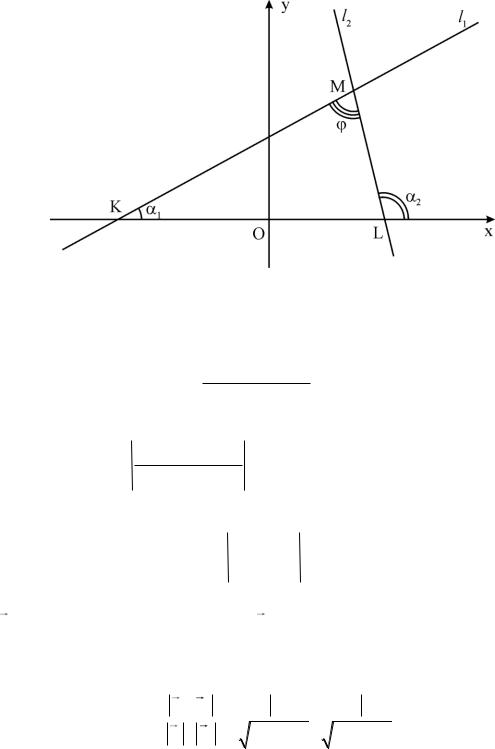
Кутом
між прямими на координатній площині називається найменший
з двох кутів, утворених при перетині цих прямих.
Використовуючи властивість кутів трикутника: зовнішній кут при вершині трикутника дорівнює сумі двох внутрішніх кутів, які не суміжні з цим кутом, з KLM отримаємо таке співвідношення між кутами 1 , 2 і
|
2 |
|
|
1 |
|
або
|
2 |
|
1 |
|
|
Рис. 3.12.
|
|
|
|
|
|
|
Якщо |
2 |
, |
тоді |
|
тригонометрії |
tg tg 2 |
1 |
|||
кутів |
1 і 2 |
більший, |
а |
кут |
|
можемо скористатися відомою формулою
|
tg |
2 |
tg |
|
|
|
|
|
|
|
1 |
|
. |
Оскільки невідомо, який |
з |
||
1 tg |
tg |
|
||||||
|
2 |
|
|
|
||||
|
|
|
1 |
|
|
|
|
|
|
між |
|
прямими |
|
завжди гострий, отже tg |
є |
||
додатнім. Значить |
tg |
tg |
2 |
tg |
1 |
. Враховуючи, |
що k1 tg 1 |
||||||
|
|
||||||||||||
tg tg |
|||||||||||||
|
1 |
2 |
|
|
|
|
|
||||||
|
|
|
|
1 |
|
|
|
|
|
|
|
||
отримаємо формулу для визначення кута між прямими |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
tg |
|
|
k2 k1 |
|
|
(3.40) |
|
||
|
|
|
|
1 k |
k |
|
|
|
|||||
|
|
|
|
|
|
|
1 |
|
2 |
|
|
|
|
і
k |
2 |
|
|
|
tg |
2 |
|
,
Якщо для прямих на координатній площині простіше визначити напрямні вектори si mi ;ni , i 1,2 або нормалі ni Ai ; Bi , i 1,2 , то для визначення
кута між цими прямими можна використовувати формули для визначення кута між векторами, які набувають вигляду:
cos |
s1 |
s2 |
|
|
|
m1m2 n1n2 |
|
|
(3.41) |
||
s1 |
s2 |
|
|
|
|
|
|
|
|||
|
|
|
m2 |
n2 |
m2 |
n2 |
|||||
|
|
|
1 |
1 |
2 |
2 |
|
|
|||
5

і |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos |
n |
|
n |
|
|
|
|
|
|
A A B B |
|
|
|
|
. |
(3.42) |
|
|||||||||||||
|
|
|
|
1 |
2 |
|
|
|
|
|
1 |
2 |
|
|
|
1 |
|
2 |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
n |
|
n |
|
|
|
2 |
|
B |
2 |
|
A |
2 |
B |
2 |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
1 |
|
2 |
|
|
|
|
A |
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
1 |
|
|
|
|
2 |
2 |
|
|
|
|
|
||||||||
Якщо прямі l1 і l2 паралельні, то кут |
та напрямні вектори |
і нормалі |
||||||||||||||||||||||||||||||||
паралельні. Отже, отримаємо такі умови паралельності прямих |
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
k1 k2 |
|
або |
|
|
m1 |
|
n1 |
або |
|
A1 |
|
|
|
B1 |
|
|
(3.43) |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
m2 |
|
|
A2 |
|
|
B2 |
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
n2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Якщо ж прямі перпендикулярні, |
то кут |
|
, при якому tg |
не існує, а |
||||||||||||||||||||||||||||||
2 |
||||||||||||||||||||||||||||||||||
cos 0 . |
|
|
|
|
|
|
tg |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
З ( |
3.40 |
) маємо, що |
не існує, |
якщо знаменник правої частини |
||||||||||||||||||||||||||||||
дорівнює |
нулю 1 |
k1 k2 0 |
, а з ( |
3.41 |
) і ( |
3.42 |
) отримуємо, |
що |
чисельники |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
правих частин дорівнює нулю. Таким чином, маємо умови перпендикулярності прямих
|
k2 |
1 |
або |
s1 s2 0 |
або n1 n2 0 |
(3.44) |
|
|
|
|
k |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
Приклад. Написати рівняння прямої, що проходить через точку |
A 1;2 |
||||||||
перпендикулярно до прямої, яка проходить через точки |
M1 |
2;4 і M2 |
5;1 . |
||||||
Розв’язання.
З (3.37) запишемо рівняння прямої, що проходить через дві точки
|
|
|
|
x 2 |
|
y 4 |
або |
x 2 |
|
y 4 |
. |
|
|
|
|||||||||||||||||||
|
|
|
|
5 2 |
1 |
4 |
|
7 |
|
|
|
|
3 |
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
Приведемо це рівняння до рівняння з кутовим коефіцієнтом, для цього |
|||||||||||||||||||||||||||||||||
виразимо з нього |
y через x |
. Маємо |
|
y |
3 |
x |
10 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
7 |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
З останнього рівняння |
визначимо |
кутовий |
|
|
коефіцієнт |
k1 |
3 |
. |
|||||||||||||||||||||||||
|
|
7 |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Використовуючи |
умову |
перпендикулярності |
|
( |
3.44 |
), |
|
|
знайдемо |
кутовий |
|||||||||||||||||||||||
коефіцієнт шуканої прямої |
k |
|
|
1 |
|
7 |
. |
Знаючи точку, |
через яку проходить |
||||||||||||||||||||||||
2 |
k |
|
3 |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
пряма та її кутовий коефіцієнт, з ( |
3.34 |
) визначимо рівняння шуканої прямої |
|
|
|||||||||||||||||||||||||||||
|
y |
2 |
7 |
|
x 1 |
|
|
|
y |
7 |
x |
13 |
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
або |
|
|
|
|
. |
|
|
|
|
|
|||||||||||||||||||
|
3 |
|
|
3 |
3 |
|
|
|
|
|
|||||||||||||||||||||||
6

§ 3. Відстань від точки до прямої на координатній площині.
Нехай пряма l задана загальним |
рівнянням |
Ax By C 0 . Знайдемо |
|||||||||||||
відстань від точки M |
0 x0 |
; y0 до прямої l |
|
(рис. 3.13). |
|
|
|
|
|
|
|
||||
Відстань від т. |
M 0 |
до прямої l |
дорівнює модулю проекції вектора M1M 0 |
||||||||||||
на нормаль n A; B , де |
M1 x1; y1 довільна точка, яка належить прямій |
l : |
|||||||||||||
|
|
|
n M |
M |
|
|
Ax By |
|
Ax By |
|
|
||||
d прn M1M0 |
0 |
|
0 |
0 |
|
1 |
1 |
|
|
||||||
|
1 |
|
|
|
|
|
|
|
. |
|
|||||
|
n |
|
|
|
A |
B |
2 |
|
|
||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
Рис. 3.13. |
|
Оскільки т. M1 l , отже |
Ax1 By1 C 0 |
або C Ax1 By1 . Тому |
маємо формулу для відстані від точки до прямої:
d
Ax |
By |
0 |
|
|||
0 |
A |
|
|
|
|
|
|
2 |
B |
2 |
|||
|
|
|
|
|
||
C
 .
.
(3.45)
7
