Якщо функція має скінченну границю в точці
x0
, то вона обмежена в
деякому околі цієї точки. |
|
Границя сталої величини дорівнює цій сталій: |
lim c c, c const . |
|
x x |
|
0 |
Нехай функція |
y f x визначена на множині всіх дійсних чисел. |
|
Означення. Число |
||
якщо |
M M |
||
виконується нерівність |
|
f |
|
|
|
|
1 |
|
Наприклад, lim |
|
|
|
x |
x |
|
|
|
|
|
A називається границею функції |
y f x при |
|||
0 |
таке, що |
x , для якого |
виконується |
|
x A . Записується це так: lim f x A . |
||||
|
|
|
|
x |
|
|
x |
|
|
1 1, lim e |
0 . |
|
||
|
|
|||
|
x |
|
|
|
|
|
|
|
|
x 
x
M
,
,
Також важливим у математичному аналізі є поняття про односторонні границі.
|
Означення. Число |
|
називається границею функції y f x у точці x0 |
||||||||||
|
A |
||||||||||||
зліва, якщо |
|
0 |
таке, що x x0 |
x0 |
виконується |
||||||||
нерівність: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f x |
|
(1.3) |
|
|
|
|
|
|
|
|
|
|
|
A . |
|
|
|
|
||
|
Аналогічно, число |
|
називається границею функції y f x |
у точці |
|||||||||
|
A |
|
|||||||||||
x0 справа, якщо |
|
0 таке, що |
x x0 ; x0 виконується |
||||||||||
нерівність: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1.4) |
|
|
|
|
|
|
|
|
|
|
|
f x A . |
|
|
|
|
||
|
Скорочено |
границя |
|
зліва |
записується |
так: |
lim |
f x A |
|
або |
|||
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
x x 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
f (x0 |
|
, а |
границя |
|
справа |
відповідно так: |
lim |
|
|
або |
|||
0) A |
|
f x A |
|||||||||||
|
|
|
|
|
|
|
|
|
|
x x0 0 |
|
|
|
f (x |
0) A |
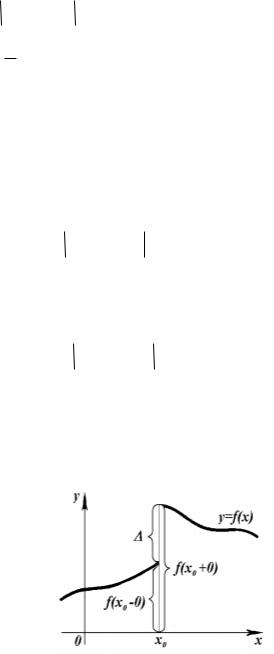
(рис. 1.2). |
|
|
|
|
|
|
|
|
|
||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 1.2
4. Основні властивості функцій, що мають границю.
Нехай задано дві функції u u x |
і v v x , які мають у точці x0 |
скінченні границі A і B відповідно, тобто |
|
5
lim u x A, x x0
1. Границя суми (різниці) функцій
lim v
x x0 u x
x і v
Bx
.
дорівнює сумі (різниці) їх
границь
lim u x v x
x x0
2. Границя від добутку функцій
lim
x x0 u x
u x
|
і |
v |
x
lim v x
x x0
дорівнює добутку границь
від функцій-множників |
u x v x lim u x lim v x . |
||
lim |
|||
x x |
|
x x |
x x |
0 |
|
0 |
0 |
Наслідок. Сталий множник можна виносити за знак границі |
|||
|
lim c u x c lim u x . |
||
|
x x |
|
x x |
|
0 |
|
0 |
Зауваження. Властивості 1 і 2 справджуються для скінченного числа |
|||
функцій. |
|
u x і |
v x дорівнює частці границь цих |
3. Границя від частки функцій |
|||
функцій за умови, що границя знаменника не дорівнює нулю
4. Функція
lim x x0
y f x
u x |
|
lim u x |
lim v |
|
x x |
||
v x |
0 |
||
|
lim v x |
0 |
|
|
|
|
x x |
|
|
x x |
|
|
|
0 |
|
має границю у точці
x x0
0 |
|
. |
|
тоді та лише тоді, коли
існують обидві її однобічні границі |
|
|
і |
|
у цій |
точці та їх значення |
|||
|
A |
A |
|||||||
дорівнюють між собою. |
|
|
|
|
|
|
|
|
|
lim f x A lim |
f x |
lim |
f |
x A , |
( f (x0 |
0) f (x0 0) A ). |
|||
x x |
x x 0 |
|
x x |
0 |
|
|
|
|
|
0 |
0 |
|
0 |
|
|
|
|
|
|
При обчисленні границі необхідно у першу чергу спробувати підставити граничне значення x0 у функцію під знаком границі. Якщо при цьому
одержимо число А, то це число і є границею.
Приклад. Обчислити lim |
2x |
3 |
x |
2 |
5 . |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
x 2 |
|
|
|
|
|
|
|
|
|
|
|
|
Розв’язання. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim |
2x3 x2 |
5 |
|
lim 2x3 |
lim x2 lim5 2 |
lim x |
3 |
lim x |
2 |
5 |
||||||
x 2 |
|
|
x 2 |
|
|
x 2 |
|
x 2 |
x 2 |
|
x 2 |
|
|
|||
2 8 4 5 17 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
5. Нескінченно великі та нескінченно малі функції. |
||||||||||||||||
Нехай функція |
y f x |
визначена |
в деякому околі точки |
|
x0 , крім, |
|||||||||||
можливо самої точки x0 .
6
x 0
|
|
|
Означення. Функція |
y f x |
називається нескінченно великою при |
|||
x0 |
, якщо |
M 0 M 0 |
таке, що x , яке вдовольняє нерівності |
|||||
|
|
x x0 |
|
|
, виконується нерівність |
f x M . |
||
|
|
|||||||
|
|
|
Це записується так: |
lim f x . |
||||
|
|
|
|
|
|
|
x x0 |
|
|
|
|
1 |
|
|
|
|
Наприклад, |
функція y |
|
є нескінченно великою у точці |
x0 |
|||
x 4 |
|||||||
оскільки lim |
1 |
|
. |
|
|
|
|
|
|
|
|
|
|||
x 4 |
|
|
|
||||
x 4 |
|
|
|
|
|
||
Аналогічно означаються границі lim f x та |
lim f x |
||||||
|
|
|
|
|
x x0 0 |
x x0 0 |
|
.
4
,
Наприклад, lim |
1 |
, |
lim |
1 |
. |
|
|
|
|
||||
x 0 0 |
x |
x 0 0 |
x |
|
||
Функція може бути нескінченно великою при |
||||||
записується так: lim f x . Наприклад, lim x2 |
. |
|||||
x |
|
|
|
|
x |
|
x
,
тоді це
|
Означення. Функція |
y |
|||
x x0 |
, якщо |
lim f x 0 . |
|
|
|
|
|
x x |
|
|
|
|
|
0 |
|
|
|
|
Функція |
y f x |
може |
||
lim f x 0 . |
|
|
|
|
|
x |
|
|
|
|
|
f x
бути
називається нескінченно
нескінченно малою при
малою
x ,
при
тоді
Наприклад,
що |
lim(x 2) |
3 |
0 |
, |
|
|
|||||
|
x 2 |
|
|
|
|
lim |
1 |
0 . |
|
|
|
|
|
|
|
||
x x |
|
|
|
|
|
Відмітимо нескінченно малих
функція y (x 2)3 є нескінченно малою при |
x 2 , тому |
||||
а функція y |
1 |
є нескінченно малою при |
x , тому що |
||
x |
|||||
|
|
|
|
||
декілька основних властивостей нескінченно великих і функцій.
1.Сума скінченого числа нескінченно малих функцій у т. x0 є
нескінченно мала функція у цій точці.
2.Сума скінченого числа нескінченно великих функцій одного знаку у т. x0 є нескінченно велика функція того ж знаку у цій точці.
3.Добуток двох нескінченно малих (великих) функцій у т. x0 є
нескінченно мала (великих) функція у цій точці.
4.Добуток нескінченно малої (великої) функції у т. x0 на функцію,
обмежену у т. |
x |
|
|
|
x |
0 . |
|
0 , є нескінченно малою (великою) функцією у т. |
|
||||||
5. Якщо функція x – нескінченно мала у т. x0 |
і x |
0 в деякому |
|||||
проколотому околі цієї точки, то функція |
1 |
є нескінченно великою у т. x0 , |
|||||
|
|||||||
x |
|||||||
|
|
|
|
|
|
||
7
та навпаки, якщо функція |
x |
|
– нескінченно велика у т. x0 , тоді |
1 |
є |
|||||||||
|
x |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
нескінченно малою у т. |
x0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
Перераховані властивості легко запам’ятати, якщо використовувати |
||||||||||||||
символічний запис, зв’язавши з |
нескінченно малою функцією символ «0», з |
|||||||||||||
нескінченно великою функцією – символ « |
» а з обмеженою функцією – |
|||||||||||||
символ «С»: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 0 0, |
0 0 0, |
0 C 0, |
|
|
||||||||||
, |
, |
C , |
|
|
||||||||||
|
|
1 |
, |
|
1 |
0 . |
|
|
|
|
|
|||
|
|
0 |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Два останні співвідношення між нескінченно малими та нескінченно |
||||||||||||||
великими функціями часто використовуються при обчисленні границь. |
|
|
||||||||||||
|
x2 3x 2 |
|
|
02 3 0 2 |
|
|
2 |
|
|
|||||
Наприклад, lim |
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
x 0 |
|
tgx |
|
|
tg0 |
|
|
|
0 |
|
|
|||
Нагадаємо, що 0 у виразі в дужках – це символ нескінченно малої функції.
6.Приклади обчислення границь. Поняття про невизначеності.
Розглянемо приклади функцій.
Приклад 1. Обчислити
обчислення
|
x |
2 |
5x 3 |
||
|
|
|
|||
lim |
x |
2 |
x 2 |
||
x 1 |
|||||
|
|||||
границь дробово-раціональних
.
Розв’язання. |
|
|
|
Підставимо у дріб граничне значення |
x0 |
1 |
, тоді за властивістю границі |
частки отримаємо: |
|
|
|
|
x |
2 |
5x 3 |
|
1 5 3 |
3 |
|
|
|
|
|
|
|
||
lim |
x |
2 |
x 2 |
|
1 1 2 |
. |
|
x 1 |
|
2 |
|||||
|
|
||||||
Приклад 2. Обчислити lim |
2x2 |
5x 3 |
. |
|
|
x2 |
9x 8 |
|
|
||
x 1 |
|
|
|||
Розв’язання. |
|
|
|
|
|
Застосувати в цьому випадку теорему про границю частки не можна, |
|||||
оскільки границя знаменника дорівнює 0 коли |
x 1. Окрім того, границя |
||||
чисельника також дорівнює 0. У таких випадках кажуть про невизначеність
0
виду . Для її розкриття розкладемо чисельник і знаменник на множники, а
0
потім скоротимо спільний множник чисельника та знаменника.
8
|
2x |
|
5x 3 |
|
0 |
|
|
|
|
|
2x 3 |
|
|
2x 3 |
|
2 3 |
1 |
|||||
lim |
|
|
2 |
|
|
|
|
|
lim |
|
x 1 |
|
lim |
|
|
|
|
. |
||||
|
2 |
9x 8 |
|
|
|
|
|
x 8 |
|
x 8 |
1 8 |
|||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||
|
x |
|
|
|
|
0 |
|
|
|
|
7 |
|||||||||||
x 1 |
|
|
|
|
|
|
|
|
x 1 |
|
|
|
|
|
|
|
x 1 |
|
|
|
|
|
Отже, якщо границя |
|
відношення |
двох |
|
|
многочленів |
|
при |
x x0 |
|||||||||||||
є
невизначеністю виду |
|
0 |
|
, то для її розкриття потрібно чисельник і знаменник |
|||||||||||||||||
|
0 |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
розкласти на множники, серед яких обов’язково буде |
|
множник ( x x0 ), |
|||||||||||||||||||
скоротити дріб на нього та перейти до границі при |
x x0 |
. В деяких випадках |
|||||||||||||||||||
треба поділити чисельник і знаменник на двочлен |
x x0 , |
а потім перейти до |
|||||||||||||||||||
границі при x x0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Якщо |
|
границя |
|
|
відношення |
|
двох |
|
многочленів |
при x є |
|||||||||||
невизначеністю виду |
|
|
, то для її розкриття потрібно поділити чисельник і |
||||||||||||||||||
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
знаменник на |
x |
k |
, де k |
– найбільший степінь |
x |
усього дробу. |
|
||||||||||||||
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
3x |
3 |
7x 120 |
|
|
|
|
|
|||||
Приклад 3. Обчислити lim |
|
. |
|
|
|
|
|||||||||||||||
|
5 |
2x |
3 |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Розв’язання. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
У цій границі маємо невизначеність |
|
при x |
. Для її розкриття |
||||||||||||||||||
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
поділимо чисельник і знаменник на |
x |
3 |
: |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
3 |
7 |
|
120 |
|
|
|
|
|
7 |
|
120 |
|
||||||||||||
|
3x |
3 |
7x |
120 |
|
|
|
|
x |
|
x |
|
|
|
lim 3 |
x |
2 |
|
x |
3 |
|
|||||||||||||||
lim |
|
|
lim |
|
|
|
|
2 |
|
3 |
|
x |
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
5 2x |
3 |
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
x |
|
|
|
|
|
|
|
x |
|
|
|
|
2 |
|
|
|
lim |
2 |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
3 |
|
|
|
|
3 |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
x |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
оскільки при |
x |
кожен з дробів |
7 |
|
, |
120 |
, |
5 |
|
прямує до нуля. |
|
|
|
|||||||||||||||||||||||
x2 |
|
|
x3 |
x3 |
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Отже, границя відношення двох многочленів при |
|
x : |
|
|
|
|
||||||||||||||||||||||||||||||
3
2
,
Крім розглянутих невизначеностей |
0 |
|
та |
|
|
існують ще наступні: |
||||||
|
|
|
|
|
||||||||
|
||||||||||||
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
0 |
|
|
0 |
. Розкриття невизначеності в цих випадках може |
|||||||
0 , , 0 |
|
, 1 |
, |
|
||||||||
бути здійснено шляхом тотожних перетворень функції, від якої знаходиться границя, а також за допомогою так званих важливих границь.
9