
- •Лекція № 5. ЕЛЕМЕНТИ МАТЕМАТИЧНОГО АНАЛІЗУ
- •3. Границя функції.
- •4. Основні властивості функцій, що мають границю.
- •5. Нескінченно великі та нескінченно малі функції.
- •7. Неперервність функцій. Класифікація точок розриву.
- •§ 2. Елементи диференціального числення
- •1. Означення похідної . Геометричний
- •та економічний зміст похідної.
- •2. Правила диференціювання.
- •3. Таблиця похідних функцій однієї змінної.

ЛЕКЦІЯ № 5. ЕЛЕМЕНТИ МАТЕМАТИЧНОГО АНАЛІЗУ
§1. Вступ до математичного аналізу.
1.Поняття функції однієї змінної. Способи завдання та
|
|
властивості функцій |
|
|||
Нехай задано дві непусті множини X і Y . |
|
|||||
Означення. Відповідність f , |
яка кожному елементу x X |
ставить у |
||||
відповідність один |
та |
лише |
один |
елемент |
y Y , називається |
функцією і |
записується y f x . |
|
|
|
|
|
|
Якщо множини |
X ,Y є підмножинами множини дійсних чисел , тоді |
|||||
f x – числова |
функція. |
Функцію можна задати різними |
способами: |
|||
аналітичним, графічним або табличним. Коли функція задається аналітично, то відрізняють такі види її завдання: y f x – явне завдання функції, F x, y 0
– неявне завдання,
x x t |
, t I |
|
|
y y t |
|
|
|
|
|
|
|
– параметричне завдання, у якому
t
називають параметром. Якщо функція задається у вигляді графіку, то кажуть про графічний спосіб завдання функції. Якщо ж функція задається за
допомогою таблиці, то маємо табличне завдання функції. |
|
Множина X , для кожного елементу якої визначене значення функції, |
|
називається областю визначення функції і позначається D |
f , а множина всіх |
можливих значень функції називається областю значень функції та |
||||||||
позначається E f . |
|
|
|
|
|
|
||
Означення. Функція y f x |
називається парною, якщо для будь-якого |
|||||||
значення |
x D f , значення x також належить D f і f x f |
x . |
|
|||||
Графік парної функції симетричний відносно осі Oy . |
|
|
|
|||||
Означення. Функція y f x |
називається непарною, якщо для будь- |
|||||||
якого значення x D f , значення x також належить D f і |
f x f x . |
|||||||
Графік непарної функції симетричний відносно початку координат. |
||||||||
Означення. Якщо для будь-яких x1 , x2 D1 D f з нерівності |
x1 x2 |
|||||||
випливає |
нерівність |
f x1 f x2 |
( f x1 f x2 ), |
тоді |
функцію |
f x |
||
називають зростаючою (спадною) на множині D1 . На рис. 1.1 |
зображено |
|||||||
графіки зростаючої (а) та спадної (б) функцій. |
|
|
|
|
||||
Означення. Якщо ж замість строгих нерівностей маємо нестрогі, тобто |
||||||||
f x1 f x2 |
або |
f x1 f x2 , |
тоді функцію |
називають |
відповідно |
|||
незростаючою або неспадною відповідно.
Усі функції, для яких виконуються зазначені вище нерівності, як строгі, так і нестрогі, називають монотонними функціями.
1

|
|
|
|
|
|
|
|
а) |
|
|
|
|
|
(б) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 1.1 |
|
|
|
|
|
|
|
|
||
|
|
|
Означення. Функція |
f x називається обмеженою на множині D , якщо |
||||||||||||||||||
існує таке число |
M 0, |
що |
для |
будь-якого x D |
|
виконується |
нерівність |
|||||||||||||||
|
f x |
|
M . |
|
|
|
|
y sin x |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
Наприклад, |
функція |
обмежена на всій області визначення, тому |
|||||||||||||||||
що sin x 1 |
x R ( M 1). |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
Означення. |
Функція |
f |
x |
з |
областю визначення |
D |
називається |
||||||||||||
періодичною, якщо існує таке число |
T 0 , що для будь-якого x D |
і x kT |
||||||||||||||||||||
також належить D при всіх |
k |
і виконується |
рівність |
f x f x kT . |
||||||||||||||||||
Число T |
називають періодом функції. |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
Нехай |
задана функція |
y f |
x |
з областю |
|
визначення |
D |
і областю |
|||||||||||
значень |
E . |
Якщо будь-якому |
y E |
відповідає |
єдиний |
x D , |
такий що |
|||||||||||||||
|
y f x , тоді кажуть, |
що визначена функція |
x g y |
|
з областю визначення E |
|||||||||||||||||
і областю значень |
D . Таку функцію |
x g y |
називають оберненою до функції |
|||||||||||||||||||
|
y f x і в загальному випадку записують так: x f |
1 |
y . |
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
Наприклад, |
для функції |
y ln x D( y) 0; , E( y) R |
оберненою є |
||||||||||||||||
функція |
x e |
y |
D(x) R, E(x) |
0; . |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Нехай функція |
y f u |
визначена на множині D |
і функція u g x |
||||||||||||||||
визначена на множині |
D1 , |
причому для будь-якого |
|
x D1 |
маємо |
u g x D , |
||||||||||||||||
тоді на множині D1 визначена функція |
y f g x , |
яку називають складною |
||||||||||||||||||||
функцією від |
x |
або композицією функцій y f u |
і |
u g x . Змінну u g x |
||||||||||||||||||
називають проміжним аргументом.
Наприклад, функція
вигляді: |
y ln u , де u |
x . |
y ln |
x |
– складна функція, яку можна подати у |
|
|
D( y) 0; .
2. Елементарні функції та їх класифікація
Серед усіх можливих функцій виділяють так звані основні елементарні функції, до яких належать такі функції:
2

|
|
|
; x |
|
, якщо 0 і є цілим числом, |
|||||||
степенева y x , |
||||||||||||
|
|
|
x ;0 |
0; , якщо |
0, |
|||||||
|
|
|
x 0; |
, при інших 0, |
|
|||||||
|
|
|
x 0; |
, при інших 0 |
; |
|
||||||
показникова y a |
x |
, a |
0, a 0, x |
; |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
||||||
логарифмічна y loga x, a 0, a 1, x 0; ; |
|
|
|
|||||||||
тригонометричні y sin x, |
y cos x, x |
|
, |
|
|
|
||||||
|
y tg x, |
y sec x , |
x |
|
|
k, k |
, |
|
|
|||
|
|
2 |
|
|
||||||||
|
y ctg x, y cosec x , |
|
|
|
|
|
||||||
|
x k, k |
; |
||||||||||
|
|
|
|
y arcsin x, |
y arccos x , |
|
|
|
||||
обернені тригонометричні |
x |
1;1 , |
||||||||||
|
|
|
|
y arctg x, y arcctg x, x . |
||||||||
,
Функція, яка утворена з основних елементарних функцій виконанням скінченого числа арифметичних дій і операцій утворення складної функції,
називається елементарною. Наприклад
y 3sin |
1 |
|
x |
||
|
5ln |
2 |
|

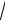 x
x
.
В математиці прийнята наступна класифікація елементарних функцій.
1. Многочлени, або цілі раціональні функції.
Многочленом (цілою раціональною функцією)
n
-го
степеня (
n N
)
називається |
функція вигляду |
Pn (x) a0 x |
n |
a1x |
n 1 |
... an 1x an , де числа |
||||
|
|
|||||||||
a0 , a1 ,..., an R називають коефіцієнтами, a0 |
|
0 |
старшим коефіцієнтом. |
|||||||
Якщо |
n 0, P0 (x) a0 стала величина і |
вважається многочленом 0 |
||||||||
степеня. |
|
|
|
|
|
|
|
|
|
|
2. Дробово-раціональні функції або раціональні дроби. |
||||||||||
Дробово-раціональною функцією називається функція, яка є |
||||||||||
відношенням двох многочленів степенів m і n відповідно: |
||||||||||
|
|
R(x) |
P |
(x) |
|
|
|
|
||
|
|
|
m |
|
. |
|
|
|
||
|
|
Q |
(x) |
|
|
|
||||
|
|
|
|
|
|
|
||||
|
|
|
|
|
n |
|
|
|
|
|
Усі цілі та дробово-раціональні функції утворюють клас раціональних функцій.
3. Ірраціональні функції.
Функції, у яких крім операцій додавання, множення, ділення, піднесення у цілий степінь, присутні операції піднесення у степінь з дробовим (раціональним) показником, називаються ірраціональними функціями. Прикладом такої функції є
f (x) k Pm (x) . Qn (x)
3

Усі раціональні і ірраціональні функції утворюють множину алгебраїчних функцій.
4. Функції, які не є алгебраїчними, називаються трансцендентними. З простіших елементарних функцій до трансцендентних відносяться степеневі з ірраціональним показником степеня, показникові, логарифмічні, прямі і обернені тригонометричні функції.
3. Границя функції.
При формулюванні теорем, а також у визначеннях в математиці часто повторюються окремі вирази і слова. Для їх скороченого запису зручно використовувати спеціальні символи математичної логіки, які називаються кванторами. Розглянемо найбільш поширені з них.
Для скороченого запису окремих виразів в математиці зручно використовувати спеціальні символи математичної логіки, які називаються
кванторами.
– квантор загальності (для будь-якого, для всіх, для кожного). Так наприклад, те, що квадрат будь-якого дійсного числа – невід’ємне число, записується так:
|
|
|
|
x R |
x |
2 |
0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
– квантор існування (існує хоча б один, знайдеться і т.д.). Те, що |
|||||||||||
рівняння |
sin x 1 |
має |
хоча б один дійсний розв’язок, |
можна |
записати |
|||||||
наступним чином: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x R :sin x 1. |
|
|
|
|
|
|||
Нехай функція |
y f x визначена |
в деякому околі точки |
x0 , |
крім, |
||||||||
можливо, самої точки |
x0 . |
|
|
|
|
f x у точці |
|
|
||||
Означення. Число |
A називається границею функції |
x0 |
(або |
|||||||||
при x x0 ), якщо |
(як завгодно малого) |
0 |
таке, що |
x , яке |
||||||||
задовольняє нерівність |
|
|
|
|
0 x x0 |
, |
(1.1) |
виконується нерівність |
|
|
|
|
f x A . |
(1.2) |
|
Скорочено це записують так: lim f x A . |
|||
|
x x |
|
|
|
0 |
|
|
Наприклад, |
lim x2 4. |
|
|
|
x 2 |
|
|
Сенс означення границі функції f x |
у точці x0 полягає в тому, що для |
||
всіх значень x , |
достатньо близьких |
до |
x0 , значення функції f x за |
абсолютною величиною як завгодно мало відрізняються від числа A. Відмітимо очевидні властивості границі функції.
4
