3.Работа и разность потенциалов.

Задача 5. Электрон переместился в ускоряющем поле из точки с потенциалом 200В в точку с потенциалом 300В. Найти кинетическую энергию электрона, изменение потенциальной энергии взаимодействия с полем и приобретенную скорость. Начальная скорость электрона равна нулю.

РЕШЕНИЕ

При перемещении электрона с зарядом е силами электростатического поля совершается работа:

A = -e (φ₁ – φ_2).

Эта работа численно равна изменению потенциальной энергии заряда в электрическом поле, взятому с противоположным знаком:

A = -ΔW_p или ΔW_p = e (φ₁ – φ₂)_.

По теореме о кинетической энергии работа сил электрического поля численно равна приобретенной электроном кинетической энергии W_K:

A = W_K или - e (φ₁ – φ₂) =.

Отсюда скорость электрона, прошедшего разность потенциалов φ₁ – φ_2:



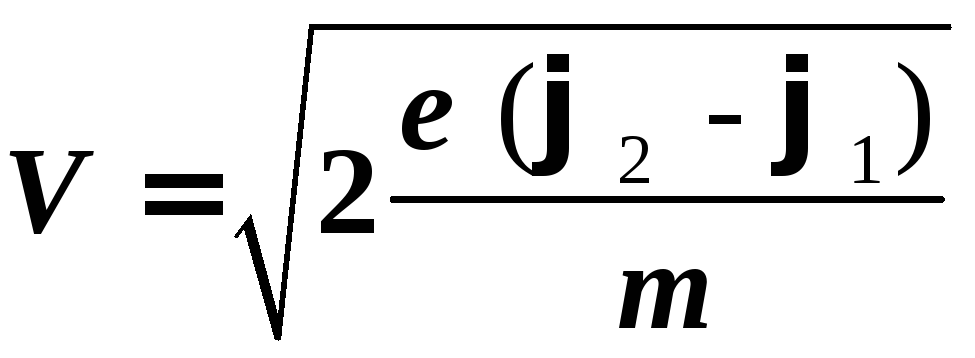
где е = 1,610^-19 Кл, m = 9,110^-31кг — заряд и масса электрона.

Вычисления: W_Р = -1,610^-19 (300 - 200) = -1,610^-17 Дж.

Потенциальная энергия электрона уменьшилась.

W_K = 1,610^-17 Дж.

Кинетическая энергия электрона увеличилась.

.

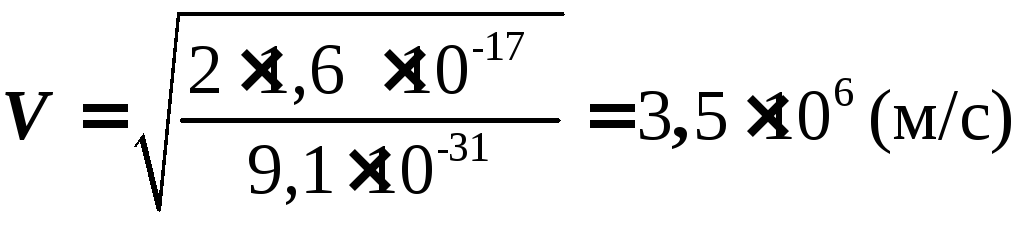4.Движенне заряженных частиц в электростатическом поле

Задача 6. Какова максимальная сила взаимодействия между двумя про­тонами, каждый с энергией 10⁶ эВ, летящих во встречных пучках?

РЕШЕНИЕ

Выберем систему отсчета связанную с одним из протонов, тогда скорость второго протона увеличиться в два раза, а его кинетическая энергия — в четыре раза.По мере сближения протонов кинетическая энергия движущегося протона уменьшается, переходя в потенциальную энергию W_P взаимодействия двух протонов. Условие остановки протонов:

W_К = W_P.

Учитывая, что Wp = q φ получаем:

W_К = q φ (1)

где q — заряд движущегося протона и

(2)

— потенциал поля неподвижного протона, r — расстояние между протонами. Из формул (1-2) находим расстояние r, на которое сблизятся протоны:

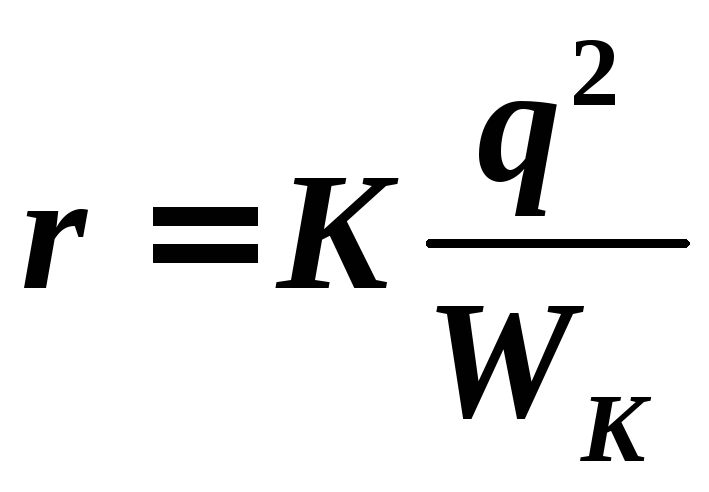. (3)

Зная расстояние r , найдем максимальную силу F взаимодействия протонов. По закону Кулона:

С учетом (3): .

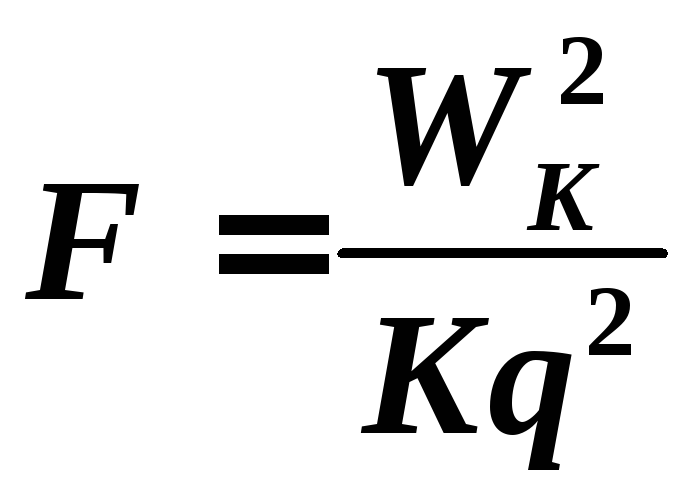Проверка размерности: .

q = 1,610^-19 Кл,

W_K = 410 ⁶ 1,610^-19 = 6,410^-13 Дж.

.

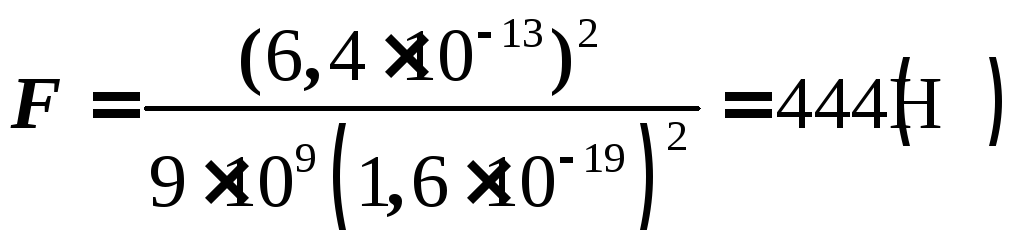Задача 7. Электрон испускается верхней пластиной конденсатора с нулевой скоростью. Напряженность поля между пластинами 6 10⁵ В/м, расстояние ─ 5 мм. Найти: 1) силу, действующую на электрон; 2) ускорение электрона; 3) скорость, с которой электрон подлетает ко второй пластине; 4) плотность заряда на пластинах.

ДАНО: E = 6 10⁵ В/м, V₀ = 0, d = 0,05 м.

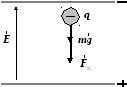ОПРЕДЕЛИТЬ:F_К , a , V, .

РЕШЕНИЕ

1. На частицу с зарядом q в электрическом поле горизонтально расположенного конденсатора действуют две силы: mg — сила тяжести и F_К = q E — кулоновская сила со стороны поля.

Рис. 5

Результирующая этих сил равна: F = mg + q E.

2. Из второго закона Ньютона, определяем ускорение электрона:

.

2. Движение электрона — равноускоренное с ускорением а и начальной скоростью, равной нулю. Поэтому:

,

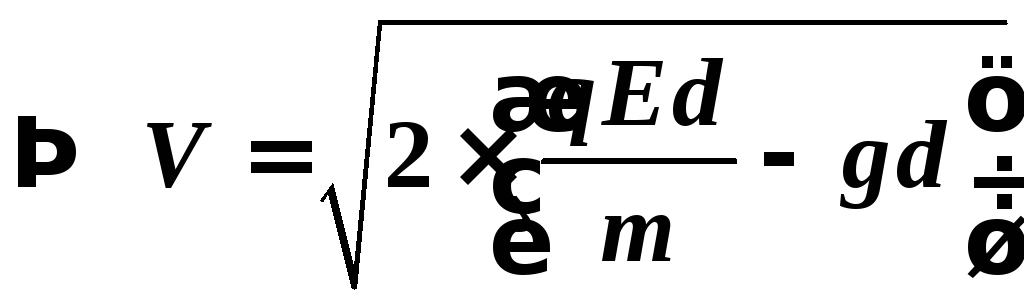где d — расстояние между пластинами.

4. Плотность заряда на пластине конденсатора найдем из формулы напряженности поля плоского конденсатора:

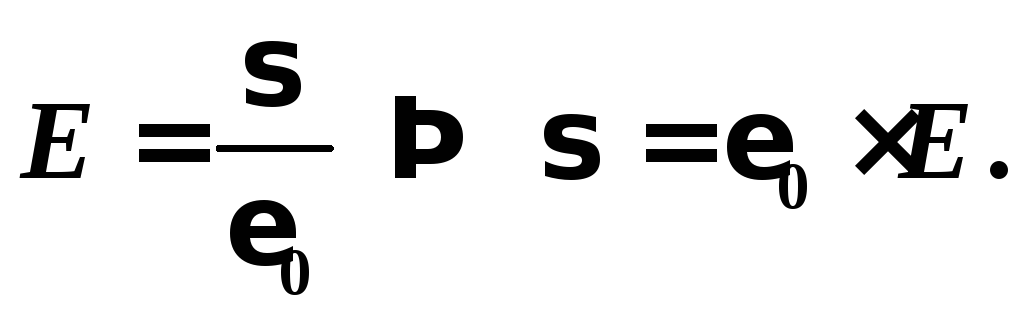
Вычисления: Силой тяжести mg вследствие её малости можно пренебречь.

F = 1,610^-19610⁵ = 9,610^-14 (Н).

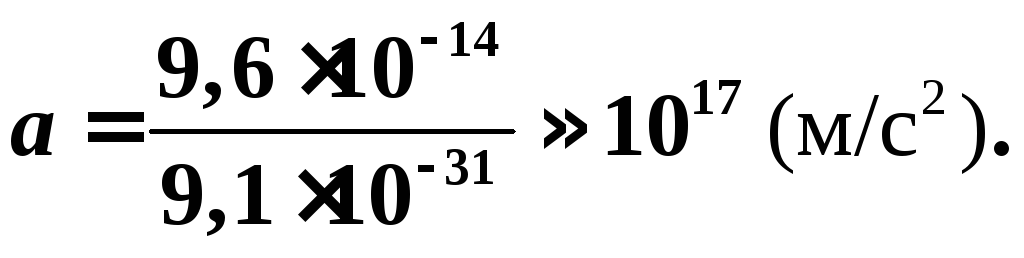
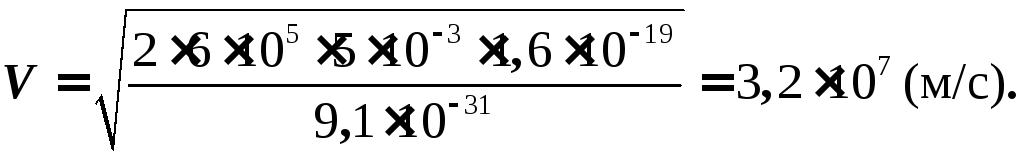
Задана 8. В пространство между двумя параллельными заряженными пластинами, помещенными в вакуум, параллельно им влетает электрон со скоростью V₀ . На расстоянии L скорость электрона отклоняется на угол α от первоначального направления. Найти напряженность поля конденсатора.

РЕШЕНИЕ

На заряд действует сила Кулона

F = q E,

поэтому электрон приобретает ускорение вдоль оси OY :

. (1)

Рис.6

Рис.6

Скорость электрона вдоль оси Y :

. (2)

Вдоль оси X электрон движется с постоянной скоростью V₀. Время t , за которое электрон пройдет расстояние L: . (3)

Подставив (3) в (2), получим: 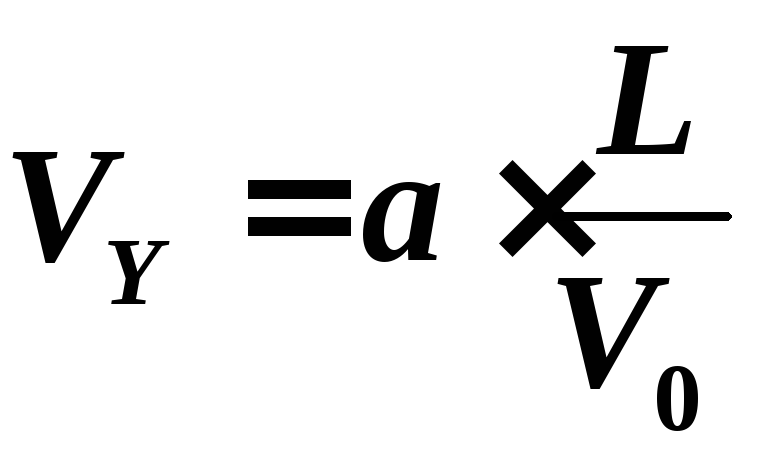. (4)

С другой стороны, можно выразить из треугольника скоростей (см. рис.6):

. (5)

Из формул (4) и (5) находим:

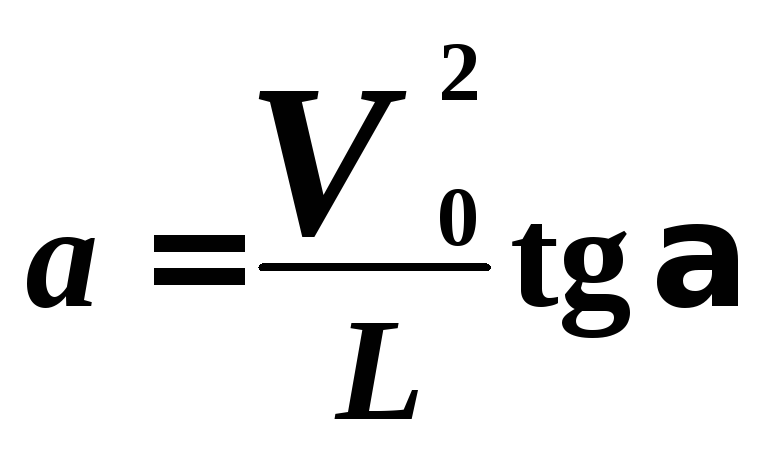. (6)

Напряженность электростатического поля конденсатора E выразим из соотношения (1) с учетом (6):

.

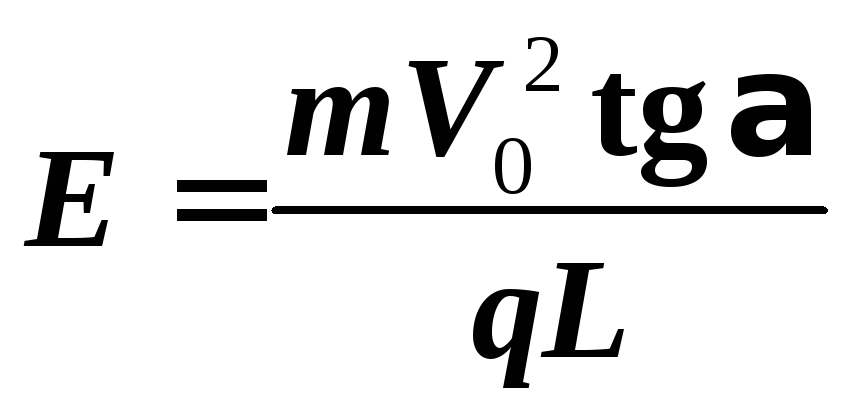Проверка размерности: :

4. Электроемкость

Задача 9. Тысяча одинаковых наэлектризованных капель сливаются в одну, причем их общий заряд сохраняется. Как изменится общая электрическая энергия капель, если считать, что капли сферические и маленькие капли находились на большом расстоянии друг от друга?

РЕШЕНИЕ:

Обозначим через радиус, емкость, энергию и заряд одной капли до слияния; радиус, емкость, энергию и заряд большой капли. Приравняем объем капель после и до слияния:

,

откуда ,

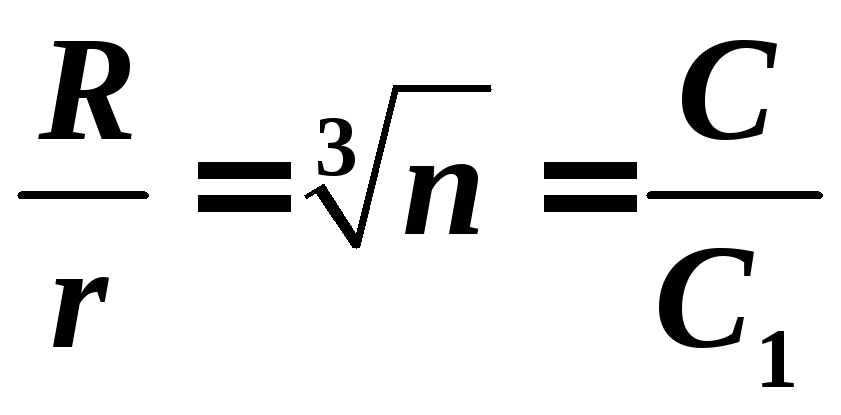где n — число маленьких капель, — емкость шара.

Электрическая энергия одной капли до слияния .

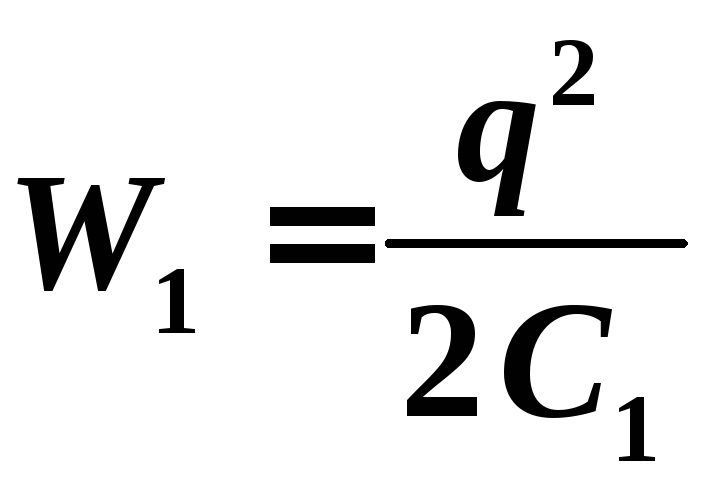Энергия n капель в n раз больше и равна .

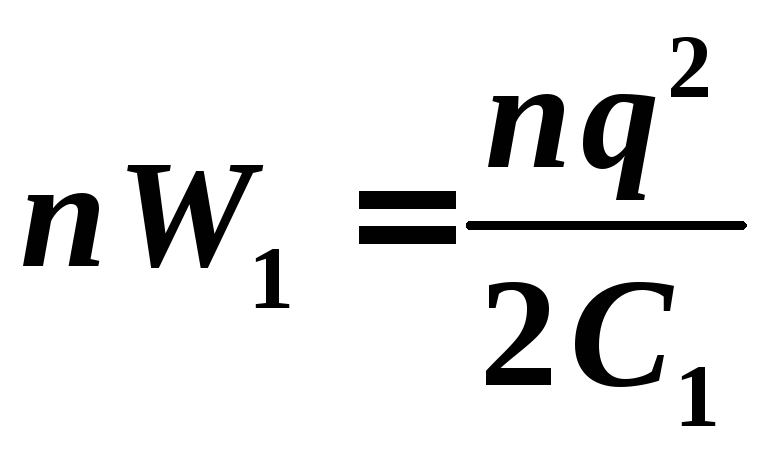Энергия капели после слияния равна .

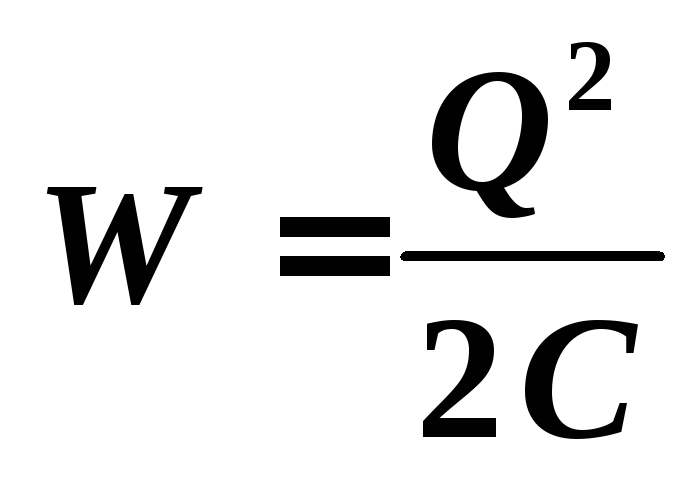Отношение .

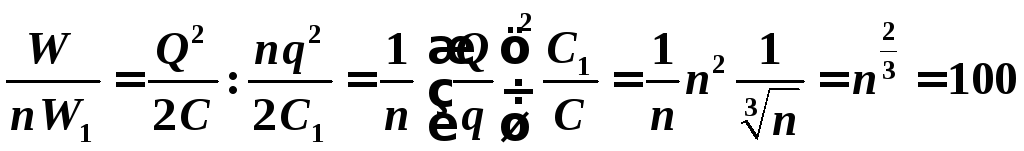Энергия увеличилась в 100 раз.

Задача 10. Батарея конденсаторов сделана из четырех слюдяных пласти­нок толщиной d = 0,1 мм и площадью S = 100 см² каждая из пластинок станиоля (проводник). Сколько понадобилось пластинок станиоля (n) при параллельном соединении батареи? Начертить схему соединения. Опре­делить емкость батареи. Определить запас электрической энергии, если батарея подключена к источнику на­пряжения U = 220 В. Диэлектрическая проницаемость слюды ε = 7.

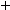
Станиоль

Рис. 7

РЕШЕНИЕ

При параллельном соединении конденсаторов между собой соединяются все положительные и все отрицательно заряженные пластинки станиоля. Каждая пластинка станиоля может служить обкладкой двух соседних конденсаторов, как показано на втором рисунке. Количество пластинок станиоля n = 5. Общая емкость C = nC₁ , где C₁ — емкость одного конденсатора: . Общая емкость.

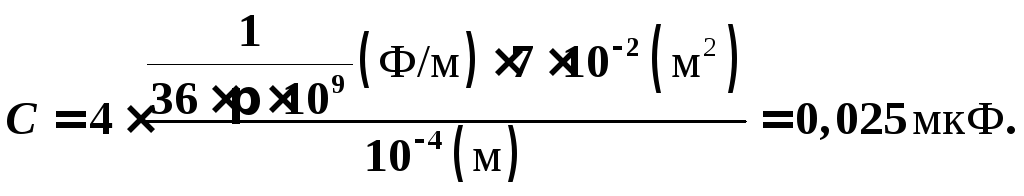
Энергия батареи конденсаторов: