
ИССЛЕДОВАНИЕ ОДНОФАЗНОЙ ЦЕПИ СИНУСОИДАЛЬНОГО ТОКА
.docxЗАДАНИЕ НА РАСЧЁТНО-ГРАФИЧЕСКУЮ РАБОТУ
Начертить схему замещения электрической цепи с обозначением характера сопротивлений всех ветвей.
Указать на схеме условные положительные направления токов в ветвях. Определить токи всех ветвей в комплексной форме.
Определить показания приборов.
Построить векторную диаграмму токов и напряжений на комплексной плоскости.
Построить осциллограмму тока на резисторе, Z3.
Составить баланс активных и реактивных мощностей.
Исходные данные:
Z1=5∙e-j∙90 (Ом);
Z2=9∙e-j∙90 (Ом);
Z3: R=9 Ом, C=318 мкФ;
Z4: R=5 Ом, C=637 мкФ;
Z5: j∙4 (Ом);
u(t)=283∙sin(ωt+π/3) (B).
f = 50 (Гц).
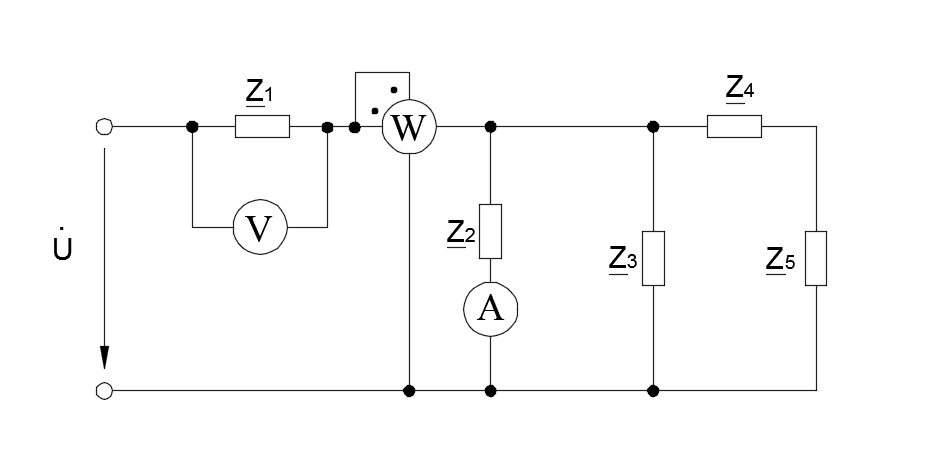
Рисунок 1- Исходная схема.
Решение:
Угловая частота колебаний в цепи:
 (рад/с).
(рад/с).
Определим комплексные сопротивления всех элементов цепи, при этом будем считать, что измерительные приборы идеальные, т. е. сопротивление амперметра равно нулю, а сопротивление вольтметра – бесконечности.
 (Ом);
(Ом);
 (Ом);
(Ом);
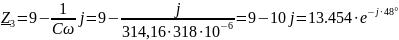 (Ом);
(Ом);
 (Ом);
(Ом);
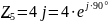 (Ом).
(Ом).
Изобразим схему замещения электрической цепи с обозначением характера сопротивлений ветвей (Рисунок 2).

Рисунок 2 - Схема замещения электрической цепи с обозначением характера сопротивлений ветвей
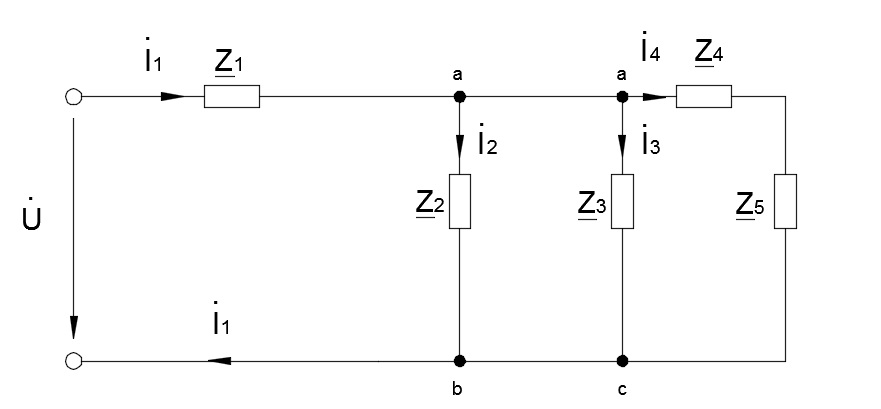 Рисунок
3 - Схема замещения электрической цепи,
на которой все элементы цепи заменены
их изображениями в комплексной форме
Рисунок
3 - Схема замещения электрической цепи,
на которой все элементы цепи заменены
их изображениями в комплексной форме
Упростим схему (Рисунок 4). Сопротивления Z4 и Z5 соединены последовательно.
 (Ом).
(Ом).

Рисунок 4- Схема после первого преобразования.
Сопротивления Z45, Z2 и Z3 соединены параллельно.

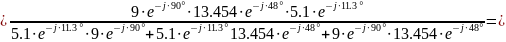
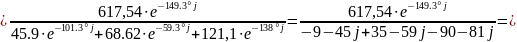
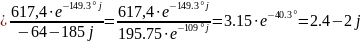 (Ом).
(Ом).
Получим упрощенную схему (Рисунок 5).
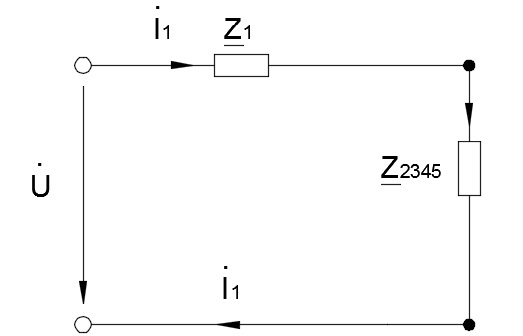
Рисунок 5 - Схема после второго преобразования
Определим эквивалентное сопротивление схемы (Рисунок 6). Сопротивления Z1 и Z2345 соединены последовательно.
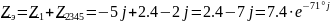 (Ом).
(Ом).
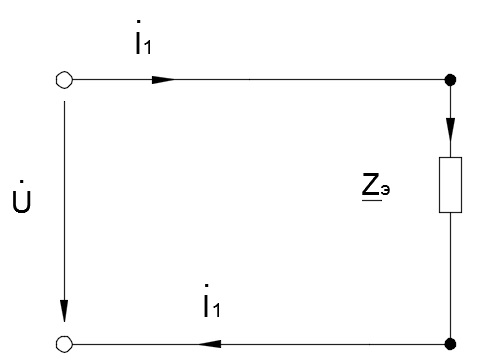
Рисунок 6 – Схема после третьего преобразования
Далее определим эквивалентный ток схемы:
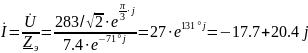 (A);
(A);
 (Ом);
(Ом);
 (Ом);
(Ом);
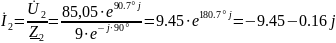 (A);
(A);
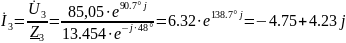 (A);
(A);
 (A);
(A);
 (B);
(B);
 (B).
(B).
Определим показания приборов. Показания приборов представляют собой действующие значения измеряемых величин.
Амперметр показывает действующее значение тока, комплекс которого:
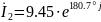 (A).
(A).
Действующее значение – это модуль комплекса тока, т. е. амперметр покажет значение 9.56 (A)
Вольтметр показывает действующее значение напряжения, создаваемого сопротивлением Z1:
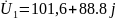 (B).
(B).
Действующее значение – это модуль комплекса напряжения, т. е. вольтметр покажет значение 136.5 (B)
Показания ваттметра- активная мощность, потребляемая сопротивлением Z2345.
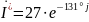 (А)
– сопряженный ток.
(А)
– сопряженный ток.
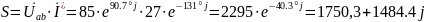
Ваттметр
покажет значение
 Вт.
Вт.
Построим векторную диаграмму токов на комплексной плоскости (Рисунок 7).
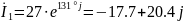 (А).
(А).
 (А).
(А).
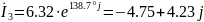 (А).
(А).

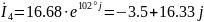
 (А).
(А).
Р исунок 7- Векторная диаграмма токов
Построим векторную диаграмму напряжений на комплексной плоскости (Рисунок 8).
 (Ом);
(Ом);
 (Ом);
(Ом);
 (Ом);
(Ом);
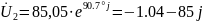 (Ом);
(Ом);

 (Ом);
(Ом);
 (Ом);
(Ом);
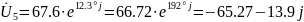 (Ом).
(Ом).
Рисунок 8 - Векторная диаграмма напряжений
Для
построения осциллограммы силы тока
i3(t)
необходимо от найденного нами ранее
изображения этого напряжения в комплексной
форме,
 ,
перейти к её аналитической форме записи.
,
перейти к её аналитической форме записи.
Найдём амплитуду силы тока:
 (A).
(A).
Аналитическая зависимость силы тока будет иметь вид:

Построим таблицу значений для построения осциллограммы в течение одного периода (Таблица 1).
Таблица 1 - Таблица к построению осциллограммы
t |
0.000 |
0.002 |
0.004 |
0.006 |
0.008 |
0.01 |
0.012 |
0.014 |
0.016 |
0.018 |
0.02 |
I3(t) |
5.9 |
0.83 |
-4.56 |
-8.21 |
-8.72 |
-5.9 |
-0.83 |
4.56 |
8.21 |
8.72 |
5.9 |
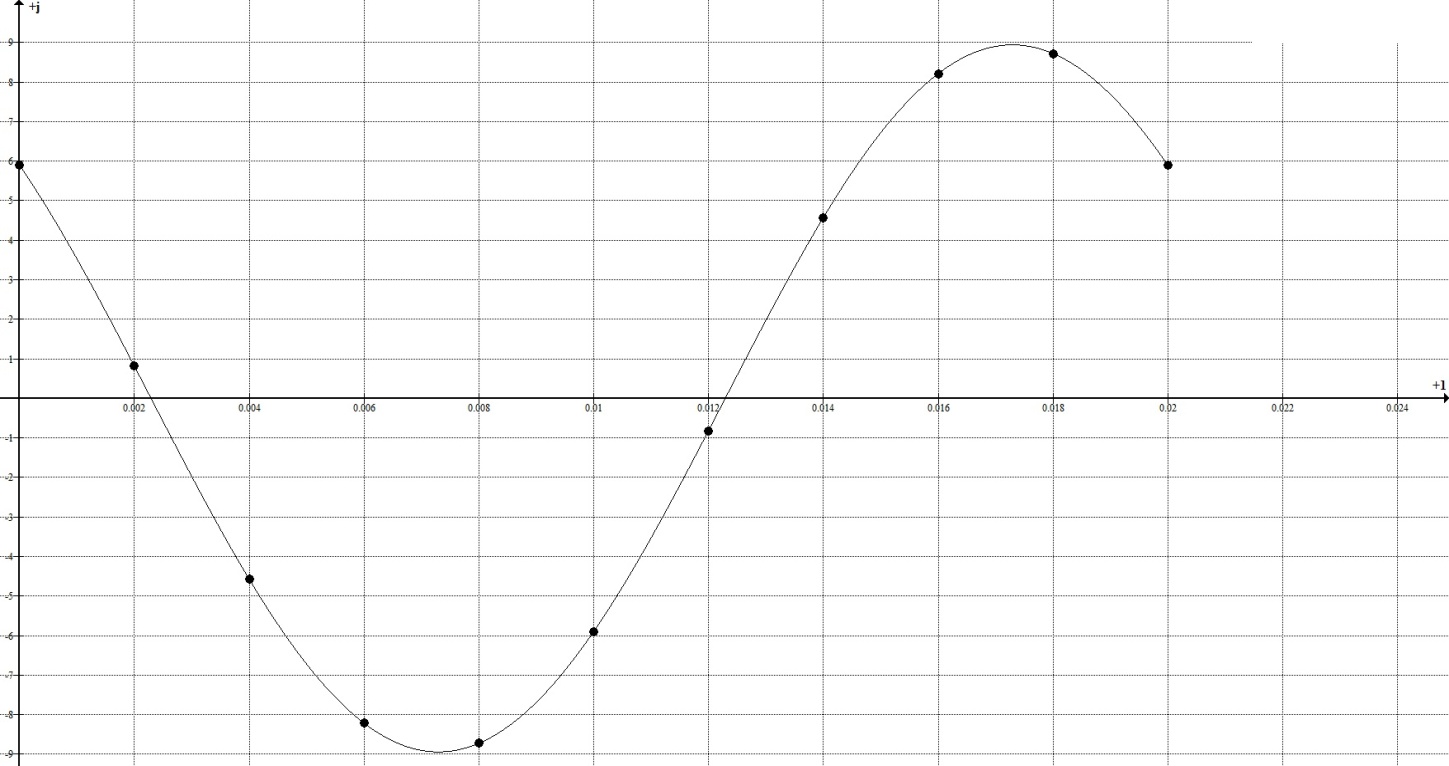
Рисунок 9 - Осциллограмма силы тока i3
Определим полную мощность цепи
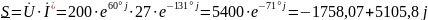
Активная и реактивная мощности, отдаваемые источником энергии:

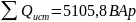
Напряжения и токи были найдены ранее:
(А);
(А);
(А);
(А).
(В);
(В);
(В);
(В);
(В).
Найдем сопряженные комлексные значения силы тока на участках цепи.
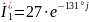
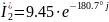
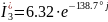
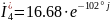
Найдём полные мощности, потребляемые каждым приёмником энергии:
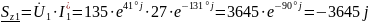 (ВА);
(ВА);
 (ВА);
(ВА);
 (ВА);
(ВА);
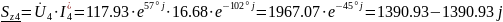 (ВА);
(ВА);
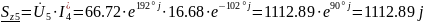 (ВА).
(ВА).
Активная и реактивная мощности, потребляемые каждым приемником энергии:

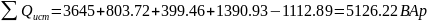
Сравним полученные результаты:

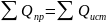
Погрешность вычислений активной мощности:
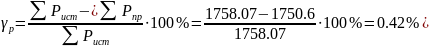
Погрешность вычислений реактивной мощности:
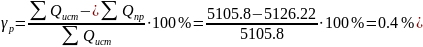
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
Старцев, А. Э. Исследование однофазной цепи синусоидального тока: метод. указания / А. Э. Старцев. – Ухта: Институт управления, информации и бизнеса, 2004. – 44 с. ; ил.
Иванов, И. И. Электротехника и основы электроники: учеб. – 7-е изд., перераб. и доп. / И. И. Иванов, Г. И. Соловьёв, В. Я. Фролов. – СПб.: Лань, 2012. – 736 с. ; ил.
Герасимов, В. Г. Электротехника и электроника : учеб. для студентов неэлектротехнических специальностей вузов. В 3-х кн. Кн. 1. Электрические и магнитные цепи / В. Г. Герасимов [и др.]. М. : Энергоатомиздат, 1996. – 290 с. ; ил.
