
Расчет и конструирование соосного редуктора / 3.2 Расчет косозубой быстроходной передачи
.docx

3.2 РАСЧЕТ ЦИЛИНДРИЧЕСКОЙ КОСОЗУБОЙ ПЕРЕДАЧИ
БЫСТРОХОДНОЙ СТУПЕНИ
Исходные данные:
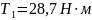 - вращающий момент
на валу шестерни,
- вращающий момент
на валу шестерни,
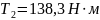 - вращающий момент на валу колеса,
- вращающий момент на валу колеса,
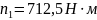 - частота вращения вала шестерни,
- частота вращения вала шестерни,
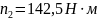 - частота вращения вала колеса,
- частота вращения вала колеса,
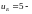 передаточное число цилиндрической
передачи.
передаточное число цилиндрической
передачи.
Режим нагружения передачи - переменный.
Расположение шестерни относительно опор - несимметричное.
Далее по тексту индекс 1 относится к шестерне, а индекс 2- колесу.
3.2.1 Выбор материала и вида термообработки.
По [8, стр.21, табл.3.4] назначаем для колеса Сталь 40Х и для шестерни Сталь 40Х с твердостью
для шестерни 285 HB (термообработка улучшение),
для колеса 250 HB (термообработка улучшение).
Базовое число циклов напряжений [8, стр.41]:
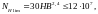 (3.43)
(3.43)
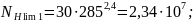
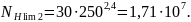
Расчетное число циклов нагружения [1, стр.43]:
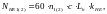 (3.44)
(3.44)
где
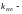 коэффициент
приведения переменного режима нагружения
передачи к эквивалентному постоянному
[1, стр.43]:
коэффициент
приведения переменного режима нагружения
передачи к эквивалентному постоянному
[1, стр.43]:
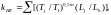 (3.45)
(3.45)
где
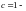 число зацеплений зуба за один оборот
колеса;
число зацеплений зуба за один оборот
колеса;
m=6- показатель степени кривой усталости [2, стр.276].
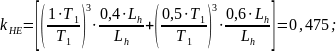
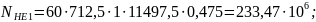
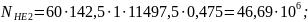
Коэффициент долговечности [2, стр.279]:
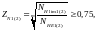 (3.46)
(3.46)
где
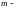 показатель
степени [2, стр.279]:
показатель
степени [2, стр.279]:
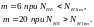
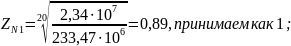
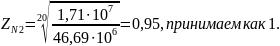
Коэффициент
запаса прочности [8, стр. 40]
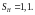
Предел контактной выносливости [8, стр.40]:
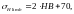 (3.47)
(3.47)
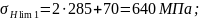
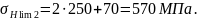
Допускаемое контактное напряжение, МПа [8, стр.40]:
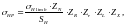 (3.48)
(3.48)
где
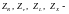 коэффициенты,
учитывающие влияние соответственно
параметров шероховатости активных
поверхностей зубьев, окружной скорости,
вязкости смазочного материала и размеров
колес;
коэффициенты,
учитывающие влияние соответственно
параметров шероховатости активных
поверхностей зубьев, окружной скорости,
вязкости смазочного материала и размеров
колес;
Для предварительных
расчетов ГОСТ 21354-87 рекомендует принимать
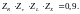
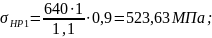
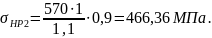
Расчетное допускаемое контактное напряжение [8, стр.42]:
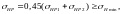 (3.49)
(3.49)
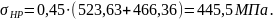
Принимаем
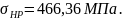
Проверяем условие [8, стр. 42]:
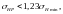 (3.50)
(3.50)
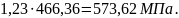
Условие выполняется.
Эквивалентное число циклов напряжений изгиба [1, стр. 43]:
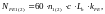 (3.51)
(3.51)
где
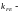 коэффициент
приведения переменного режима нагружения
передачи к эквивалентному постоянному
[1, стр.43]:
коэффициент
приведения переменного режима нагружения
передачи к эквивалентному постоянному
[1, стр.43]:
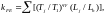 (3.52)
(3.52)
где
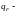 показатель степени [1, стр.43];
показатель степени [1, стр.43];
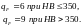
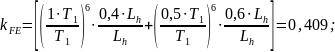
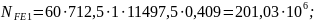
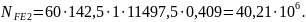
Базовое
число циклов напряжений [1, стр. 43]
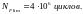
Коэффициент долговечности [2, стр. 281]:
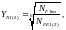 (3.53)
(3.53)
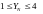 при
HB<=350,
при
HB<=350,
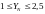 при
HB>350.
при
HB>350.
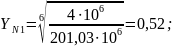
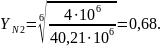
Принимаем
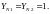
Допускаемое напряжение изгиба [8, стр.42]:
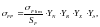 (3.54)
(3.54)
где
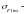 предел выносливости зубьев [2, стр.280]:
предел выносливости зубьев [2, стр.280]:
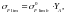 (3.55)
(3.55)
Для отнулевого цикла [8, стр.44]:
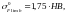 (3.56)
(3.56)
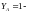 коэффициент
реверсивности [8, стр.43];
коэффициент
реверсивности [8, стр.43];
YТ- коэффициент, учитывающий технологию изготовления; YT=1;
YZ- коэффициент, учитывающий способ получения заготовки зубчатого колеса: поковка и штамповка Yz = 1;
Yg- коэффициент, учитывающий влияние шлифования переходной поверхности зуба; для нешлифованной переходной поверхности Yg = 1;
Yd- коэффициент, учитывающий влияние деформированного упрочнения или электрохимической обработки переходной поверхности; так как этого нет, то Yd = 1;
YR- коэффициент, учитывающий влияние шероховатости переходной поверхности; Yr = 1;
YX- коэффициент, учитывающий размер зубчатого колеса при da ≤ 300 мм, Yx = 1;
Yδ- опорный коэффициент, учитывающий чувствительность материала к концентрации напряжения; для модуля передачи от 1 до 8 мм этот коэффициент убывает от 1,1 до 0,92; примем Yδ = 1;
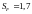 -
коэффициент запаса прочности [8, стр.43].
-
коэффициент запаса прочности [8, стр.43].
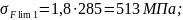
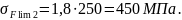
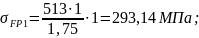
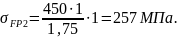
3.2.2 Проектный расчет зубчатой передачи.
Так как редуктор соосный, то межосевое расстояние быстроходной ступени равно межосевому расстоянию тихоходной ступени, т.е.:
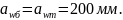
Модуль передачи [8, стр.46]:
 (3.57)
(3.57)
![]()
По ГОСТ 9563-60 [8,
стр.55, табл. 5.5] принимаем
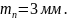
Рабочая ширина венца колеса [8, стр.46]:
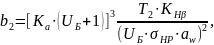 (3.58)
(3.58)
где
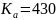 –
расчетный коэффициент;
–
расчетный коэффициент;
где
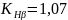 –
коэффициент, учитывающий неравномерное
распределение нагрузки по длине
контактной линии;
–
коэффициент, учитывающий неравномерное
распределение нагрузки по длине
контактной линии;
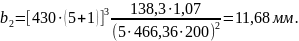
По ГОСТ 6636-69
принимаем
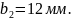
Рабочая ширина шестерни [8, стр.46]:
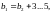 (3.59)
(3.59)
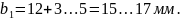
По ГОСТ 6636-69
принимаем
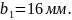
Назначаем
предварительно угол наклона передачи
![]()
Суммарное число зубьев [8, стр.46]:
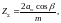 (3.60)
(3.60)
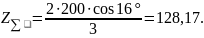
Для дальнейших
расчетов принимаем
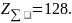
Откорректированный угол наклона зубьев:
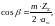 (3.61)
(3.61)
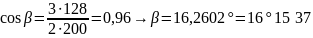
Число зубьев шестерни [8, стр. 47]:
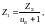 (3.62)
(3.62)
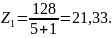
Принимаем
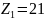 .
.
Тогда число зубьев колеса [8, стр. 47]:
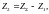 (3.63)
(3.63)
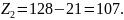
Принимаем
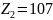 .
.
Фактическое передаточное число:
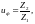 (3.64)
(3.64)
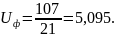
Отклонение от первоначального передаточного числа:
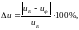 (3.65)
(3.65)
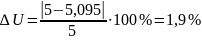 ,
что допустимо.
,
что допустимо.
Делительный диаметр шестерни и колеса [8, стр.47]:
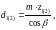 (3.66)
(3.66)
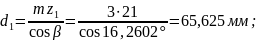
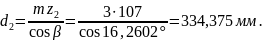
Проверка межосевого расстояния [8, стр.47]:
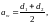 (3.67)
(3.67)
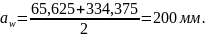
Диаметры вершин зубьев колес:
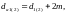 (3.68)
(3.68)
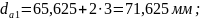
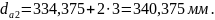
Диаметр впадин зубьев колес:
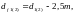 (3.69)
(3.69)
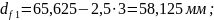
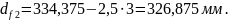
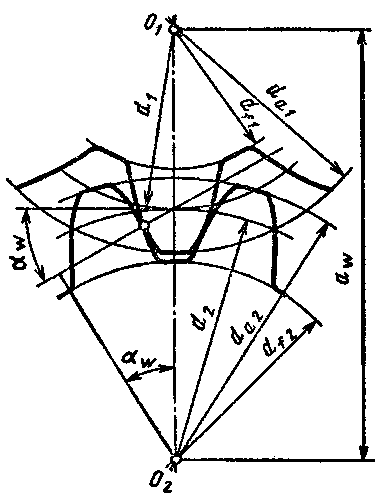
Рисунок 3.3-Геометрия зубчатого эвольвентного зацепления.
Окружная скорость колес [8, стр. 49]:
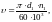 (3.70)
(3.70)
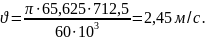
По [8, стр. 55, табл.5.6]
принимаем степень точности
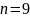 .
.
3.2.3 Расчет составляющих сил в зубчатой передаче [8, стр. 48].
Окружная сила:
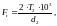 (3.71)
(3.71)
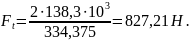
Радиальная сила:
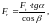 (3.72)
(3.72)
где
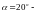 угол
главного профиля по ГОСТ 13754-81.
угол
главного профиля по ГОСТ 13754-81.
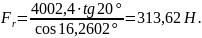
Осевая сила:
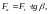 (3.73)
(3.73)
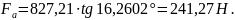
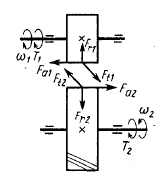
Рисунок 3.3 -Схема сил в зацеплении.
3.2.4 Проверочный расчет зубчатой передачи на прочность.
Контактная
выносливость устанавливается
сопоставлением расчетного
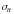 и допускаемого
и допускаемого
 контактных
напряжений [8, стр.48]:
контактных
напряжений [8, стр.48]:
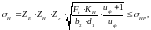 (3.74)
(3.74)
где
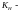 коэффициент
нагрузки в зоне контакта [8, стр.49];
коэффициент
нагрузки в зоне контакта [8, стр.49];
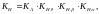 (3.75)
(3.75)
где
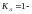 коэффициент,
учитывающий внешнюю динамическую
нагрузку [8, стр. 49];
коэффициент,
учитывающий внешнюю динамическую
нагрузку [8, стр. 49];
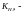 коэффициент,
учитывающий динамическую нагрузку,
возникающую в зацеплении до зоны
резонанса [8, стр. 49]:
коэффициент,
учитывающий динамическую нагрузку,
возникающую в зацеплении до зоны
резонанса [8, стр. 49]:
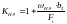 ,
(3.76)
,
(3.76)
где
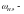 удельная
динамическая сила [8, стр.49]:
удельная
динамическая сила [8, стр.49]:
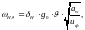 (3.77)
(3.77)
где
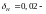 коэффициент,
учитывающий влияние вида зубчатой
передачи и модификацию профиля головок
зубьев [8, стр.56, табл.5.7];
коэффициент,
учитывающий влияние вида зубчатой
передачи и модификацию профиля головок
зубьев [8, стр.56, табл.5.7];
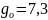 - коэффициент,
учитывающий влияние разности шагов
зацеплении зубьев шестерни и колеса
[8, стр.56, табл.5.8];
- коэффициент,
учитывающий влияние разности шагов
зацеплении зубьев шестерни и колеса
[8, стр.56, табл.5.8];
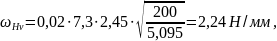
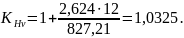
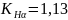 - коэффициент
распределение нагрузки между зубьями
[8, стр.57, табл.5.9].
- коэффициент
распределение нагрузки между зубьями
[8, стр.57, табл.5.9].
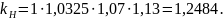
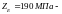 коэффициент
свойства материалов [8, стр.49];
коэффициент
свойства материалов [8, стр.49];
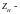 коэффициент,
учитывающий форму зубьев [8, стр.50];
коэффициент,
учитывающий форму зубьев [8, стр.50];
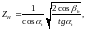 (3.78)
(3.78)
где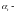 угол
зацепления, для косозубой передачи без
смещения [8, стр.50]:
угол
зацепления, для косозубой передачи без
смещения [8, стр.50]:
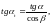 (3.79)
(3.79)
где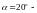 делительный
угол профиля в торцовом сечении [8,
стр.50]:
делительный
угол профиля в торцовом сечении [8,
стр.50]:
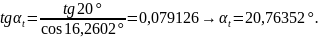
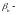 основной
угол наклона для косозубой передачи
[8, стр.50];
основной
угол наклона для косозубой передачи
[8, стр.50];
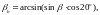 (3.80)
(3.80)
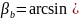
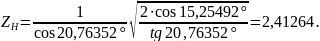
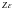 -
коэффициент суммарной длины контактных
линий, при
-
коэффициент суммарной длины контактных
линий, при
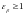 [8, стр.51]:
[8, стр.51]:
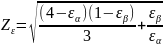 (3.81)
(3.81)
где коэффициент
торцового перекрытия [8, стр.50]:
коэффициент
торцового перекрытия [8, стр.50]:
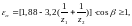 (3.82)
(3.82)
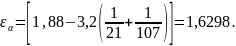
где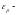 коэффициент
осевого перекрытия [8, стр.50];
коэффициент
осевого перекрытия [8, стр.50];
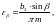 (3.83)
(3.83)
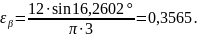

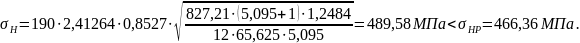
Недогрузка составляет:
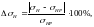 (3.84)
(3.84)
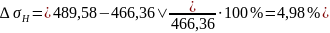
Условие прочности по контактным напряжениям выполняется.
По принятым нормам
[8, стр.51] допускаются отклонения
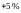 (перегрузка),
и
(перегрузка),
и
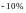 (недогрузка).
(недогрузка).
Проверяем зубья
на выносливость по напряжениям изгиба: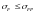 .
.
Расчетное напряжение [8, стр.52]:
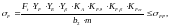 (3.85)
(3.85)
где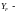 коэффициент,
учитывающий форму зуба, находят в
зависимости от приведенного числа
зубьев
коэффициент,
учитывающий форму зуба, находят в
зависимости от приведенного числа
зубьев
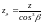 [8, стр.58,
рис.5.5]:
[8, стр.58,
рис.5.5]:
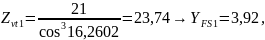
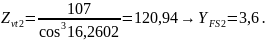
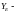 коэффициент,
учитывающий перекрытие зубьев [8, стр.53];
коэффициент,
учитывающий перекрытие зубьев [8, стр.53];
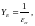 (3.86)
(3.86)
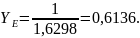
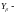 коэффициент,
учитывающий наклон зуба в передаче [8,
стр.52];
коэффициент,
учитывающий наклон зуба в передаче [8,
стр.52];
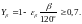 (3.87)
(3.87)
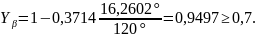
Принимаем
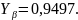
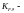 коэффициент
динамической нагрузки [8, стр. 52]:
коэффициент
динамической нагрузки [8, стр. 52]:
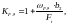 (3.88)
(3.88)
где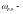 удельная окружная динамическая сила
[8, стр.52]:
удельная окружная динамическая сила
[8, стр.52]:
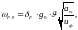 (3.89)
(3.89)
где
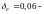 значение коэффициента, учитывающего
влияние вида зубчатой передачи и
модификации профиля зубьев [8, стр.56,
табл.5.7];
значение коэффициента, учитывающего
влияние вида зубчатой передачи и
модификации профиля зубьев [8, стр.56,
табл.5.7];
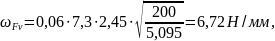
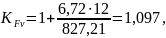
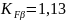 - коэффициент
распределения нагрузки по ширине венца
[8, стр.57, рис.5.4];
- коэффициент
распределения нагрузки по ширине венца
[8, стр.57, рис.5.4];
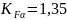 - коэффициент
распределение нагрузки [8,
стр. 56, табл. 5.9].
- коэффициент
распределение нагрузки [8,
стр. 56, табл. 5.9].
Находим отношение
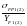 и дальнейший расчет ведем для того
колеса, у которого это отношение меньше
[8, стр.53]:
и дальнейший расчет ведем для того
колеса, у которого это отношение меньше
[8, стр.53]:
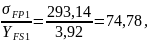
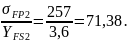
Проверяем прочность зуба колеса:
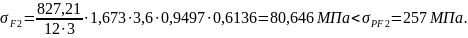
Условие прочности по напряжениям изгиба выполняется.
3.2.5 Расчет передачи при перегрузках
3.2.5.1 Расчет по контактным напряжениям
Максимальные контактные напряжения, создаваемые наибольшим вращающим моментом из числа подводимых к передаче, даже при однократном действии его на зуб, определяются по формуле [2, стр.282]:
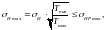 (3.90)
(3.90)
где
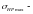 предельно
допускаемое напряжение [2, стр.283]:
предельно
допускаемое напряжение [2, стр.283]:
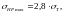 (3.91)
(3.91)
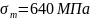 - предел текучести
[8, стр.21, табл. 3.4];
- предел текучести
[8, стр.21, табл. 3.4];
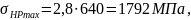
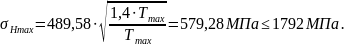
Условие прочности при действии пиковых нагрузок обеспечено.
3.2.5.2 Расчет по напряжениям изгиба.
Для предотвращения хрупкого разрушения или остаточных деформаций зубьев должно выполняться условие [2, стр.283]:
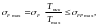 (3.92)
(3.92)
где
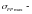 предельно
допускаемое напряжение [2, стр.283];
предельно
допускаемое напряжение [2, стр.283];
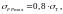 (3.93)
(3.93)

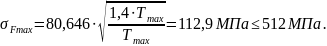
Условие прочности при действии пиковых нагрузок обеспечено.
По соображениям
прочности колес во время термообработки,
ширину колес
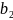 и
и
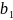 было
решено принять равной
было
решено принять равной
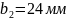 и
и
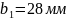 .
.
