Центр ди танционного
Взаимная рекурсияоб чения
•Определение: форма рекурсии, где два математических или вычислительных объекта определены в терминах друг друга. Очень часто в некоторых проблемных областях, таких как
рекурсивный спуск парсеров
• Пример:
(Метод рекурсивного –способ реализации алгоритма
нисходящего синтаксического анализа при реализации компиляторов)
function1()
{
//do something f2();
//do something
}
function2()
{
//do something f1();
//do something
}
online.mirea
.ru
Взаимная рекурсияЦентр дистанционного
обучен
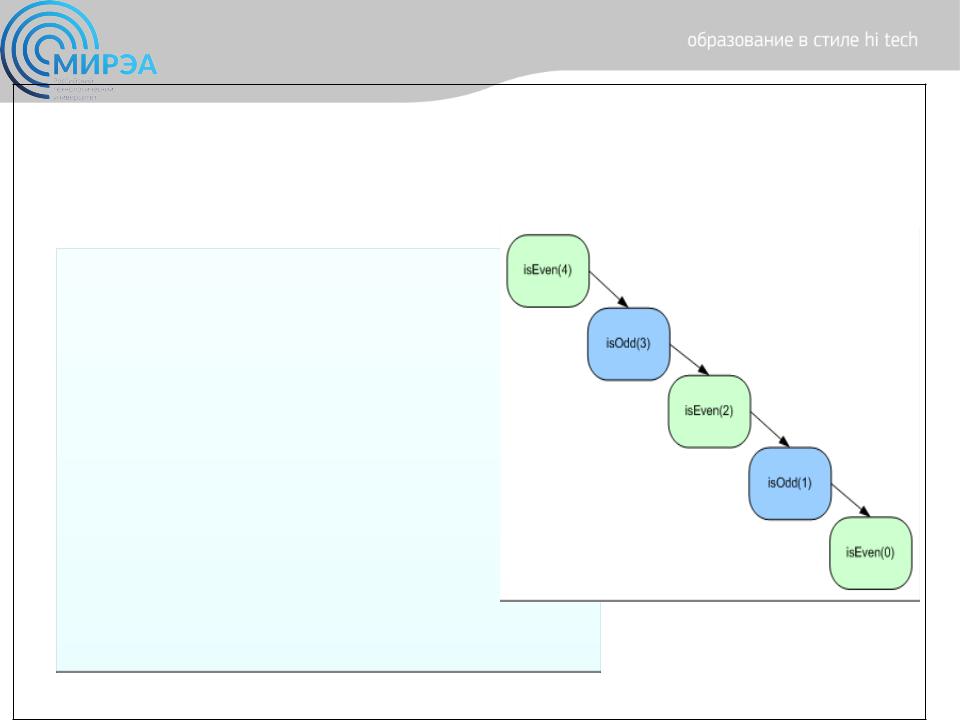
•Стандартный пример взаимной рекурсии (по общему признанию, искусственный) заключается в определении, является ли неотрицательное целое число четным или нечетным.
•Использует две отдельные функции и вызова друг с другом, каждый раз, когда декремента:
boolean even( int number )
{
if( number == 0 ) return true;
else
return odd(Math.abs(number)-1);
}
boolean odd( int number )
{
if( number == 0 ) return false;
else
return even(Math.abs(number)-1);
}
online.mirea
.ru
Центр дистанционного
Взаимная рекурсияобучения
•Хитрый, но совсем не эффективный, пример вычисления чисел Фибоначчи использованием взаимной рекурсии на примере:
int Babies(int n) |
|
{ |
|
if(n==1) |
|
return 1; |
|
else |
|
return Adults(n-1); |
|
} |
|
int Adults(int n) |
|
{ |
|
if(n==1) |
|
return 0; |
|
else |
|
return Adults(n-1) + Babies(n-1); |
|
} |
|
int Fib_Mutual_Rec(int n) |
|
{ |
|
return Adults(n) + Babies(n); |
|
// return Adults(n+1); // is also valid |
|
// return Babies(n+2); // is also valid } |
online.mirea |
|
.ru |
Центр дистанционного
Примитивнаяобучрекурсияния и не примитивная
• Все рекурсиипримеры, которые мы видели до этого момента использовали примитивную рекурсию.
• Не примитивная рекурсия (рекурсия 2 порядка) для вычисления функции Анкермана:
|
ì |
n+1, |
if |
|
m=0 |
|
Ackerman(m,n) = |
íï |
Ack(m- 1,1), |
if |
m¹0 |
and |
n =0 |
|
ï |
|
if |
m¹0 |
and |
n ¹0 |
|
îAck(m- 1, Ack(m, n- 1)), |
|||||
online.mirea
.ru
Центр дистанционного
обучения
Ловушки и Недостатки рекурсии
• Ловушки рекурсии
|
Нет никакой гарантии сходимости – ошибка включать внутрь рекурсивной |
|
функции рекурсивный вызов для решения подзадачи, которая таковой на |
|
самом деле не является (не меньше, чем задача). |
|
Чрезмерные требования к пространству - функция рекурсивно вызывает саму |
|
себя чрезмерное количество раз, прежде чем вернуть значение; |
|
Чрезмерное количество вычислений – было проиллюстрировано в |
|
рекурсивном методе Fibonacci который игнорировал, тот факт, что несколько |
|
промежуточных значений Фибоначчи уже были вычислены |
• Недостатки рекурсии
|
Использование рекурсивных методов может занять больше времени при |
|
выполнении(потеря производительности). |
|
Больше динамической памяти используется для поддержки рекурсивных |
|
вычислений (перерасход памяти). |
online.mirea
.ru
Центр дистанционного
обучения
Важное наблюдение!
•Некоторый "механизм безопасности" должен присутствовать в рекурсивном методе (или подпрограмме) для того, чтобы избежать бесконечного цикла.
•Итерационные методы (с бесконечными циклами) прекращаются принудительно из-за превышения времени выполнения.
•Рекурсивные методы (с бесконечными циклами) прекращаются в связи с нехваткой памяти.
online.mirea
.ru
Центр дистанционного
обучения
Спасибо за внимание!
online.mirea
.ru
Центр дистанционного
обучения
Список источников
•https://urvanov.ru/2016/04/14/java-8-перечисления/
•https://riptutorial.com/ru/java/example/601/ объявление-и-использование-базового-перечисления
•http://www.tvd-home.ru/recursion
•http://ermak.cs.nstu.ru/flp/flp_book/2.8.html
•http://study.sfu-kras.ru/DATA/docs/ProgramTheory/recurs/type_rec.htm
3-98 online.mirea
.ru