
3-й семестр / Семинары / 08
.pdf
Практическое занятие8
Ряды Фурье
Теоретический материал
1. Разложение функций в ряд Фурье
Определение. Пусть f(x) – периодическая функция с периодом 2π,
интегрируемая на [-π; π]. Рядом Фурье называется ряд:
|
|
|
|
+ ∑ |
|
( |
cos |
+ sin ) |
|
|
|
|
|
|
|
|
, где коэффициенты определяются |
формулами: |
|
|
|
|||||
= |
1 |
( |
) |
; |
|
|||
= |
1 |
|
( |
)cos |
; |
|||
= |
1 |
|
( |
)sin |
. |
|||
2.Условия сходимости ряда Фурье
Теорема Дирихле устанавливает условия сходимости ряда Фурье.
Теорема Дирихле. Пусть 2π –– периодическая функция ( ) на
отрезке [− ; ] ([0;2 ]) удовлетворяет двум условиям:
1)( ) –– кусочно-непрерывная, т.е. непрерывная или имеет конечное число точек разрыва I рода;
2)( ) –– кусочно-монотонная, т.е. монотонная на всем отрезке, либо этот отрезок можно разбить на конечное число интервалов так, что на каждом из них функция монотонная.
Тогда соответствующий функции |
( ) |
ряд Фурье сходится на этом |
||||||||
отрезке и при этом: |
|
|
|
|
( |
) |
|
|
|
|
1) в точках непрерывности функции сумма ряда |
совпадает с |
|||||||||
самой функцией: |
; |
|
|
( ) = ( |
) ( |
) |
||||
2) в каждой точке( ) = |
1 |
|
|
|
||||||
(разрыва) |
функции |
|
|
|
|
|
|
, |
||
|
|
|
|
|
|
|||||

сумма ряда равна среднему арифметическому пределов функции |
( |
|
) |
справа |
|||||||||||||||||
ит.еслева. |
; |
|
|
= − и |
= |
|
|
(или при = 0 , = 2 |
|
|
|
||||||||||
3) в точках |
|
|
|
на концах отрезка) |
|||||||||||||||||
(− ) = ( ) = |
( |
) |
( |
|
) |
. |
|
|
|
|
|
|
|
|
|||||||
Таким образом, если функция |
] |
удовлетворяет условиям 1 и 2 теоремы |
|||||||||||||||||||
Дирихле, то на отрезке |
[− |
; ] |
[0;2 |
|
|
|
|
|
|
|
|
||||||||||
|
|
( |
|
|
|
|
( ))имеет место разложение: |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
( ) = |
|
|
+∑ |
|
cos |
+ |
sin . |
( |
) |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Это равенство может нарушиться только в точках разрыва функции |
и на |
||||||||||||||||||||
В силу |
|
[− ; ] |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
концах отрезка |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
периодичности исходной функции и суммы ряда Фурье может быть |
|||||||||||||||||||
получено указанное разложение во всей области определения функции. |
|
|
|
||||||||||||||||||
Пример 1. Разложить в ряд Фурье функцию |
( ) периода 2π, заданную на |
||||||||||||||||||||
отрезке [− |
; ] формулой |
( |
|
) = |
2 |
при 0 ≤ |
≤ , |
|
|
|
|
||||||||||
Решение. |
|
|
|
|
|
|
|
|
|
|
|
− |
при − |
≤ |
≤ 0. |
|
|
|
|
||
Данная функция |
удовлетворяет условиям Дирихле, т.е. может быть |
||||||||||||
разложена в ряд Фурье( ) |
: |
|
1 |
|
|
1 |
|
|
3 |
|
|||
1 |
|
( ) |
|
|
(− ) |
|
|
|
|||||
= |
|
|
= |
|
|
+ |
|
2 |
= |
2 |
, |
||
|
|
2 |
|
||||||||||

= |
1 |
( )cos |
= |
1 |
(− )cos |
+ |
1 |
2 |
= |
|
|
|
|
|
|
|
интегрируем по частям: |
|
|
|
|
|
||||||||
|
|
|
|
|
= |
|
= |
, |
= |
, |
|
= |
|
|
|
|
||||
1 |
|
|
|
|
1 |
= cos |
, |
= |
1 |
sin . |
1 |
|
|
|||||||
|
|
|
0 |
|
|
|
0 |
|
2 |
|
|
|
|
|
|
|||||
= − |
|
|
|
sin |
− |
+ |
|
cos |
− |
+ |
|
|
|
sin |
0 |
+ |
|
cos 0 |
= |
|
|
|
|
|
|
|
|
||||||||||||||
= − |
1 |
(1 −cos |
) + |
2 |
(cos |
|
−1) = − |
3 |
(1 − (−1) ). |
|
||||||||||
Аналогично находим
= |
|
∫ ( )sin |
= |
|
(−1) . |
|
|
Исходной функции ( ) соответствует ряд Фурье
( ) = |
|
|
|
+∑ |
|
|
|
|
|
|
|
|
((−1) |
|
−1)cos |
+ |
|
(−1) |
sin . |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
Функция |
|
|
непрерывна во всех внутренних точках отрезка |
, |
|
|||||||||||||||||||||||||||||
поэтому, согласно( |
теореме) |
Дирихле, для всех этих точек имеем |
|
|
[− ; ] |
|
||||||||||||||||||||||||||||
равенство |
( ) = |
|
( |
|
|
|
) , т.е. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
||||||||||||
( ) = ( ) = |
|
− |
|
|
|
|
|
|
|
+ |
|
|
+ |
|
+ + |
|
− |
|
+ |
|
|
− |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
( ) ( |
) |
= |
|
|
|
|
|
|
|
= |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
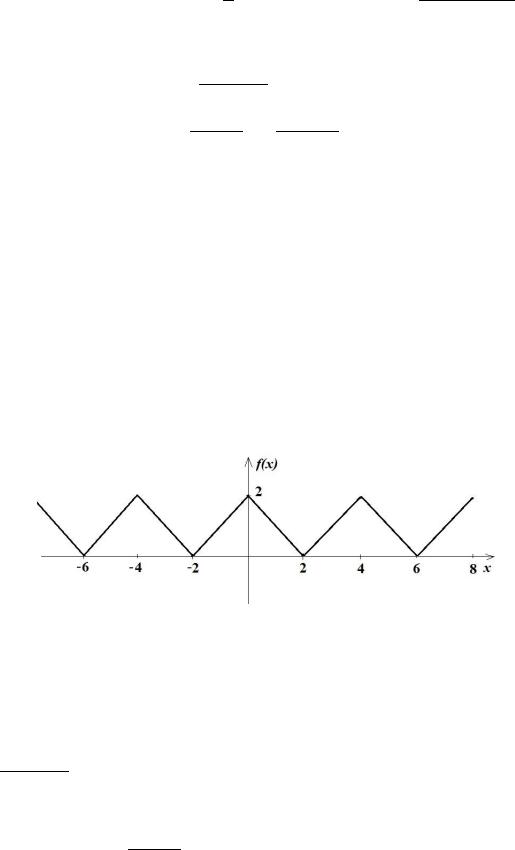
Ниже |
|
|
|
|
|
|
|
|
|
|
( |
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
приведен график |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
3

3. Разложение функции по синусам и косинусам |
|
|||||||||||
Если |
|
– четная функция, тото |
∫ |
( ) |
|
|
( ) . |
|||||
Если |
|
|
. |
|||||||||
|
( ) |
|
|
|
|
∫ |
|
|
= 0 |
|
||
|
( ) – нечетная функция, |
|
|
= 2∫ |
|
|||||||
1) Пусть |
|
– четная функция, заданная( ) |
на полупериоде, тогда |
|||||||||
|
( |
)cos ( |
)– четная функция, а |
( )sin |
– нечетная, |
|||||||
|
|
= |
2 |
( |
) ; |
|
|
|
|
|
|
|
|
|
= |
2 |
( |
)cos |
; |
|
|
|
|
|
|
=0.
Вэтом случае ряд содержит только члены с косинусами и константу
|
. |
( ) – нечетная, |
|
|
|||
|
|
|
|||||
2) Пусть |
функция, заданная. |
на полупериоде, тогда |
|||||
= 0, |
= 0 |
= |
|
|
∫ ( )sin |
|
|
|
|
|
|||||
Вэтом случае ряд содержит члены только с синусами.
4.Ряд Фурье для функции с периодом 2l
Пусть f (x) – периодическая функция с периодом 2l, отличным от 2 .
Разложим функцию f (x) в ряд Фурье. Для этого сделаем замену переменной по
формуле: x l t.
l |
|
|
будет периодической функцией от t с периодом 2π. |
|||||
Тогда функция f |
|
|
|
t |
||||
|
|
|
||||||
|
|
|
|
|
||||
Ее можно разложить в ряд Фурье на интервале , : |
||||||||
l |
|
|
|
a |
|
|||
f |
|
|
t |
0 |
(an cosnt bn sinnt), |
|||
|
2 |
|||||||
|
|
|
|
n 1 |
||||
где
4

|
|
1 |
l |
|
|
|
|
|
|
|
1 |
l |
|
|||||
a0 |
|
|
|
f |
|
|
t dt, an |
|
|
|
|
f |
|
t cosntdt, |
||||
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
1 |
|
l |
|
|
|
|
|
|
|||
|
|
|
|
bn |
|
|
|
|
f |
|
|
t sinntdt . |
||||||
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Вернемся к старой переменной x:
x l t, t x , dt dx.
|
l |
l |
Тогда |
|
|
|
|
1 l |
|
|
|
1 l |
|
nx |
|
|
|
1 l |
nx |
|
|||||||||
a0 |
|
|
|
|
f (x)dx, an |
|
|
|
|
f (x)cos |
|
|
dx, bn |
|
|
|
f (x)sin |
|
dx. |
||||
|
l |
|
l |
l |
l |
l |
|||||||||||||||||
|
|
|
l |
|
|
|
|
|
l |
|
|
|
|
l |
|
||||||||
Разложение Фурье примет вид: |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
a0 |
|
|
|
|
nx |
|
|
|
nx |
|
|
|
||||
|
|
|
|
|
f (x) |
|
|
(an cos |
bn sin |
). |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
2 |
|
n 1 |
|
|
l |
|
|
|
|
|
l |
|
|
||||
Это и есть ряд Фурье для периодической функции с периодом 2l.
Все теоремы, которые имели место для рядов Фурье от периодических
функций с периодом 2 , сохраняются и для рядов Фурье от периодических функций с каким-либо другим периодом 2l. В частности, сохраняет свою силу достаточный признак разложимости функции в ряд Фурье. Также замечание о возможности вычислять коэффициенты ряда, интегрируя по любому промежутку a,b , длина которого равна периоду: 2l b a:
|
|
|
|
2 |
b |
|
|
|
|
|
|
a0 |
|
|
|
f (x)dx, |
|||||||
|
|
||||||||||
|
|
|
b a a |
|
|
|
|
|
|||
|
|
|
|
2 |
|
b |
|
|
2 nx |
|
|
an |
|
|
f x cos |
dx, |
|||||||
|
|
|
|
||||||||
|
|
|
|
b a a |
|
|
b a |
||||
b |
|
|
2 |
b |
f x sin |
2 nx |
dx. |
||||
|
|
|
|
||||||||
n |
|
|
|
|
|
b a |
|||||
|
|
b a a |
|
||||||||
И замечание о возможности упростить вычисление коэффициентов ряда, если функция является четной или нечетной.
5

Если в ряд Фурье разлагается нечетная периодическая функция f (x) с
периодом 2l, то произведение f (x)cos nx есть функция также нечетная, а
l
f (x)sin nx – четная; следовательно, коэффициенты Фурье вычисляются по
l
формулам:
|
|
1 l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
a0 |
|
|
|
|
|
|
|
|
f (x)dx 0, |
|
|
|
|
|
||||||||||
|
|
l |
|
|
|
|
|
|||||||||||||||||
|
|
|
|
l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
an |
|
|
1 l |
f (x)cos |
|
|
nx |
|
dx 0, |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
l |
|
|
|
l |
|
|
|
|
||||||||||||||
|
|
|
|
|
l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
bn |
|
|
2 l |
f (x)sin |
nx |
|
dx. |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
l |
|
|
|
l |
|
|
|
|
||||||||||||||
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
Если в |
ряд |
Фурье разлагается четная функция, то произведение |
||||||||||||||||||
f (x)sin |
nx |
|
есть |
|
|
|
функция нечетная, а f (x)cos |
nx |
– четная и, |
|||||||||||||||
l |
|
|
|
l |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
следовательно, |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
bn |
|
1 l |
f (x)sin |
nx |
dx 0, |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
l |
|
|
|
l |
|
|
|
||||||||||||||||
|
|
|
l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
2 l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
a0 |
|
|
|
|
|
|
|
|
f (x)dx, |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
l |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
an |
|
|
|
2 l |
|
f (x)cos |
nx |
|
dx. |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
l |
|
|
|
|
l |
|
|
|
||||||||||||||
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Примеры разложения в ряд Фурье.
Пример 1. Разложить в ряд Фурье функцию ( ) = − 5 на
(−2,2), = 2.
Решение. Функция – четная, следовательно,
= 0,
6
= |
|
|
∫ ( − 5) = |
|
|
∫ ( − 5) = ( |
|
|
− 5 ) = 2 −10 = −8. |
|
||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
−10 |
|
2 |
|
|||
= |
( − 5) |
|
|
|
|
|
= |
( − 5) |
|
|
|
= |
2 |
+ |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
0 |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
0 ,если |
= 2 |
; |
|
|
|
|
|
|
|||||||
+ |
|
|
|
|
|
|
|
− |
∫ |
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
( |
|
) |
,если |
= 2 +1. |
|
|
|
|
||||||||||||
|
− 5 = −4 − |
|
∑ |
( |
) |
|
( ) |
. |
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
Так выглядит разложение в ряд Фурье.
Пример 1. Разложить функцию |
, заданную на отрезке |
|
|
косинусам и в тригонометрический |
|||
в тригонометрический ряд Фурье(по) = 2 − |
|
|
[0,2] |
ряд Фурье по синусам. |
|
|
|
Решение. Разложение по косинусам. |
[−2,0] |
|
|
продолжим ее на всю числовую ось как |
четным образом и |
||
Доопределим функцию на промежутке |
|
||
периодическую с периодом
равным 4.
a0= |
|
|
|
∫ (2 − ) = 2, |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
= ((2-x) |
|
|
|
+ |
|
∫ |
|
) = |
||||
an = ∫ (2 − ) |
, |
|
|
|
|
|
|||||||||||||||||
= |
|
0,если |
= 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
( |
) |
,если |
= 2 |
+1. |
|
|
|
|
|
|
|
|
|
|
|
||||||||
Ряд Фурье по косинусам имеет вид:. |
|
|
|
|
|
|
|
||||||||||||||||
( ) = |
|
+ |
|
∑ |
|
( ) |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
7 |
|
|
|
|
|
|
|
|
|
|
|||||||||||
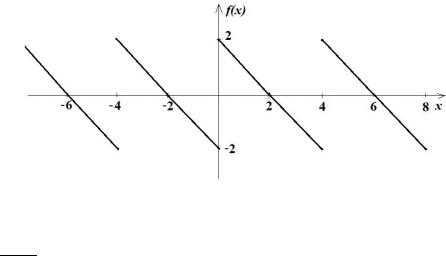
Разложение по синусам.
Доопределим функцию на промежутке [−2,0] нечетным образом и продолжим ее на всю числовую ось как периодическую с периодом равным 4.
= |
|
|
∫ (2 − ) |
|
|
|
= |
|
((2 − )( |
|
)cos |
|
− |
|
∫ |
|
dx) = |
||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||
= |
|
|
− |
( ) |
sin |
|
= |
|
. |
|
|
||||||||||||
|
|
|
|
|
|
||||||||||||||||||
Ряд Фурье по синусам имеет вид:
( ) = |
|
∑ |
|
|
|
. |
|
|
|
Задачи для самостоятельного решения
Типовой расчет для факультетов ИИТ и ФТИ: № 1.14 (1-4, 5-8, 9-12, 13-16); № 2.5 (по номеру варианта).
8
