Добавил:

Rumpelstilzchen Rumpelstilzchen2018@yandex.ru Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

МИРЭА - Российский технологический университет

Предмет:

Математический анализ

Файл:

03-04

.pdf

Скачиваний:

Добавлен:

25.12.2020

Размер:

336 Кб

Скачать

☆

Практические занятия 3, 4

Числовые ряды с положительными членами. Достаточные признаки сходимости. Знакопеременные числовые ряды. Теорема Лейбница. Абсолютная и условная сходимости

Теоретический материал

Числовые ряды с положительными членами. Достаточные признаки сходимости

1. Признак сравнения

∑, тогда: и

∑

Пусть даны два ряда с неотрицательными членами

причем выполняется условие

0 ≤

≤тоже; ≥

а) если

∑

расходится, то

∑

расходится;

сходится, то

∑

тоже сходится.

б) если∑

2. Предельный признак сравнения

= ,где

Пусть даны два ряда с положительными членами:

, то ряды

lim

≠ 0 и

существует конечный и отличный от нуля

→

∑

≠ ∞

∑

сходятся и расходятся одновременно.

3. Признак Даламбера

Пусть дан

ряд.

положительными членами ∑

существует

lim →

< 1 − ряд сходится;

Тогда если

> 1 −ряд расходится;

=1 −требуется дополнительное исследование.

4.Радикальный признак Коши

Пусть дан	ряд	.	с положительными членами ∑	и существует
lim →	=
		< 1 −ряд сходится;
Тогда если	=
		> 1 − ряд расходится;

=1 − требуется дополнительное исследование.

5.Интегральный признак Коши

Пусть дан ряд с положительными членами				, общий член которого
совпадает со значением некоторой	функции		( )	при	= :	= ( )	.
		∑

Предположим, что функция			(	определена, положительна, непрерывна
и монотонно убывает при				.)Тогда:			тоже расходится;
а) если		расходится, то ряд
	( )		≥ 1		∑	∑
∫		сходится, то ряд					тоже сходится.
б) если∫	( )

Примеры

1.Признак сравнения Эталонные ряды

Ряд Дирихле

∑

,если

| ≥ 1 − расходится.

Геометрическая прогрессия

| < 1 − сходится;

∑

,если

> 1 −сходится;

≤ 1 − расходится.

Исследовать на сходимость

∑

√

1.1.Решение.

Проверим необходимый признак сходимости, вычисляя

lim →

√

= lim→

= 0

признак выпол-

- необходимый

lim

→

;∙

нен, продолжаем исследование

Оценим общий член ряда

√

= .

Воспользуемся признаком сравнения.

= 2

∑

- сходится, как ряд

Дирихле с

показателем

ряд с

меньшими членами

тоже сходится по первому признаку

∑ √

сравнения.

∑

cos

Решение.

1.2.

Исследовать на сходимость

Проверим необходимый признак сходимости, вычисляя

lim→

cos

= ∞ (lim →

≠ 0)

необходимому

ряд расходится поlim

→

признаку сходимости.

1.3.

Исследовать на сходимость

∑

Решение.

Проверим необходимый признак сходимости, вычисляя lim →

lim →

необходимый признак выполнен, продолжаем ис-

следование;

Сравним с рядом ∑

который сходится:

≤

∑

- сходится по первому признаку сравнения.

Предельный признак сравнения

Исследовать на сходимость

∑

2.1.

(

Решение.

∑

1 способ: сравним с

- сходится как ряд Дирихле с показателем

α=

;

- сходится по первому признаку срав-

нения.

(

)

≤

∑

(

)

2 способ: сравним с

сходится как ряд Дирихле с показателем

lim

(

)

: = 1

≠ 0

∑

(

)

α=

;

→

∑

ряд

сходится по пре-

дельному признаку сравнения.

2.2.

Исследовать на сходимость

∑

sin

Решение.

Сравним с ∑

прогрессия с

- сходится как

ряд

∑ 2

;

- сходится по

∙

= lim→

lim

sin

предельному→

признаку сравнения.

Исследовать на сходимость

∑

(√

+1 −

2.3.Решение.

)

Проверим необходимый признак:

lim→

= lim→ √

= 0

√

(√

)(√

)

- необходимый признак вы-

полнен, продолжаем исследование;


√ +1 − =	1+	− 1 .
√ +1 − =	1+	− 1 .

Оценим порядок общего члена ряда, для этого воспользуемся таблицей эквивалентных бесконечно малых функций:

( )

−1~

( )

;

( ) → 0.

В нашем

случае ( ) =

Тогда

−1

∙

,т.е. в качестве эталонного ряда возьмем

ряд

Дирихле

(

= 2 > 1), который

сходится.

Вычисляем

lim →

− 1

= lim→

− 1

= lim→

∙

ряд ∑

(√

−

) сходится по предельному признаку.

3. Признак Даламбера

∑

arctg

3.1.Решение.

Исследовать на сходимость

lim→

arctg

= 1∙0 = 0

- необходимый признак выполнен, продолжаем

исследование;

lim→

= lim→

(

)

∙

= 1∙

< 1 ряд сходится по при-

знаку Даламбера.

∑

(

3.2. Исследовать на сходимость

Решение.

Исследование ряда по необходимому признаку затруднительно, поэтому применим сразу признак Даламбера.

Напомним, что (2 +2)! = (2 )!(2 +1)(2 +2).

			(	)!
lim→				( )!

= lim ( )( ) = ∞ > 1 ряд расходится по признаку

→

Даламбера.

3.3. Исследовать на сходимость

∑

(

)

Решение.

∙

(

) = lim→

= 0 < 1

lim→

(

( )(

)

(

)

(

)

ряд сходится по при-

знаку Даламбера.

4. Радикальный признак Коши

4.1. Исследовать на сходимость ∑

√

Решение.

Применим радикальный признак Коши:

lim→

= lim→

= = 0 < 1

√

ряд

сходится

по радикальному признаку Коши.

Исследовать на сходимость

∑

(

)

4.2.Решение.

Применим радикальный признак Коши:

lim→

=lim→

(

)

= lim→

(

)

(

)

= lim→

(

)

> 1 ряд расходится по радикальному признаку Коши.

При использовании радикального признака Коши бывают полезны следующие соотношения:

→

√

→

√

= →

→

= =

Исследовать на сходимость

∑

(

) .

4.3.Решение.

Применим радикальный признак Коши:

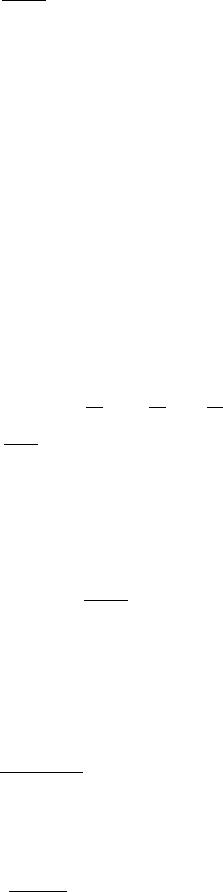
lim→

( ) = lim→

= 0 < 1

ряд сходится по радикальному призна-

ку Коши.

5. Интегральный признак Коши

∑

Исследовать на сходимость

- ряд Дирихле с показателем 5.

5.1.Решение.

Воспользуемся интегральным признаком Коши:

∫

→

∑

= lim −

- сходится

ряд

тоже сходится по ин-

тегральному признаку Коши.

∑

Исследовать на сходимость

5.2.Решение.

Воспользуемся интегральным признаком Коши:

∫

= 2lim→

√

arctg

√

−

- сходится ряд

∑тоже сходится по интегральному признаку Коши.

Исследовать на сходимость

∑

(

) .

5.3.Решение.

Воспользуемся интегральным признаком Коши:

∫

= ∫тоже

= lim→

−

∑

(

)

(

)

- сходится

ряд

(

)

сходится по интегральному признаку Коши.

Задания для самостоятельной работы

Исследовать на сходимость:

1.	∑	(	)		.
2.	∑
2.		sin
4.		sin	.
3.	∑			. .
3.	∑			. .

∑

Домашнее задание: типовой расчет № 1.2-1.5.

Знакопеременные числовые ряды. Теорема Лейбница. Абсолютная и условная сходимости

Теоретический материал

		, называются з		∑	(−1)	∙	или
Определение. Ряды, представленные в виде							или
∑ (−1) ∙	, где	> 0	накочередующимися числовыми ря-
	, где		накочередующимися числовыми ря-

дами.

Теорема Лейбница (признак сходимости знакочередующегося ряда)

Рассматриваем ряд ∑ (−1)

∙ .

а) Если члены знакочередующегося ряда монотонно убывают по модулю:

б) и	≥ ≥	≥ ≥ ≥			,
	стремятся к нулю:		lim →	= 0
то ряд сходится.

Пример. Исследовать на сходимость ряд ∑ (−1) ∙ .

Решение. Проверим выполнения условий теоремы Лейбница:

ба))	=	, начиная,		с номера = 3, верно,	≤ ;

	lim →		= 0

следовательно, ряд сходится по теореме Лейбница.

Абсолютная и условная сходимости

из	∑	- произвольный знакопеременный ряд, а ряд	∑ \| \|	составлен
Пусть		- произвольный знакопеременный ряд, а ряд		составлен

модулей его членов.

Теорема (Коши). Если сходится ряд из модулей членов данного ряда, то сходится и сам знакопеременный ряд.

Определение. Если ряд, составленный из модулей членов данного ряда, сходится, то сам знакопеременный ряд называется абсолютно сходящимся.

Определение. Если знакопеременный ряд сходится, а ряд, составленный из модулей членов, расходится, то такой ряд называется условно сходящимся.

Замечание. При установлении абсолютной сходимости можно пользоваться всеми признаками сходимости положительных рядов.

Примеры

∑

(−1)

1. Исследовать на сходимость

Решение.

Применим

радикальный признак Коши к ряду из модулей:

lim →

= lim→

+3+1

< 1 ряд сходится абсолютно.

2. Исследовать на сходимость ∑

( √

)

Решение. Ряд из модулей является расходящимся как обобщенный гармони-

ческий ряд с показателем = (ряд Дирихле). Однако, для данного ряда

выполнены условия теоремы Лейбница (проверить самостоятельно), следовательно, ряд сходится условно.

Исследовать на сходимость

∑

(−1)

∑

Решение.

Рассмотрим

ряд

из

модулей

по признаку

ра

lim →

(

)

∙

< 1

ряд

= lim→

из модулей сходится, зна-

чит исходный ряд сходится абсолютно.

Исследовать на сходимость

(−1)

Решение. Ряд из модулей будет∑

гармоническим рядом

который рас-

ходится, значит, абсолютной сходимости нет.

Проверим признак Лейбница:

∑

исходный

≤

lim →

= 0

верно

Признак Лейбница

выполняется, значит,

ряд сходится условно.

Замечание. Доказательство монотонного убывания можно проводить одним из трех способов:


а)	непосредственно из свойств функции;
б)	оценивая знак разности				(знак должен быть	);	).
в)	взяв производную от		и	оценив ее знак (знак должен быть			).
в)	взяв производную от		и	−		> 0	< 0
Задания для самостоятельной работы							< 0
Исследовать на сходимость.
1. ∑	(−1)	(Ответ: условная сходимость).
1. ∑	(−1)	(Ответ: условная сходимость).

√

∑

(−1)

Ответ: условная сходимость).

(

)

((Ответ: условная сходимость).

(

∑

(−1)

)

(Ответ: абсолютная сходимость).

∑

(−1)

((√2

−1)

(Ответ: условная сходимость).

∑

(−1)

∑	Ответ: абсолютная сходимость).

Соседние файлы в папке Семинары

#
25.12.2020567 Кб2001.pdf
#
25.12.2020413 Кб1602.pdf
#
25.12.2020336 Кб1603-04.pdf
#
25.12.2020454 Кб1405-06.pdf
#
25.12.2020332 Кб1407.pdf
#
25.12.2020435 Кб1408.pdf
#
25.12.2020457 Кб2212.pdf
#
25.12.2020396 Кб2313.pdf