Добавил:

Rumpelstilzchen Rumpelstilzchen2018@yandex.ru Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

МИРЭА - Российский технологический университет

Предмет:

Математический анализ

Файл:

3-й семестр / Семинары / 02

.pdf

Скачиваний:

Добавлен:

25.12.2020

Размер:

413.07 Кб

Скачать

☆

Практическое занятие 2

Признаки сходимости знакопостоянных рядов. Признаки сравнения. Признак Даламбера.

Определение.

неотрицательны: an

Положительными называются ряды, все члены которых

0 .

Напомним виды рядов, сходимость которых была уже рассмотрена на лекции.



n 1



n 1



n 1

1 n

1
n

q	n

-гармонический ряд – расходится

-ряд Дирихле – сходится при α >1;

расходится при α ≤ 1

- при	q 1	бесконечно убывающая геометрическая прогрессия –

сходится.

Первый признак сравнения. Пусть даны два положительных ряда:

an

n 1

bn

n 1

(1)

(2)

Если для всех номеров n (или для всех номеров n , бóльших некоторого номера N ) выполнено неравенство an bn , то из сходимости ряда (2) следует

сходимость ряда (1), а из расходимости ряда (1) следует расходимость ряда

(2).

Задача 1.

Исследовать на сходимость ряд

ln n

n 2

Решение.

Рассмотрим для

сравнения гармонический

ряд

n 1

который, как уже было доказано,

расходится. Для всех n 2

справедливо

неравенство

и, следовательно, данный ряд также расходится по

ln n

первому признаку сравнения.

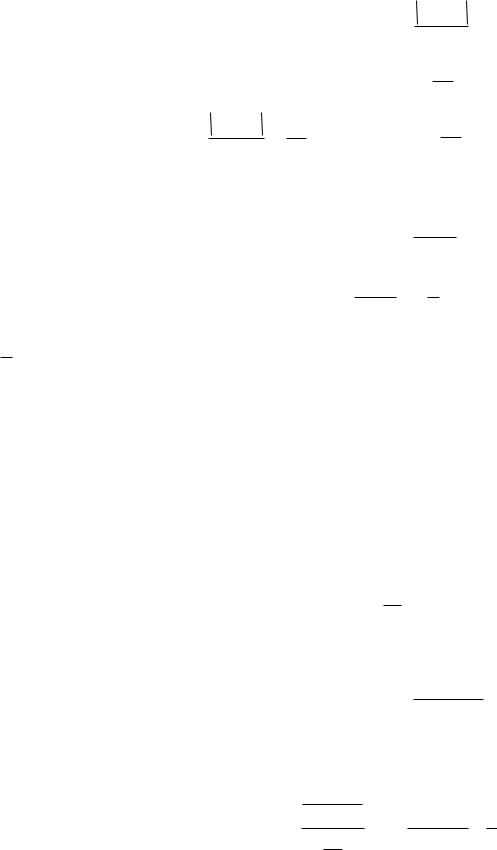
Задача 2. Исследовать на сходимость ряд

Сравним исходный ряд с рядом Дирихле

		cos 3n
			n	3
n 1			n
n 1
			1
			1		. Для всех n
			n	3	. Для всех n
	n 1		n
	n 1

	cos 3n		1				1
выполняется неравенство					. Так как				сходится (ряд

	n	3	n	3			n	3

						n 1

Дирихле, α=3 >1), то исходный ряд сходится по первому признаку сравнения.

Задача 3.

Исследовать на сходимость ряд

n 3

n 1

Для всех

n выполняется неравенство

n 3

сходится (бесконечно убывающая геометрическая

n 1

исходный ряд сходится по первому признаку сравнения.

. Так как ряд

прогрессия), то

Второй признак сравнения (предельный).

положительных ряда:


		an ,
		n 1

bn	, ( bn	0	, начиная с некоторого номера
n 1

Пусть

n ).

даны два

(1)

(2)

Если существует конечный, отличный от нуля сходятся или оба расходятся.

lim	a	n


n b		n

, то ряды (1) и (2) оба

Задача 4. Исследовать на сходимость ряд


Сравним исходный ряд с рядом Дирихле
	n 1
	5

		5

		(2n 1)	2
n 1

1	.	Рассмотрим предел

n2

отношения общих членов этих рядов.			lim	(2n 1)
			lim		1
			n
			n
					n	2
					n
	1
Так как	1	сходится (ряд Дирихле,			α=2
Так как	2	сходится (ряд Дирихле,			α=2
n 1	n

сходится по предельному признаку сравнения.

2		5n	2		5	0
lim		5n			5
lim				2
n (2n 1)				2	4

>1),	то исходный ряд тоже

Задача 5. Исследовать на сходимость ряд

					2
	n	3	2	tg	2
		3
					3	7
n 1				5n		7
n 1

Найдем ряд, с которым надо сравнивать исходный ряд.

n3 2 tg

n3 2

2 n 2

5n3

5n3 7

Проверим,

что

ряд

для

сравнения

2 n

/ 2

lim

Так как

3 / 2

~		1		bn

	n	3 / 2

подобран						правильно.
				1
					сходится (ряд
			n	3 / 2
n 1

Дирихле, α=3/2 >1), то исходный ряд тоже сходится по предельному признаку сравнения.

Задача 6. Исследовать на сходимость ряд

Рассмотрим для сравнения гармонический

arcsin

(

)

10n 2

			3
arcsin	2		3
	2
	10n 2
n 1	10n 2
		1
ряд		1	, так как
ряд		n	, так как
	n 1	n
	n 1

	(	3	)	2
				2
		10n 2			9n	9	0
							0
lim				lim
lim		1		lim		10
n		1		n 10n 2		10

		n

Гармонический ряд

		1

		n
	n 1

расходится,

следовательно, исходный ряд тоже расходится по предельному признаку сравнения.

Задача 7. Исследовать на сходимость ряд


n	2	1/	n 2	1)	5
n		(e		1)
n 1

Найдем ряд, с которым надо сравнивать исходный ряд.

a		n	2	1/	n 2
a	n	n		(e
	n

1)	5

~

	n	2
	n
(	n		2)	5
(	n		2)

	1		b
	1/	2
n			n

Проверим,

что

ряд

для

сравнения

n n

lim

1 .

Поскольку ряд

(n 2)

n1/ 2

подобран правильно.

		1
		1		расходится (ряд
	n	1	/ 2	расходится (ряд
n 1	n
n 1

Дирихле, α=1/2 < 1), то исходный ряд тоже расходится по предельному признаку сравнения.

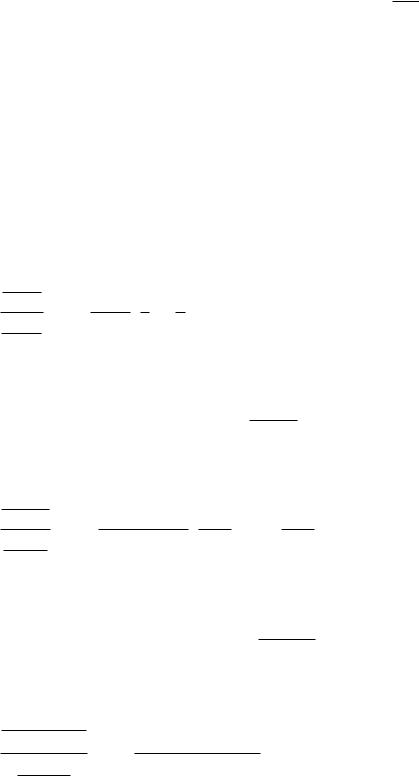
3.2. Признак Даламбера

Если


Теорема. Пусть дан положительный ряд		an	и существует
		n 1
D 1, то ряд сходится, если	D 1 , то ряд расходится.

lim	a	n 1

	a
n			n

Заметим, что если

, то признак ответа не дает.

	3n 5
Задача 8. Исследовать на сходимость ряд				.
Задача 8. Исследовать на сходимость ряд	7		n	.
n 1	7
n 1
Решение. Выпишем n+1 – й член ряда. an+1 =		3(n 1) 5			3n 8
Решение. Выпишем n+1 – й член ряда. an+1 =			7n 1		7n 7
			7n 1		7n 7

Вычислим предел отношения последующего члена ряда к предыдущему

	3n 8
	7	n	7
		n
lim			5
n 3n			5
		7	n
		7

	3n 8	1	1
lim		7	7
n	3n 5	7	7
n

т.е. ряд сходится по признаку Даламбера.

(n 1)!

Задача 9. Исследовать на сходимость ряд

n 1

Вычислим предел

отношения

последующего

предыдущему

(n 2)!

n 1

(n 1)! (n 2)

lim

(n 1)!

члена ряда к

2

Следовательно, ряд расходится по признаку Даламбера.

Задача 10. Исследовать на сходимость ряд



n 1

((n)!)	2

(2n 1)!

Вычислим предел отношения последующего члена ряда к предыдущему

((n 1)!)

(2(n 1) 1)!

((n 1)!)

(2n 1)!

lim

((n)!)

(2n 3)!

(2n 1)!

lim

(n 1)2

n (2n 2)(2n 3)

Следовательно, ряд сходится по признаку Даламбера.

Задача 11. Исследовать на сходимость ряд

		(n 3)!

		(2n)!!
	n 1

Напомним, что (2n)!! – произведение четных чисел от 2-х до 2n, (2n+1)!! – произведение нечетных чисел до 2n+1.

Предел отношения последующего члена ряда к предыдущему

	(n 4)!
lim	(2(n 1))!!	lim	(n 4)! (2n)!!	lim	n 4	1	1
lim		lim		lim			1
n	(n 3)!	n	(n 3)! (2n 2)!!	n	2n 2	2
	(n 3)!		(n 3)! (2n 2)!!		2n 2	2


	(2n)!!

Следовательно, ряд сходится по признаку Даламбера.

Задача 12. Исследовать на сходимость ряд

n 1

Решение. Вычислим

an 1

lim

(n 1)

n 1

lim

(n 1)

n 1

lim

n 1

(n 1)!

2n!

и, согласно признаку Даламбера, данный ряд расходится.

Домашнее задание.

Типовой расчет (3 семестр ИИТ) на сайте кафедры. Задача 1.3. стр.10

№№1-16

Задача 1.4. стр.11

№№1-16

1			1	n	1
	lim					e 1
2		1			2
	n		n

Соседние файлы в папке Семинары

#
25.12.2020566.56 Кб301.pdf
#
25.12.2020413.07 Кб202.pdf
#
25.12.2020335.53 Кб303-04.pdf
#
25.12.2020453.95 Кб205-06.pdf
#
25.12.2020332.01 Кб207.pdf
#
25.12.2020435.1 Кб208.pdf
#
25.12.2020456.57 Кб212.pdf