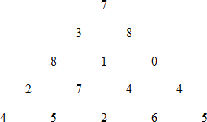3-й семестр / Практические работы / 7 - Стратегии

№

Варианта

Задача

Метод

1

Посчитать число последовательностей нулей и единиц длиныn, в которых не встречаются две идущие подрядединицы.

Динамическое программирование

2

Дана последовательность целых чисел. Необходимо найти ее самую длинную строго возрастающую подпоследовательность.

Динамическое программирование

3

Дана строка из заглавных букв латинского алфавита. Необходимо найти длину наибольшего палиндрома, который можно получить вычеркиванием некоторых букв из данной строки.

Динамическое программирование

4

Имеется рюкзак с ограниченной вместимостью по массе; также имеется набор вещей с определенным весом и ценностью. Необходимо подобрать такой набор вещей, чтобы он помещался в рюкзаке и имел максимальную ценность (стоимость).

Динамическое программирование

5

Дано прямоугольное поле размеромn*mклеток.Можносовершатьшагидлинойводну клеткувправоиливниз.Посчитать,сколькими способами можно попасть из левой верхней клетки в правуюнижнюю.

Динамическое программирование

6

Дано прямоугольное поле размеромn*mклеток.Можносовершатьшагидлинойводну клетку вправо, вниз или по диагонали вправо- вниз. В каждой клетке записано некоторое натуральное число. Необходимо попасть из верхней левой клетки в правую нижнюю. Вес маршрута вычисляется как сумма чисел со всех посещенных клеток. Необходимо найти маршрут с минимальнымвесом.

Динамическое программирование

7

Вычисление значения определенного интеграла с применением численныхметодов.

«Вычислить значение определенного интеграла с заданной точностью определенным методом трапеции. При разработке алгоритма учесть реализацию следующих подзадач в виде функций:

• вычислениезначенияподинтегральной функции в заданнойточкех;

• вычислениезначенияинтеграла установленнымметодомна заданном отрезке интегрирования при nразбиениях;

• вычислениезначенияинтеграла установленнымметодомс заданной точностью.

Динамическое программирование

8

ЧерепашкенужнопопастьизпунктаАвпункт В. Поле движения разбито на квадраты. Известно время движения вверх и вправо в каждой клетке(улицы).Накаждомуглуонаможетповорачиватьтолькона север илитольконавосток. Найти минимальноевремя,

закотороечерепашкаможетпопасть из А вВ.

Динамическое программирование

9

Треугольник. Треугольникимеет вид представленныйнарисунке. Напишитепрограмму, котораявычисляет наибольшую сумму чисел, расположенных на пути начинающемсявверхнейточкетреугольникаи заканчивающегося на основаниитреугольника.

Динамическое программирование

10

Из листа клетчатой бумаги вырезали фигуру ровно по границам клеточек. Разработать программу определения площади вырезанной фигуры.

метода ветвей играниц

11

Разработать программу расстановки на стандартной 64-клеточной шахматной доске 8 ферзейтак,чтобыниодинизнихненаходился под боемдругого».

метода ветвей играниц

12

Разработать программу поиска и вывода всех гамильтоновых циклов в произвольном графе.

метода ветвей играниц

13

Пронумеровать позиции в матрице размером 5*5 следующим образом:если номер i (1<=i<=25) соответствует позиции (x,y), вычисляемым по одному из следующих правил:

(z,w)=(x±3,y)

(z,w)=(x,y≠3)

(z,w)=(x±2,y±2)

1) Написать программу, котораяпоследовательно нумерует позицииматрицы

при заданныхкоординатахпозиции, вкоторой

метода ветвей играниц

поставлен номер 1 (т.е. в некоторой позиции матрицы содержится номер 1).

2) Вычислить число всех возможных расстановок номеров для всех начальных позиций, расположенных под главной диагональю.

14

Замок состоит изкомнат.Сам замок имеетпрямоугольнуюформу и разделен на M*N клеток (M<=50; M>=50). каждая клеткаможетиметь от 0 до 4 стен. Написатьпрограмму, котораяопределяет

• количествокомнатвзамке.

• площадь наибольшейкомнаты

• какуюстену в замке следуетудалить,чтобы получитькомнатунаибольшей площади. Пример плана замка

1 2 3 4 5 67

1

2

3

4

метода ветвей играниц

15

Автозаправка. Вдоль кольцевойдорогирасположеноМгородов.В каждомгородеесть автозаправка. Известна стоимость Z[i] заправкигорючимвгородесномеромi b стоимость C[i] проезда по дороге, соединяющей i-ый и (i+1)-йгородаи стоимость проезда между первым и М-ымгородами.Городапронумерованы по часовой стрелке. Определить для жителейкаждого

города тотгородвкоторомимвыгодно

метода ветвей играниц

заправляться, и направление «по часовойстрелке» или «против часовойстрелки»

16

В массиве размером M˟N , заполненном нулями и единицами найти квадратный блок, состоящий из одних нулей.

метода ветвей играниц

Задача о коммивояжере

метода ветвей играниц

17

Монетная система некоторого государствасостоит из монет достоинством

. Требуется выдать

сумму наименьшим возможнымколичествоммонет.

Жадный алгоритм

18

Разработать процедуру оптимального способа расстановкискобокв произведении последовательности матриц, размерыкоторыхравны (5,10,3,12,5,50,6), чтобыколичествоскалярныхумноженийстало минимальным

(максимальным).

Жадный алгоритм

19

Решить задачу о раскраске вершин графа Применить к задаче управлению светофорами на сложном перекрестке. (Источник постановки задачи - книга: А. Ахо, Д.Хопкрофт, Дж.Ульман Структуры данных и

алгоритмы).

Жадный алгоритм