
3-й семестр / Лекция 2 - Бинарное дерево
.pdfvoid Pereorder (BinTree T){ if( ! Empty(T))
{
Pereorder(LeftTree(T),visit);
Visit(Root(T));
Pereorder(RightTree(T),visit);
}
}
Обход бинарного дерева в обратном порядке
 обойти в обратном порядке левое поддерево
обойти в обратном порядке левое поддерево
 обойти в обратном порядке правое поддерево
обойти в обратном порядке правое поддерево  посетить корневой узел
посетить корневой узел
void Pereorder (BinTree T){
{
If (!Empty(T) )
{
Pereorder(LeftTree(T),visit);
Pereorder(RightTree(T),visit);
Visit(Root(T));
}
}
Пример 5. Использование алгоритмов обхода для создания:
 Польской постфиксной записи выражения Постфиксная запись (знак операции следует за операндами) выражения a+b/с имеет вид abc/+
Польской постфиксной записи выражения Постфиксная запись (знак операции следует за операндами) выражения a+b/с имеет вид abc/+
 Польской префиксной записи выражения Префиксная запись (знак операции указывается перед операндами) выражения a+b/с имеет вид +a/bc
Польской префиксной записи выражения Префиксная запись (знак операции указывается перед операндами) выражения a+b/с имеет вид +a/bc
 Инфиксной записи выражения.
Инфиксной записи выражения.
Инфиксная запись (знак операции между операндами) выражения имеет вид a+b/с
При создании таких форм записи выражения используется алгоритм обхода дерева выражения.
Пусть имеется дерево выражения, представленное на рисунке 7.
Обход дерева выражения в обратном порядке позволяет создать польскую постфиксную запись выражения.
ab+cde/-*
Обход дерева выражения в прямом порядке позволяет создать польскую префиксную запись выражения.
*+ab-c/de
Обход дерева выражения в симметричном порядке позволяет создать инфиксную запись выражения.
(a+b)*(c-d/e)
Пример 6. Использование алгоритма обхода для отображения бинарного дерева на мониторе.
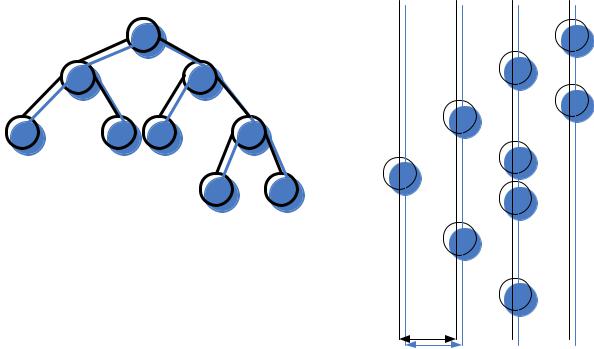
Так как узлов в дереве может быть много, то при выводе на монитор выводить информацию надо построчно, то удобно дерево представить в перевернутом виде, как представлено на рисунке 8 вид 2.
Из рисунка видно, что самым первым выводится правый узел правого поддерева, затем его корень, затем его левый узел и т. д., т.е. выводится правое дерево, затем левое поддерево, опять с самого правого. Из представления дерева видно, что для вывода удобно использовать симметричный обход, только начинать надо с правого поддерева.
Уровни дерева |
0 |
1 |
2 |
3 |
|
|
1 |
|
9 |
|
2 |
|
3 |
7 |
|
|
|
||
|
|
|
|
8 |
|
|
|
|
3 |
4 |
5 |
6 |
|
7 |
|
|
|
|
6 |
|
|
|
|
1 |
|
|
|
8 |
9 |
|
|
|
|
5 |
|
1 |
|
|
2 |
|
|
|
|
|
|
|
|
|
4 |
L
2
Рис. 8. Дерево (1) и вид при выводе на монитор(2)
//выводит дерево level –уровень выводимого узла.
// Количество пробелов от уровня 0 до уровня узла по формуле номер уровня
* L
void printBinTree(BinTree T.int level,int L){ int i;
If (! Empty(T))
{
printBinTree((rightTree(T), level+1,L); for (i=1;i<=level*L; i++ ){
cout<<’ ‘; cout<<Data(T);
printBinTree((LeftTree(T), level+1,L);
}
}
Обход бинарного дерева алгоритмом “в ширину”
Такой обход выводит дерево по уровням. При обходе пройденные узлы записываются в очередь, затем из очереди извлекается узел и обрабатывается, а в очередь отправляются его сыновья (узлы левого и правого деревьев.

Пример 8. Обход дерева в ширину
Рассмотрим алгоритм обхода в ширину на приведенном дереве
|
|
|
|
|
1 |
|
|
|
|
|
|
|
А |
|
|
|
|
|
|
В |
2 |
|
|
3 |
|
|
|
|
|
|
|
С |
|
|
|
D |
4 |
|
E |
F |
|
6 |
7 |
|
5 |
|
G |
|
|||||
|
|
|
||||||
|
|
|
|
|
8 |
H |
J |
9 |
|
|
|
|
|
|
|
|
1)В очередь помещается первый узел с меткой А Очередь
А
2)Из очереди извлекается узел для обработки и в очередь помещаются его сыновья
В |
С |
|
|
3) Из очереди извлекается узел В для обработки и в очередь помещаются его сыновья
|
С |
D |
E |
|
|
|
|
|
|
|
|
4) Из очереди извлекается узел C для обработки и в очередь помещаются его |
|||||
сыновья |
|
|
|
|
|
|
|
|
|
|
|
|
D |
E |
F |
G |
|
|
|
|
|
|
|
5) |
Из очереди извлекается узел D для обработки и в очередь должны |
||||
помещаться его сыновья, но их нет, значит, ничего не помещается |
|||||
|
|
|
|
|
|
|
|
E |
F |
G |
|
|
|
|
|
|
|
6) |
Из очереди извлекается узел E для обработки и в очередь должны |
||||
помещаться его сыновья, но их нет, значит, ничего не помещается |
|||||
|
|
|
|
|
|
|
|
F |
G |
|
|
|
|
|
|
|
|
7)Из очереди извлекается узел F для обработки и в очередь должны помещаться его сыновья, но их нет, значит ничего не помещается
G
8)Из очереди извлекается узел G для обработки и в очередь помещаются его сыновья
НJ
9)Из очереди извлекается узел H для обработки и в очередь должны помещаться его сыновья, но их нет, значит, ничего не помещается
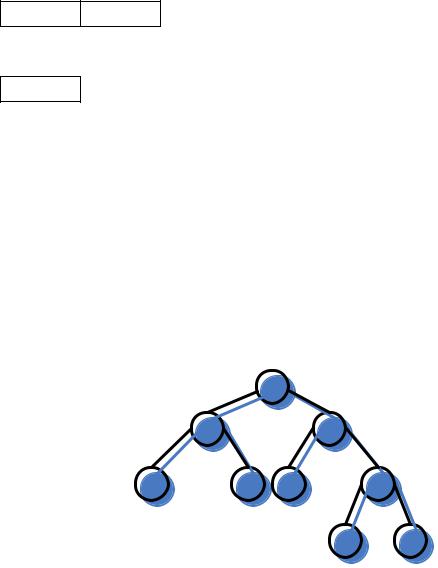
J
10)Из очереди извлекается узел J для обработки и в очередь должны помещаться его сыновья, но их нет, значит, ничего не помещается
11)Очередь пуста, а следовательно, все дерево пройдено.
Реализации бинарного дерева
1.Таблица
Таблица состоит из элементов, включающих ссылку на правое поддерево, левое поддерево и метку узла. Данные по узлам могут храниться в другой структуре данных, например, массив.
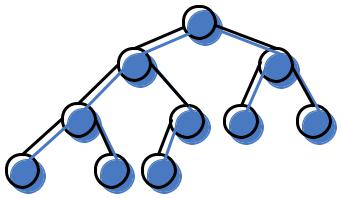
Рассмотрим представление в памяти дерева, элементы которого проиндексированы по мере его добавления.
|
|
|
|
|
1 |
|
|
|
|
|
|
|
А |
|
|
|
|
|
|
В |
3 |
|
|
2 |
|
|
|
|
|
|
|
С |
|
|
|
D |
4 |
|
E |
F |
|
6 |
7 |
|
5 |
|
G |
|
|||||
|
|
|
||||||
|
|
|
|
|
8 |
H |
J |
9 |
|
|
|
|
|
|
|
|
Рис. 9. Бинарное дерево узлы индексированы и имеют метки
В нижеследующей таблице приведена реализация дерева рисунка 9.
Индекс |
LeftTree |
RightTree |
label |
узла |
|
|
|
|
|
|
|
1 |
3 |
2 |
A |
|
|
|
|
2 |
4 |
5 |
B |
|
|
|
|
3 |
6 |
7 |
C |
|
|
|
|
4 |
0 |
0 |
D |
|
|
|
|
5 |
0 |
0 |
E |
|
|
|
|
6 |
0 |
0 |
F |
|
|
|
|
7 |
8 |
9 |
G |
|
|
|
|
8 |
0 |
0 |
H |
|
|
|
|
9 |
0 |
0 |
J |
|
|
|
|
Определение реализации дерева в программе может быть таким:
Type
TNode=record
LeftTree:integer;
rightTree:integer;
Label:Tdata
End;
BinTree=record
Table: array of TNode; Root:integer
N:integer; //количество узлов
End;
2. Массив родителей
Бинарное дерево можно представит в памяти через массив родителей. Массив родителей описан в лекции 7 для сильно ветвящихся деревьев.
Массив для дерева рисунка 9.
0 |
1 |
1 |
2 |
2 |
2 |
2 |
7 |
7 |
|
|
|
|
|
|
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
3. Реализация законченного двоичного дерева
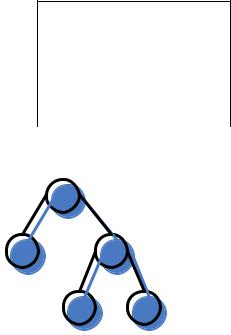
Согласно теории по данному дереву (см. раздел 3 данной лекции), его узлы можно индексировать: корневому узлу присвоить индекс 0, если i – индекс узла, то узел его правого поддерева имеет индекс 2i+2, а узел его левого поддерева будет иметь индекс 2i+1.
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
А |
|
|
|
|
|
|
В |
1 |
|
|
|
2 |
|
|
|
|
|
|
|
С |
|
|
D |
3 |
|
4 |
|
|
|
|
|
|
|
E |
F |
|
G 6 |
||
|
|
|
|
5 |
||||
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
7 |
|
|
|
|
|
|
|
|
H |
|
8 J |
|
I |
9 |
|
|
|
Рис. 10. Индексированное законченное бинарное дерево
Представим массив для хранения дерева на рисунке 10.
А |
В |
С |
D |
E |
F |
G |
H |
J |
I |
|
|
|
|
|
|
|
|
|
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
Определение реализации дерева в программе может быть таким:
Type
BinTree=record
Table: array of TData;
N:integer; //количество узлов
End;
4. Реализация на указателях
Структура узла
Область данных
Ссылка |
Ссылка |
на левое |
на правое |
поддерево |
поддерево |
|
|
Тогда бинарное дерево, со значениями, представляющими метки
С
F G
H J
можно представить в виде структуры, представленной на рисунке 11
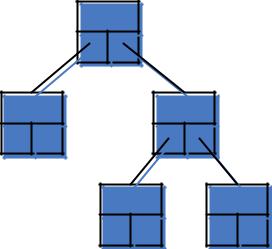
C
F |
G |
nil nil
H |
J |
nil nil
nil nil
Рис.11. Структура бинарного дерева на указателях
Программная реализация узла дерева и дерева указателях.
Type
PointerInTree=^TNode;
TNode=record
Label:TData;
LeftTree: PointerInTree;
RightTree: PointerInTree
End;
Var
Root: PointerInTree; |
//указатель на дерево |
Пример 7. Реализация бинарного дерева на указателях.
unit Unit1;
//В модуле реализованы некоторые операции АТД для бинарного дерева, созданного как //сбалансированное дерево.
interface Type
Tdata=integer;
BinTree=^TNode;
TNode=record
LabelNode:TData;
LeftTree: BinTree;
RightTree: BinTree
End; Tdar=array of Tdata;
procedure CreateNode( var Node:BinTree;labelNode:Tdata );//создание узла
//создание идеально сбалансированного дерева из n узлов
//данные для узла передаются в массиве а, передается индекс первого элемента
Procedure CreateBinTree(var T:BinTree;n:integer;const a:TDar;var i:integer); //указатель на левое поддерево
Function LeftTree(var T:BinTree): BinTree; //указатель на правое поддерево
Function RightTree(var T:BinTree): BinTree;
//отображение бинарного дерева на монитор
Procedure printBinTree(T:BinTree;level,L:integer); Function Empty(var T:BinTree):boolean;
//значение узла дерева Т
Function Data(var T:BinTree):Tdata; implementation
procedure CreateNode( var Node:BinTree;labelNode:Tdata ); begin
New(Node);
Node.LabelNode:=labelNode;
Node.LeftTree:=nil;
Node.RightTree:=nil
end;
Procedure CreateBinTree(var T:BinTree;n:integer;const a:TDar;var i:integer); var
nl,nr:integer; begin
if n<>0 then begin
nl:=n div 2; nr:=n-nl-1;
CreateNode(T,a[i]);
i:=i+1;
CreateBinTree(T^.LeftTree,nl,a,i);
CreateBinTree(T^.RightTree,nr,a,i);
end
end;
Function LeftTree(var T:BinTree): BinTree; begin
result:=T^.LeftTree;
end;
Function RightTree(var T:BinTree): BinTree; begin
result:=T^.RightTree;
end;
Procedure printBinTree(T:BinTree;level,L:integer); Var
I:integer;
Begin
If not Empty(T) then Begin
printBinTree(rightTree(T),level+1,L); for i:=1 to level*L do
write( ' ' ); writeln(Data(T));
printBinTree(LeftTree(T), level+1,L);
end
end;
Function Empty(var T:BinTree):boolean; begin
result:=T=nil
end;
Function Data(var T:BinTree):Tdata; begin
result:=T.LabelNode
end;
end.
//ОСНОВНАЯ ПРОГРАММА program Project2;
{$APPTYPE CONSOLE}
