3-й семестр / Лекция 2 - Бинарное дерево

Лекция 12

Бинарное дерево

Определение.

Дерево Т называется бинарным деревом, если: это пустое дерево либо состоит из одного узла – корня дерева

либо имеет два поддерева – левое и правое, либо имеет одно поддерево: левое или правое, каждое из которых так же двоичное дерево Т.е. бинарное (двоичное) дерево это дерево, степень которого не больше двух.

Пример 1. Двоичное дерево. Определить количество его поддеревьев. Дано дерево представленное на рисунке 1.

А

ДЕ

Рис.1. Бинарное дерево

В данном дереве всего поддеревьев 11: дерево А (является поддеревом самого себя), дерево В, C, D, E и 6 пустых (у листьев).

Левое поддерево дерева А - это дерево с корнем В. Правое поддерево дерева А – это дерево с корнем С.

АТД Бинарное дерево АТД BinTree

Данные

Список узлов дерева Количество узлов в дереве Корень дерева Root

TNode – тип узла

Tdata – тип информационной части узла

Операции

//Создание бинарного дерева

CreateBinTree T);

//левое поддерево дерева Т

LeftTree( T)

//правое поддерево дерева Т

RightTree(T)

//Количество листьев

Leaves(T);

//Номер уровня узла n

Level(n);

//Количество узлов в дереве Т

CountNodes(T);

//Высота дерева Т height(T);

//Прямой обход дерева Т

PreOrderTree(T); //Обратный обход дерева Т

PostOrderTree(T); //Симметричный обход дерева Т

InOrderTree(T);

//Вывод дерева на монитор

Print(T);

//Определения пустого дерева

Empty(T);

//Нахождение родителя узла n

Parent(n);

Root(T);

date(n);

End.

Основные понятия

1. Путь в дереве.

Путь от узла Х до узла У (У есть потомок Х) это последовательность узлов, начинающаяся в Х и заканчивающаяся в У, в которой каждый

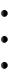
8.Теорема о двоичном дереве

1)В любом двоичном дереве количество листьев ≤ количеству узлов

(Leaves(T) ≤CountNodes(T).

Равенство (Leaves(T) = CountNodes(T) возможно только в случае, если дерево состоит из одного узла – корня.

2)Для раздваивающегося двоичного дерева справедлива формула

Leaves(T)=(CountNodes(T)+1)/2.0

3)Для любого непустого бинарного дерева справедлива формула

Leaves(T) ≤(CountNodes(T)+1)/2.0

А следовательно, справедлива формула

(CountNodes(T)+1)/2.0≤2heigh(T)

Формула 2heigh(T) определяет количество возможных листьев в дереве высотой heigh(T).

4) Если дерево полное, то справедлива зависимость (CountNodes(T)+1)/2.0=2heigh(T). Тогда можно вывести формулы определения количества узлов в дереве через его высоту и высоту через количество узлов:

Количество узлов

CountNodes(T)=2heigh(T) *2-1

Высота дерева heigh(T)=Log2(CountNodes(T)+1)/2.0).

Таким образом, высота дерева логарифмически зависит от количества узлов.

1. Виды двоичных деревьев

1.1.Раздваивающееся бинарное дерево.

Бинарное дерево Т называется раздваивающимся деревом, если:

оно пустое дерево

либо оба его поддерева являются пустыми либо оба поддерева являются непустыми раздваивающимися

деревьями.

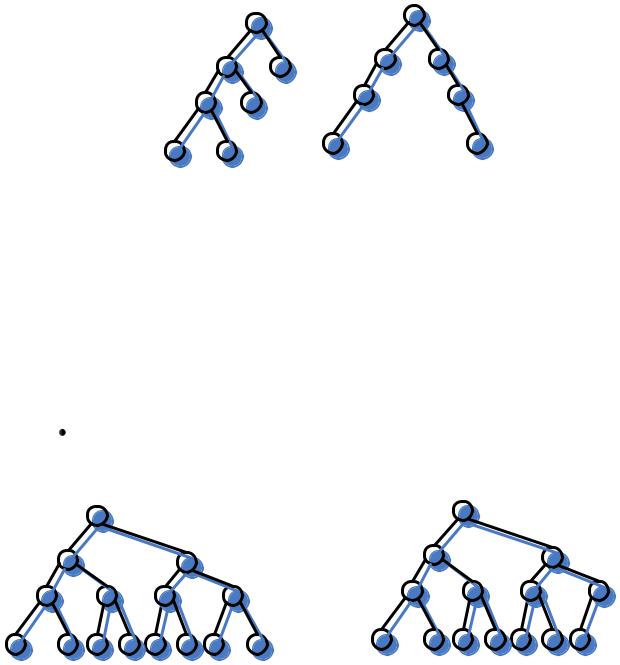
Рис.2. Раздваивающееся и не раздваивающееся деревья

1.2. Полное бинарное дерево.

Определение 1. Полное дерево – это раздваивающееся дерево, все листья которого находятся на одном уровне.

Определение 2. Бинарное дерево Т называется полным деревом, если:

оно пустое дерево

либо оба его поддерева имеют одинаковую высоту, и оба являются полными.

Рис. 3.Полное и неполное деревья

Для полных деревьев можно по количеству узлов рассчитать высоту и по высоте определить количество узлов.

Пример 3. Определения высоты дерева по количеству узлов в полном дереве.

Пусть, полное бинарное дерево, представленное на рис. 3 имеет 15 узлов. На каждом i-ом уровне располагается 2i узлов, тогда: на нулевом

уровне 20, на первом уровне 21, на втором 22, на третьем 23, всего 15 узлов, т.е. высота дерева равна максимальному уровню, т.е. 3.

Пример 4. Определение количества узлов полного бинарного дерева по его высоте.

Пусть дерево имеет высоту 3. Тогда количество его узлов будет равно сумме членов геометрической прогрессии: 1+21+22+23 т.е. вычисляется по формуле

нашем примере n=4, b1, это первый член прогрессии, q – шаг геометрической последовательности, в примере q=2. Следовательно количество узлов в дереве равно 15.

1.3.Законченное бинарное дерево.

Это полное дерево до уровня Heigh(Т)-1 (высота -1), а все листья на нижнем уровне располагаются ближе к левому краю дерева.

Рис. 4. Дерево 1 – законченное дерево, деревья 2 и 3 не являются законченными

Дерево 2 не является законченным деревом, так как оно неполное до уровня Heigh(Т)-1 (у узла С нет правого поддерева). Дерево 3, так же не является законченным, так как узлы K, N, J, O не являются максимально приближенными к левому краю дерева.

Узлам законченного дерева можно присвоить индексы. Корневой узел будет иметь индекс 0, тогда для любого узла с индексом i, который имеет дочерние узлы индекс левого дочернего вычисляется по формуле 2i+1, а правого 2i+2.

Рис.5. Индексированное законченное дерево Так как узлы дерева можно индексировать, то его можно хранить в

одномерном массиве.

Например, дерево 1 с рисунка 4, можно представить массивом

9. Идеально сбалансированное бинарное дерево

Бинарное дерево называется идеально сбалансированным, если для каждой его вершины количество вершин в левом и правом поддереве различаются не более чем на 1.

Пусть требуется построить бинарное дерево с n узлами и минимальной высотой (максимально "ветвистое" и "низкое"). Такие деревья имеют большое практическое значение, так как их использование сокращает машинное время, требуемое на выполнение различных алгоритмов.

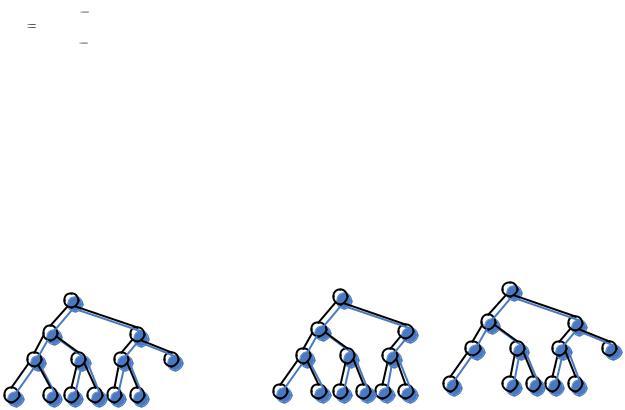
Рис.6. Примеры идеально сбалансированных бинарных деревьев

Алгоритм построения идеально сбалансированного дерева при известном числе вершин n лучше всего формулируется с помощью рекурсии. При этом необходимо лишь учесть, что для достижения минимальной

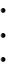
высоты при заданном числе вершин, нужно располагать максимально возможное число вершин на всех уровнях, кроме самого нижнего. Это можно сделать очень просто, если распределять все поступающие в дерево вершины поровну слева и справа от каждой вершины.

Суть алгоритма

взять одну вершину в качестве корня.

построить левое поддерево с nl = n DIV 2 вершинами тем же способом. построить правое поддерево с nr = n-nl-1 вершинами тем же способом.

Реализация алгоритма создания бинарного сбалансированного дерева приведена в примере

#include "stdafx.h" #include "iostream" using namespace std; class Bin

{

private:

struct Node

{int data; Node *left;

Node *right;

};

typedef Node *Tree; Tree Root;

int n;

public:

Bin(int n1);

void createtree(Tree &T,int n); void out(Tree &T,int i);

void print();

const static int l=5;

};

Bin::Bin(int n1)

{

n=n1; Root=0;

createtree(Root,n);

}

void Bin::createtree(Tree &T,int n) {int nl,nr,x;

if (n!=0)

{

T=new Node;

T->left=0;

T->right=0; cin>>x; T->data=x;

nl=n/2; nr=n-nl-1;

Bin::createtree(T->left,nl); Bin::createtree(T->right,nr);

}

}

struct TNode

{int data; TNode *left; TNode *right;

};

void Bin::out(Tree &T,int i)

{

if(T)

{

out(T->left,i+1);

for (int k=0; k<l*i;k++) cout<<' ';

cout<<T->data<<endl; out(T->right,i+1);

}

}

void Bin::print()

{

out(Root,0);

}

int main()

{Bin B(7); B.print();

cin.get(); return 0;

}

10. Бинарное дерево выражений

Выражение, содержащее бинарные операции можно представить как бинарное дерево, в котором внутренние узлы будут хранить операции, а листья операнды.

Например, выражение (a+b)*(c-d/e) можно представить дерево Т, в корневом узле которого будет находиться операция *, правое поддерево будет представлять правый операнд (правая скобка), а левое поддерево – правый операнд (левая скобка).

Рис.7. Дерево выражения (a+b)*(c-d/e)

Если операнды – числа, то дерево можно использовать для вычисления значения выражения.

Если операнды - переменные, то в узел операнда записывается ссылка на ячейки переменных.

Дерево выражений можно использовать при вычислении значения выражения. При этом необходимо учитывать приоритетность операций и правило: сначала надо вычислить значение выражения левого поддерева, затем правого, а затем выполнить операцию, находящуюся в корне.

Алгоритмы обхода бинарного дерева

Обход дерева – это алгоритм, который позволяет осуществить доступ ко всем узлам дерева, только один раз. Над данными узла можно выполнять операции.

Обход формирует список пройденных узлов.

Алгоритмы обхода методом в “глубину”

Обход в прямом порядке бинарного дерева

посетить корневой узел

обойти в прямом порядке левое поддерево обойти в прямом порядке правое поддерево

Примечание. В алгоритмах обхода используется процедурный параметр, который определяет алгоритм обработки значения узла дерева T- visit.

void Pereorder (BinTree T){ if (! Empty(T)){

Visit(Root(T));

Pereorder(LeftTree(T),visit);

Pereorder(RightTree(T),visit);

}

}

Обход бинарного дерева в симметричном порядке

обойти в симметричном порядке левое поддерево

посетить корневой узел обойти в симметричном порядке правое поддерево