3-й семестр / Лекция 4 - B-дерево

Тема B – дерево

Структура данных, которая используется для поиска данных в структурах данных размещенных во внешних структурах данных – файлах и базах данных.

С точки зрения внешнего логического представления B-дерево - это сбалансированное сильно ветвистое дерево во внешней памяти. Сбалансированность означает, что длина пути от корня дерева к любому его листу одна и та же. Ветвистость дерева - это свойство каждого узла дерева ссылаться на большое число узлов-потомков. С

точки зрения физической организации B-дерево представляется как мультисписочная структура страниц внешней памяти, т.е. каждому узлу дерева соответствует блок внешней памяти (страница). Внутренние и листовые узлы обычно имеют разную структуру -

состоят из нескольких элементов.

Поиск в B-дереве - это прохождение от корня к листу в соответствии с заданным значением ключа. Заметим, что поскольку деревья сильно ветвистые и сбалансированные,

то для выполнения поиска по любому значению ключа потребуется одно и то же (и

обычно небольшое) число обменов с внешней памятью. Более точно, в сбалансированном дереве, где длины всех путей от корня к листу одни и те же, если во внутренней странице помещается n ключей, то при хранении m записей требуется дерево глубиной logn(m), где logn вычисляет логарифм по основанию n. Если n достаточно велико (обычный случай), то глубина дерева невелика, и производится быстрый поиск.

Основной "изюминкой" B-деревьев является автоматическое поддержание свойства сбалансированности.

Не листовые узлы В- дерева содержат ссылки на узлы – потомки, а листовые узлы содержат ссылки на записи файла с соответствующим ключом.

3.1. Структура В – дерева.

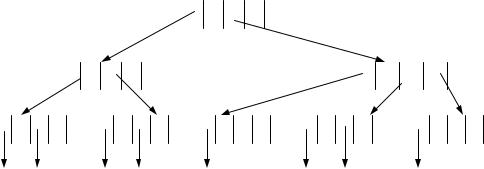
Листовые узлы и внутренние узлы В – дерева имеют различную структуру. Каждое В – дерево имеет константу, которая определяет количество элементов, содержащихся в одном узле. Рассмотрим пример В – дерева с константой 3, т.е. узел содержит максимально три элемента.

Пусть дерево содержит ключи записей файла, ключи выбираются из последовательно читаемых записей и помещаются в дерево. Список прочитанных ключей:

31, 3, 18, 35, 29, 1, 33.

Рис. 1. В – дерево с ключами записей файла

3.2. Правила создания В-дерева

В дерево это n-арное сбалансированное дерево поиска. Каждый внутренний узел имеет структуру

где pi – ссылка на i – ого сына узла (0≤i≤n) ki – ключ записи в файле (0≤i≤n)

Пара ( pi,ki) – элемент узла

1)Корень, являющийся листом имеет по крайней мере двух сыновей.

2)Каждый внутренний узел имеет от [n/2] до n сыновей. Где [n/2] – округление до ближайшего целого.

3)Все пути от корня до листа имеют одинаковую длину.

4)Все ключи упорядочены по возрастанию: k1<k2<k3…….<kn

5)Все ключи в поддереве на которое указывает p0 строго меньше ключа k1.

6)Для 2≤i≤n-1 все ключи в поддереве на которое указывает pi, имеют значения большие или равные ki-1 и меньшее ki.

7)Все ключи в поддереве, на которое указывает pn, больше или равны kn-1. Т.о. для i>1 ключ ki-1 всегда минимальный ключ в поддереве, на которое указывает pi.

8)Листовой узел содержит от [n/2] до n-1 указателей на записи файла.

3.3.Операции в В – дереве

3.3.1. Поиск записи файла с заданным ключом Пусть key заданный ключ поиска

1. Ключ key сравнивается со значениями ключей корневого узла. Если ki≤key≤ki+1, то происходит переход к поддереву, на которое указывает pi и процесс повторяется.

2.Если key<k1, то далее поиск происходит в поддереве по ссылке p0, если key≥kn, то поиск ключа осуществляется в поддереве по ссылке pn.

3.Пункты 1 и 2 повторяются, пока процесс не спуститься к листу. В списке листов

поиск осуществляется с помощью алгоритма линейного или бинарного поиска.

Задание для самоконтроля. Проверьте алгоритм поиска для записи с ключом 29.

3.3.2. Вставка записи с ключом key в файл

Рассмотрим в общем виде выполнение операции добавления новой записи в файл,

доступ к записям которого осуществляется посредством В – дерева.

Вставляем запись в файл и запоминаем адрес ее размещения

Ищем в В – дереве лист (далее, найденный, разделенный), в котором должен разместиться ключ вставляемой записи. Если в найденном листовом узле есть свободное место, то вставляем ключ в этот лист и упорядочиваем все ключи листа по возрастанию. Если листовой узел заполнен, то выполняется его разбиение на два листа, следующим образом:

создается новый узел, и все ключи найденного узла и ключ вставленной записи упорядочиваются по возрастанию;

первые [n/2] ключей помещаются в левый лист (найденный ) и остальные в правый лист (новый).

После этого (листов стало больше) корректируются ключи и указатели в узлах,

которые составляют путь к разделенному листу.

Пример 1.Вставки записей в файл и создание для него В – дерева.

Воспользуемся ключами, представленными в В- дереве рисунка 1 и рассмотрим процесс создания В – дерева.

И так, пусть создается файл и в него последовательно вставляются записи с ключами: 31, 3, 18, 35, 29, 1, 33.

1)Вставляем запись с ключом 31 в файл и запоминаем адрес(ссылку) по которому размещена запись на диске.

2)Вставляем ключ 33 в В – дерево.

Так как дерево еще пусто, то создается первый узел – лист, который сейчас является корнем дерева, и в него вставляется ключ 31, в поле p0 записываем ссылку на запись с ключом 31 в файле. На рис.2 вид (1) изображено В – дерево из одного листового узла с ключом 31.

3) Вставляем запись с ключом 3 в файл, и ключ 3 в В – дерево. Так как дерево не пусто, и, оно имеет один лист, в котором есть свободное место для ключа, то вставляем

ключ и ссылку на запись с этим ключом в этот лист, предварительно упорядочив элементы узла по возрастанию ключей. Полученное дерево представлено на рис.2(2).

4) Вставляем запись с ключом 18 в файл, и ключ 18 в В – дерево. В дереве только одна листовая запись, которая имеет n-1 указатель на записи файла, согласно правил В – дерева – листовая запись заполнена, тогда производим деление листовой записи на две:

упорядочиваем ключи 3, 31, 18 по возрастанию, т.е. получаем последовательность 3, 18, 31

добавляем новый узел в В – дерево

первые [n/2] (так как n=3 примере, то n/2 с округлением даст 2) ключей записываются в левый лист (это 1 и 18), а остальные (это 31) в новый (правый)

узел.

Так как в дереве уже более одного листа, то создаем внутренний узел верхнего уровня - корень дерева, в который помещается ключ 31, согласно правила внутреннего узла (ссылка р1 должна ссылаться на узел с ключами ,большими

либо равными ключу к1). Получаем дерево представленное на рис.2(3).

5) Вставляем запись с ключом 35 в файл, и ключ 35 в В – дерево. Ключ 35 должен разместиться в листе, где находится ключ 31, в этом узле есть свободное место, то 35

вставляем в этот лист и упорядочиваем элементы записи согласно ключей. Получаем дерево, представленное на рис.2(4).

6)Вставляем запись с ключом 29 файл, и ключ 29 в В – дерево. Ищем лист, в

который надо вставить ключ 29, т.к. 29<31, то его надо вставить в левый лист, где находится 3 и 18, но он заполнен, поэтому производи деление листа и согласно упорядочения ключ 29 разместиться в правом листе. Т.к. в дереве уже три листа, то надо вставлять ключ в корневой узел согласно правилу. В результате получим дерево рис.2(5).

7)Вставляем запись с ключом 1 в файл, и ключ 1 в В – дерево. Ищем лист, в

который надо вставить ключ 1, т.к. 1<29, то его надо вставить в левый лист, где находится

3 и 18, но он заполнен, поэтому производи деление листа и согласно упорядочения ключи

1 и 3 разместятся в левом листе, а ключ 18 в правом. Т.к. в дереве уже четыре листа, а

каждый внутренний узел может содержать от [n/2] до n указателей на узлы нижнего уровня, то ключ 18 надо вставлять в корень. В корневом узле нет места для третьего ключа (вспомним, что в нашем примере n=3, а, следовательно, может быть только два ключа и три ссылки) поэтому разделяем внутренний узел (корень) на два внутренних узла. На два внутренних узла надо создавать один верхнего уровня и перемещать в него такой из ключей разделяемого узла, чтобы выполнялось правило 3 В – дерева. В

результате получиться дерево рис.2(6).

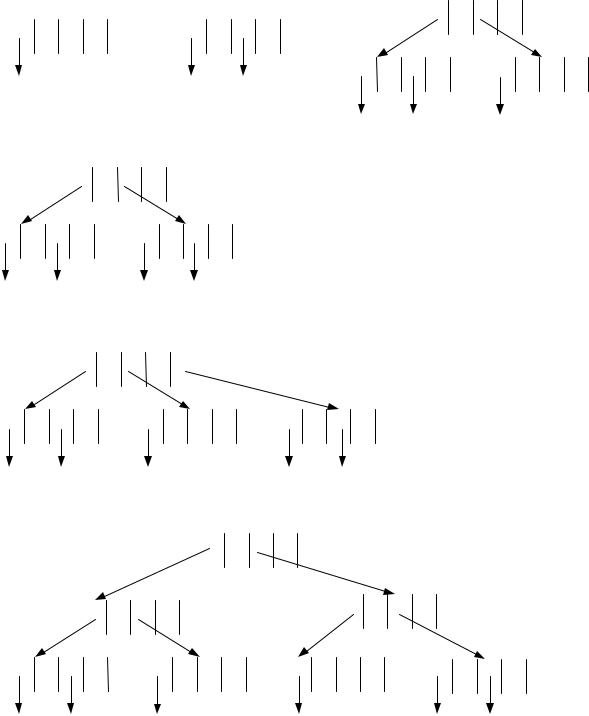
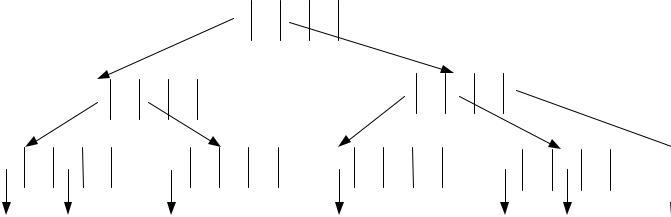
8) Вставляем запись с ключом 33 в файл, и ключ 33 в В – дерево. Ключ должен быть вставлен в самый правый лист дерева, так как 33>31. Но он заполнен, тогда делим правый лист на два, упорядочиваем элементы листовых узлов. Корректируем корневой узел разделенного узла, вставляя в него клюс 35 и ссылку на новый лист. Получаем дерево на рис2.(7).

Файл с записями

(6)

Рис.2. Процесс создания В – дерева

Задание для самоконтроля. Обойдите дерево с целью поиска записи с ключом 33.

3.3.3. Удаление записей из файла Операция удаления сводиться к поиску записи в файле по В – дереву,

удалению записи из файла и возможно перестройке В – дерева.

Пример. Удаление записей из файла и перестройка В – дерева

1)Удалим из файла, В – дерево которого представленного на рис.2(7),

запись с ключом 33. Так как этот ключ находится в листе и кроме него в узле находится еще ключ (лист может содержать минимум [n-1/2]

ключ), то перестройка дерева не требуется. Просто запись удаляется из

файла, а ключ из листа.

2)Удалим из файла запись с ключом 18. Находим лист с ключом 18. Этот лист содержит только один ключ 18, мы его исключаем из узла и узел становится пустым, а, следовательно, его надо удалять. Но тогда в родительской записи будет одна ссылка, что нарушает правило 2 В – дерева. Если количество ссылок у родительского узла (назовем его Р)

на внутренние узлы нижнего уровня (на сыновей) меньше чем n/2, то проверяются узлы находящиеся слева или справа от родительского узла (назовем его Р1). Если правый или левый узел Р1 имеют по

крайней мере [n/2]+2 сыновей, то узлы и ссылки распределяются поровну между родителем Р и его правым или левым братом Р1, так чтобы они имели по [n/2] сыновей. Затем надо изменить значения ключей в родителях перестроенных узлов Р и Р1. Этот процесс может быть рекурсивно распространен на родителей узлов Р и Р1.