
4 Расчёт подвески
Построение упругой характеристики и определение основных
параметров подвески
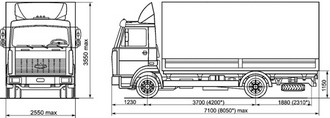
Рисунок 4.1 – Габаритные размеры прототипа
Нагрузка на заднюю ось:
- в снаряженном состоянии – 2950 кг
- в груженом состоянии – 6350 кг
Основываясь на проведенном обзоре существующих подвесок и технической характеристике прототипа, предлагаю применить на проектируемом автомобиле подвеску, состоящую из малолистовой рессоры с подрессорником.
Задаемся частотой собственных колебаний подрессоренной массы автомобиля
![]() Гц=12,56
рад/с.
Гц=12,56
рад/с.
Определяем статический прогиб рессоры в снаряженном состоянии:
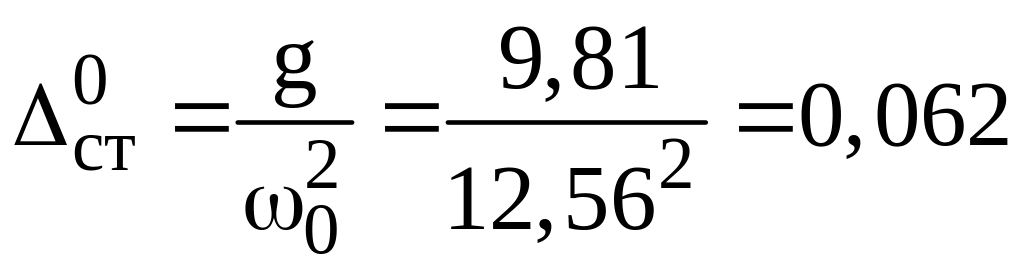 м.
м.
Определим нагрузку, приходящуюся на подвеску от подрессоренной массы в снаряженном состоянии:
![]() Н.
Н.
Откладываем
на упругой характеристике (рисунок 3.1)
значения
![]() и
и
![]() - точка А. Точка О – начало координат.
Проводим линию ОА. На продолжении линии
ОА отмечаем точку включения подрессорника
В. Ордината этой точки определяется:
- точка А. Точка О – начало координат.
Проводим линию ОА. На продолжении линии
ОА отмечаем точку включения подрессорника
В. Ордината этой точки определяется:
![]() ,
,
где α=0,3...0,5 – коэффициент, показывающий долю нагрузки при которой включается подрессорник, принимаем α=0,4;
![]() ,
,
где Мг=6350 кг – нагрузка на ось в груженом состоянии;
Мсн=2950 кг – нагрузка на ось в снаряженном состоянии;
![]() Н;
Н;
![]() Н.
Н.
Жесткость основных рессор определяется:
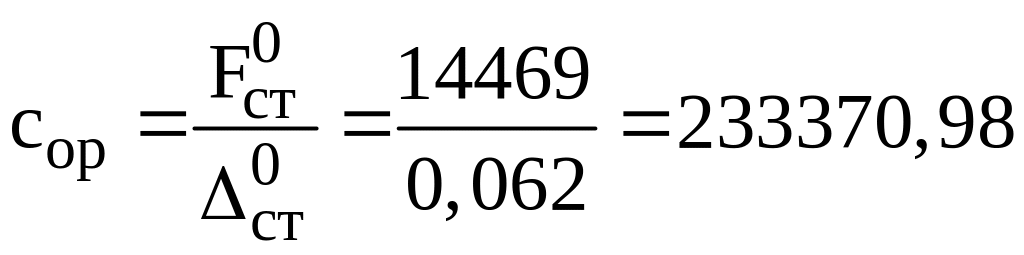 Н/м.
Н/м.
Прогиб рессоры до включения подрессорника (абсцисса точки В):
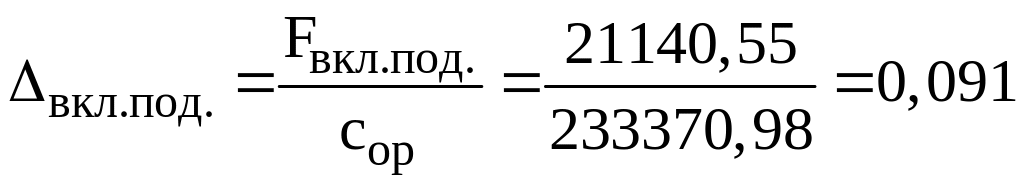 м.
м.
Задаемся частотой собственных колебаний после включения подрессорника
![]() Гц=11,304
рад/с.
Гц=11,304
рад/с.
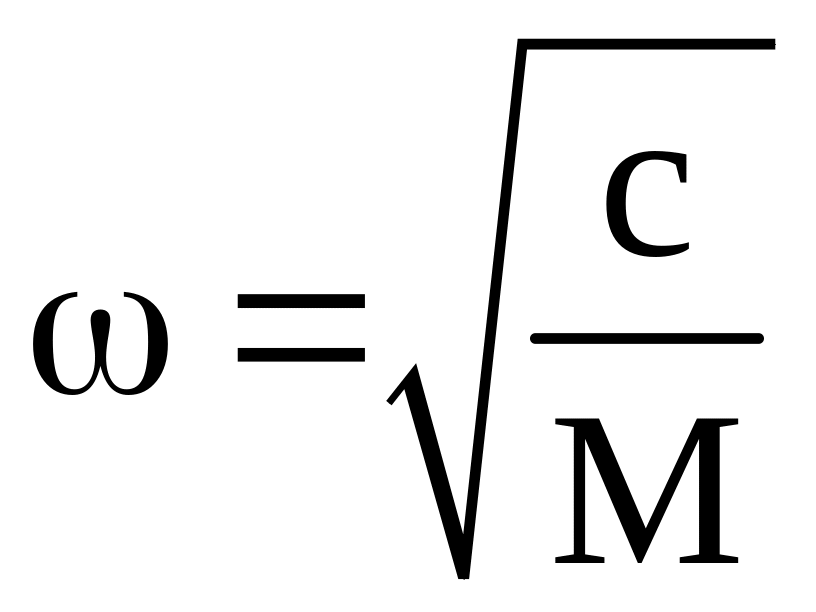
Тогда жесткость рессоры:
![]() Н/м.
Н/м.
![]()
Статическая нагрузка груженого автомобиля на подвеску (ордината точки С):
![]() H;
H;
![]() Н;
Н;
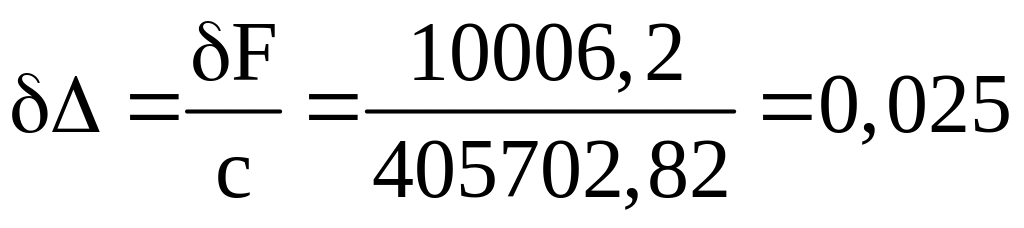 м.
м.
Тогда статический ход подвески (абсцисса точки С):
![]() м.
м.
Зададимся коэффициентом динамичности kд=1,8. Определим максимальную нагрузку на подвеску (точка D):
![]() Н.
Н.
Определим полный прогиб подвески:
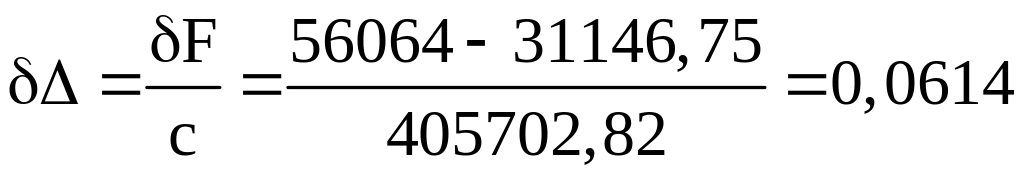 м;
м;
![]() м.
м.
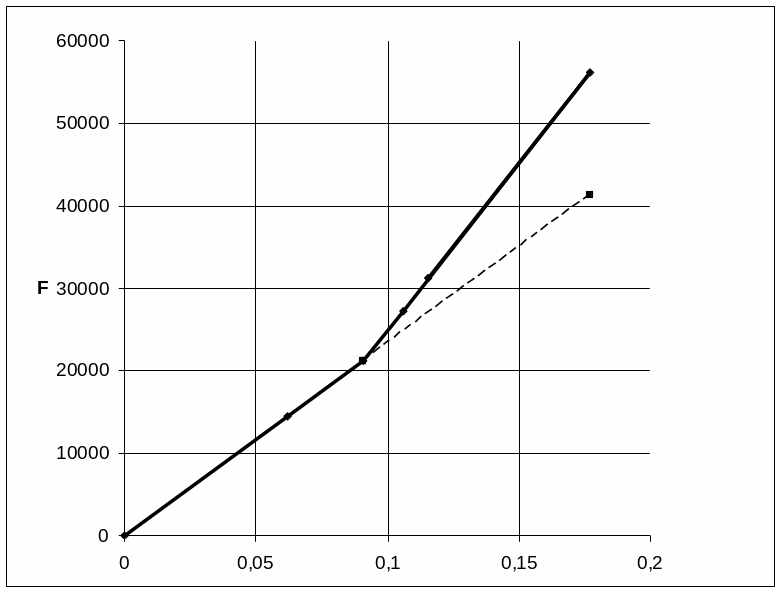
Рисунок 4.2 – Упругая характеристика рессорной подвески
Расчет рессоры
По конструктивным параметрам задаемся расстоянием между стремянками: lст=95 мм.
Длина рессоры определяется:
![]() ,
,
где Lа – активная длина рессоры, вычисляется из формулы:
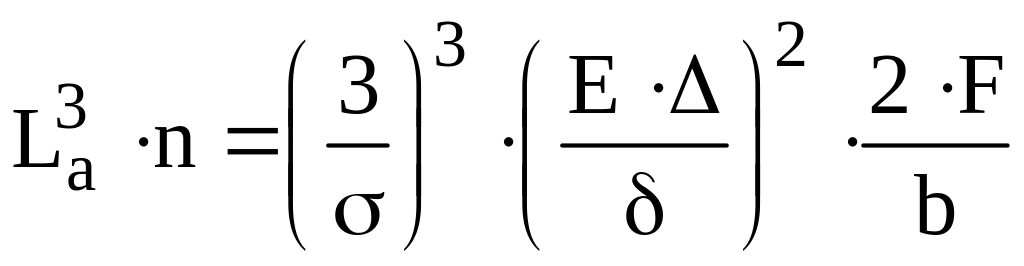 ;
;
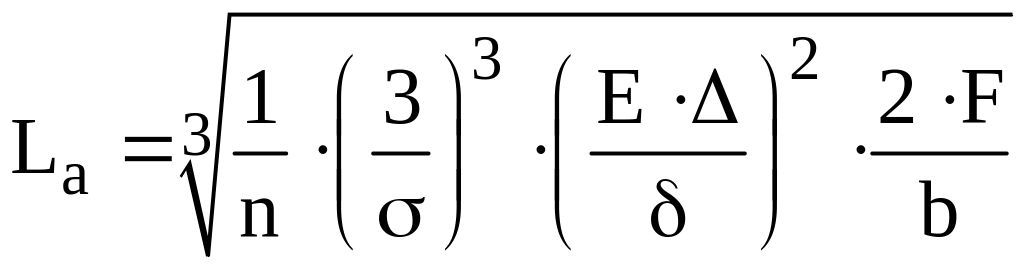 ,
,
где n – количество листов рессоры, принимаем n=4;
σ=950 МПа – допустимое напряжение в рессоре при полном прогибе;
E=2·105 МПа – модуль Юнга;
∆=0,18 м – максимальный прогиб рессоры (из упругой характеристики подвески);
δ=1,5 – коэффициент, учитывающий отличие рессоры от идеальной;
F=41170,6 Н – максимальная нагрузка на рессору (из упругой характеристики);
b – ширина листа рессоры, по конструктивным соображениям принимаем b=0,12 м.
Получаем:
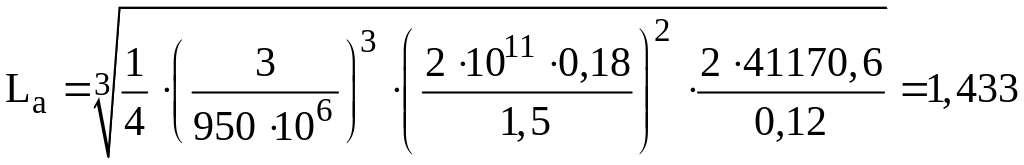 м.
м.![]()
Принимаем минимальную толщину конца листа рессоры h=10 мм.
Определим максимальную толщину листа рессоры:
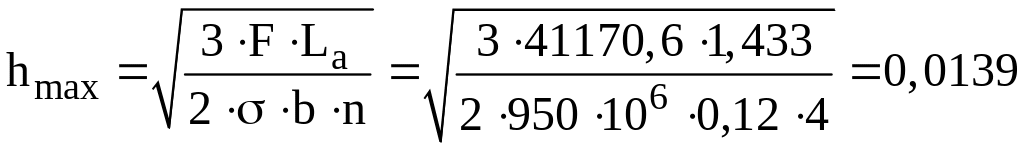 м.
м.
Далее с помощью специальной программы на ЭВМ производим оптимизацию полученных параметров рессоры.
Таблица 4.1 – Результаты оптимизации рессоры
Исходные данные |
Результаты |
||
Статическая нагрузка |
26879,5 Н |
Масса активной части листов |
53,137 кг |
Статическое напряжение |
612,2 МПа |
Максимальная толщина листа |
15,324 мм |
Статический прогиб |
116 мм |
Уточненный статический прогиб |
115,324 мм |
Толщина конца листа |
10 мм |
Количество листов |
4 |
Диапазон ширины листа |
100…120 мм |
Ширина листа |
100 мм |
Диапазон длины листа |
1200…1600 мм |
Активная длина листа |
1440 мм |
Диапазон количества листов |
3…5 |
|
|
Далее произведем расчет параметров подрессорника.
Активная длина подрессорника:
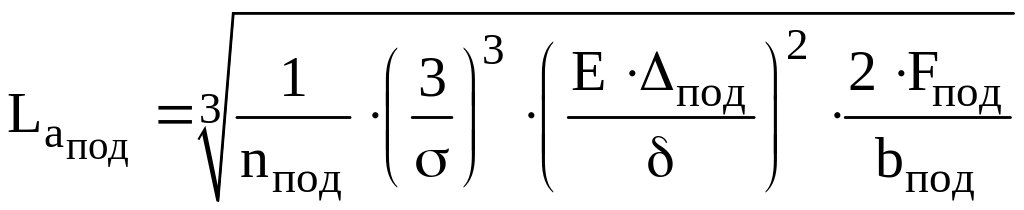
где nпод – количество листов рессоры, принимаем nпод=1;
∆под=0,09 м – максимальный прогиб подрессорника (из упругой характеристики подвески);
Fпод=14893,54 Н – максимальная нагрузка на подрессорник (из упругой характеристики);
bпод – ширина листа подрессорника, по конструктивным соображениям принимаем b=0,12 м.
Получаем:
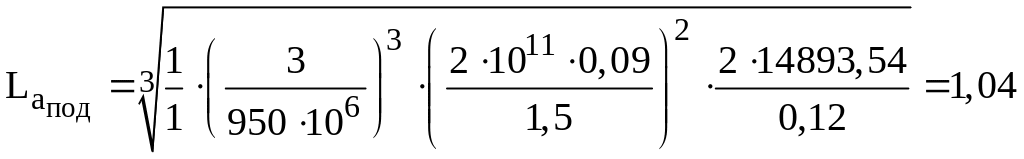 м.
м.
Принимаем минимальную толщину конца листа рессоры h=10 мм.
Определим максимальную толщину листа подрессорника:
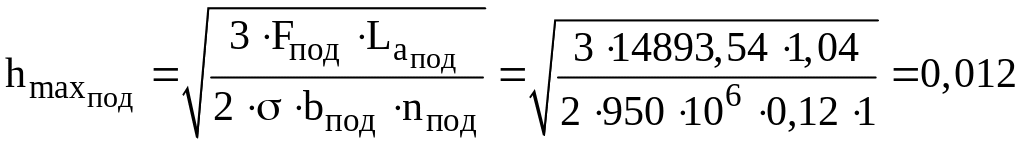 м.
м.
Далее с помощью специальной программы на ЭВМ производим оптимизацию полученных параметров подрессорника.
Таблица 4.2 – Результаты оптимизации подрессорника
Исходные данные |
Результаты |
||
Статическая нагрузка |
4267,25 Н |
Масса активной части листов |
6,522 кг |
Статическое напряжение |
274,4 МПа |
Максимальная толщина листа |
13,7 мм |
Статический прогиб |
26 мм |
Уточненный статический прогиб |
26 мм |
Толщина конца листа |
10 мм |
Количество листов |
1 |
Диапазон ширины листа |
100…100 мм |
Ширина листа |
100 мм |
Диапазон длины листа |
700…1200 мм |
Активная длина листа |
873 мм |
Диапазон количества листов |
1…1 |
|
|
Принимаем параметры рессоры и подрессорника, полученные в результате оптимизации.
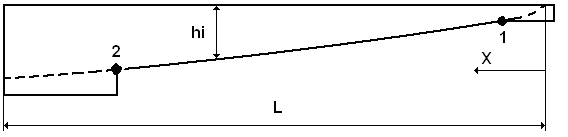
Рисунок 4.3 - Расчетная схема для профилирования листов рессоры и подрессорника
Производим профилирование листов рессоры и подрессорника.
![]() мм;
мм;
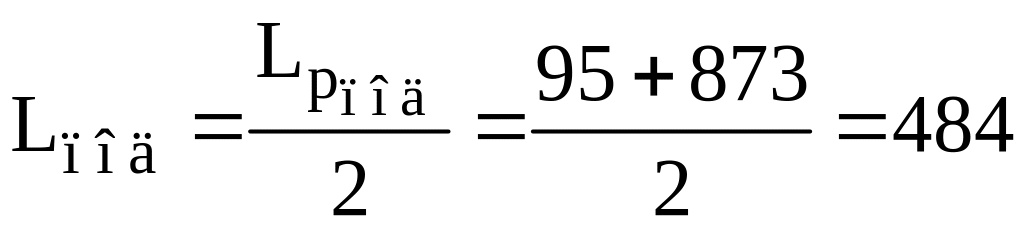 мм;
мм;
 .
.
Таблица 4.3 – Результаты профилирования листов рессоры и подрессорника
Профилирование листа рессоры |
|||||||||||
Хi, мм |
0 |
76,75 |
153,5 |
230,25 |
307 |
383,75 |
460,5 |
537,25 |
614 |
690,75 |
767,5 |
hi, мм |
0 |
4,85 |
6,85 |
8,39 |
9,69 |
10,84 |
11,87 |
12,82 |
13,71 |
14,54 |
15,324 |
Профилирование листа подрессорника |
|||||||||||
Хi, мм |
0 |
48,4 |
96,8 |
145,2 |
193,6 |
242 |
290,4 |
338,8 |
387,2 |
435,6 |
484 |
hi, мм |
0 |
4,33 |
6,13 |
7,50 |
8,66 |
9,69 |
10,61 |
11,46 |
12,25 |
13,0 |
13,7 |
Расчет амортизатора
1 Расчет характеристики и параметров амортизатора
Для расчета амортизатора необходимо выбрать коэффициент апериодичности ψ=0,15…0,30. Принимаем ψ=0,25.
![]() .
.
Коэффициент сопротивления амортизатора:
![]() ,
,
где М=3175 кг – масса приходящаяся на подвеску, приведенная к центру колеса;
с =405702,82 Н/м – жесткость подвески, приведенная к центру колеса.
![]()
![]() .
.
Отношение коэффициентов сопротивления амортизатора на ходе отбоя и сжатия:
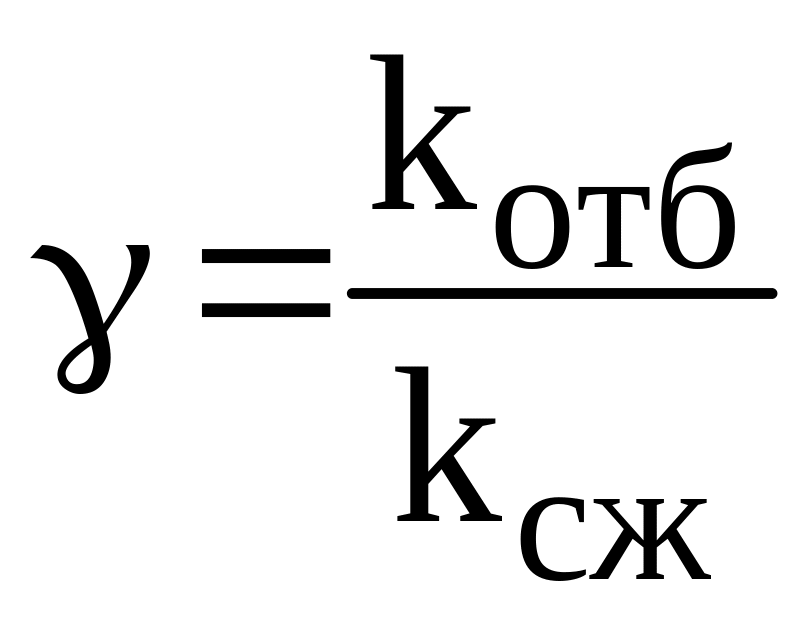 ;
;
γ=2…4. Принимаем γ=3.
![]() ;
;
 ;
;
![]() .
.
Характеристика амортизатора строится
в координатах
![]() .
Принимаем
.
Принимаем
![]() м/с.
Тогда
м/с.
Тогда
![]() Н;
Н;
![]() Н.
Н.
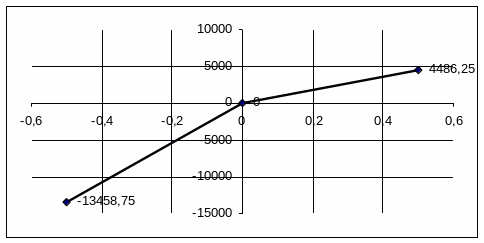
Рисунок 4.4 – Характеристика амортизатора
Площадь поршня:
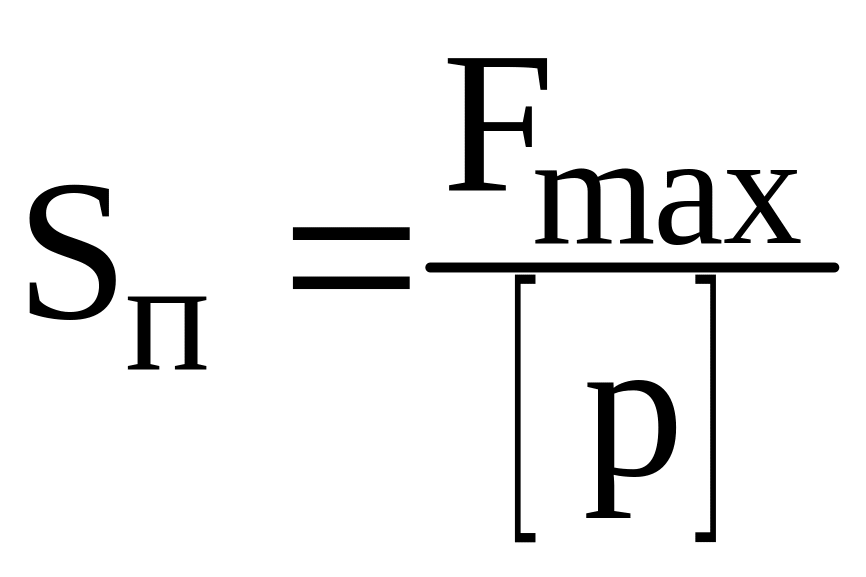 ,
,
где
![]() Н;
Н;
[p]=5…6 МПа – максимальное давление в амортизаторе. Принимаем
[p]=5 МПа.
![]() мм2;
мм2;
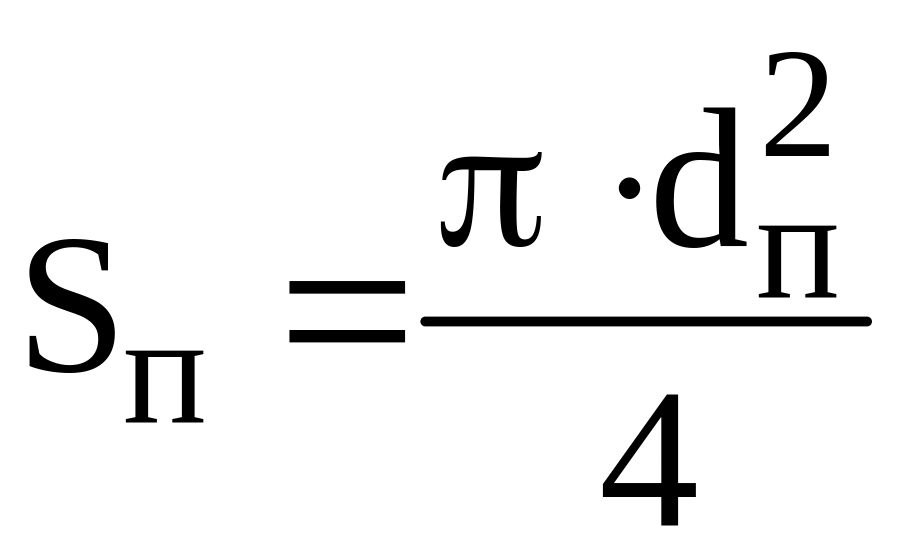 .
.
Диаметр поршня:
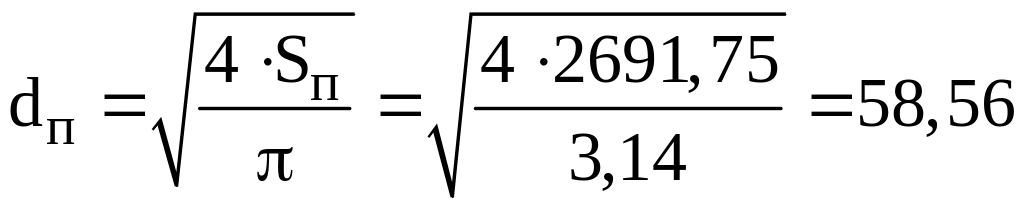 мм.
мм.
Принимаем dп=60 мм.
Принимаем длину штока из конструктивных соображений L=400 мм и определяем его диаметр, исходя из расчета стержня на устойчивость под действием сжимающей силы:
 ;
;
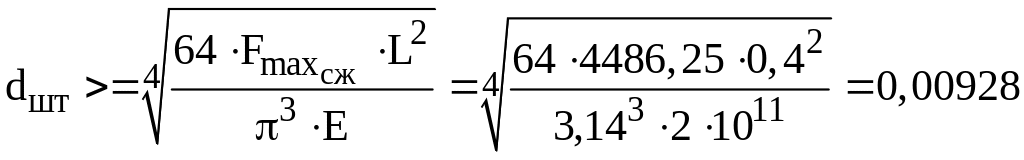 м.
м.
Полученный диаметр умножаем на коэффициент запаса продольной жесткости и получаем:
![]() мм.
мм.
Принимаем dшт=18 мм.
Площадь поршня на ходе сжатия:
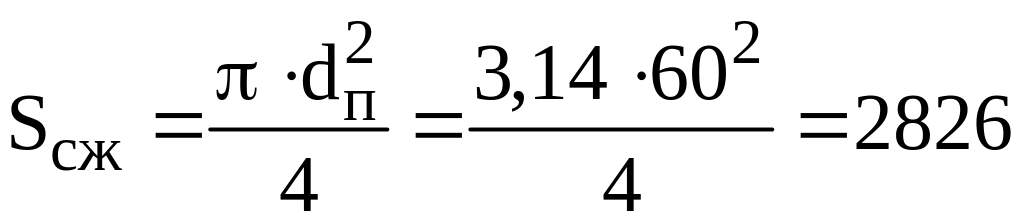 мм.
мм.
Площадь поршня на ходе отбоя:
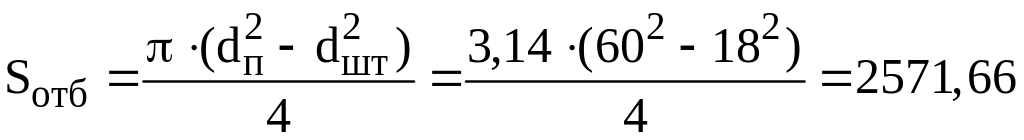 мм.
мм.
Принимаем диаметр кожуха dкож=90 мм.
2 Гидравлический расчет амортизатора
Расход жидкости
![]() ;
;
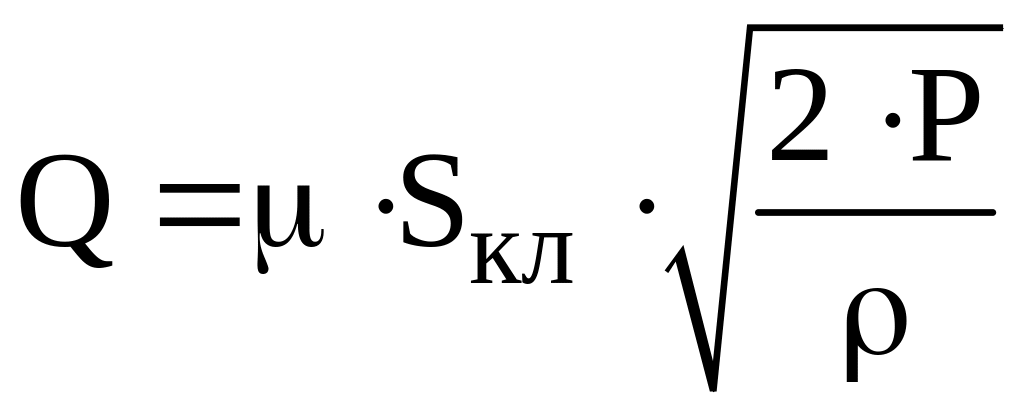 ,
,
где kу=0,97…0,98 – коэффициент утечек, принимаем kу=0,98;
μ=0,65…0,70 – коэффициент расхода, принимаем μ=0,70;
ρ=760 кг/м3 – плотность жидкости;
Sкл – площадь проходных сечений клапанов;
Sв – площадь вытеснителя (поршня).
Площадь проходных сечений клапанов на ходах сжатия и отбоя:
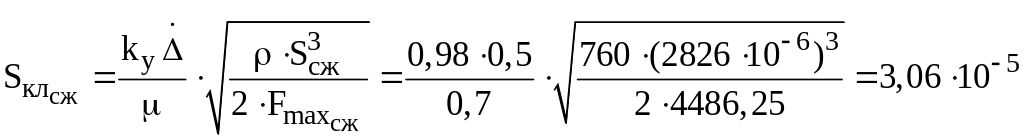 м2=30,6
мм2;
м2=30,6
мм2;
 м2=15,3мм2
м2=15,3мм2
3 Проверочный расчет амортизатора
Производится проверочный расчет на нагрев амортизатора.
Мощность, рассеиваемая амортизатором:
![]() ,
,
где kτ=45…60 Вт/м2 – коэффициент теплоотдачи, принимаем kτ=55 Вт/м2;
S – площадь рабочей поверхности амортизатора;
∆t – перепад температур между стенкой амортизатора и воздухом.
Мощность амортизатора:
![]() ,
,
где
![]() - средний коэффициент сопротивления
амортизатора.
- средний коэффициент сопротивления
амортизатора.
![]() ;
;
![]() м2;
м2;
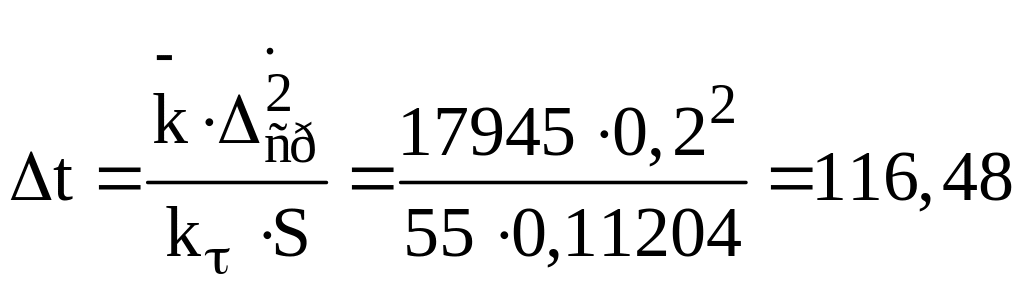 °С
°С![]() [120
°C].
[120
°C].
Прочностные расчеты
Произведем проверку на напряжение в листах рессоры при максимальной нагрузке:
![]() ,
,
где Fmax=41170,61 H – максимальная нагрузка, действующая на рессору (из упругой характеристики);
La=1440 мм - рабочая длина листов рессоры;
W – момент сопротивления изгибу поперечного сечения рессоры;
[σmax]=1000…1100 МПа – максимально допустимое напряжение в листах рессоры.
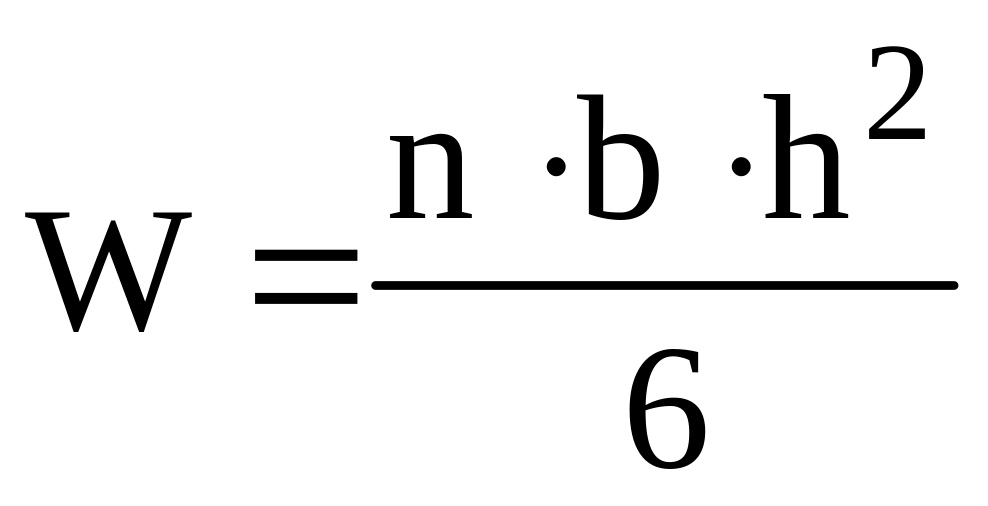 ,
,
где n=4 – количество листов рессоры;
h=15,324 мм – толщина листов рессоры;
b=100 мм – ширина листов рессоры.
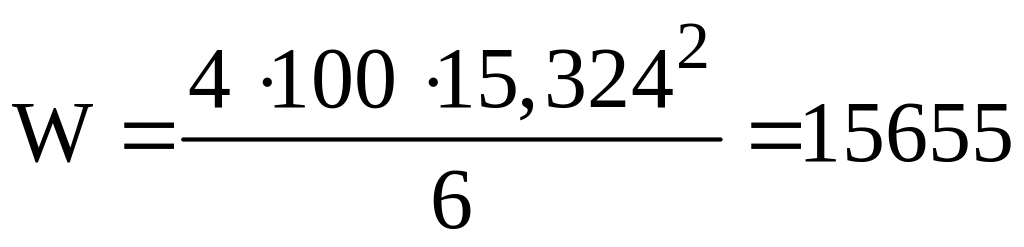 мм3;
мм3;
![]() МПа
<[1000] МПа.
МПа
<[1000] МПа.
Необходимое условие выполняется.
Аналогично произведем проверку на напряжение в подрессорнике при максимальной нагрузке:
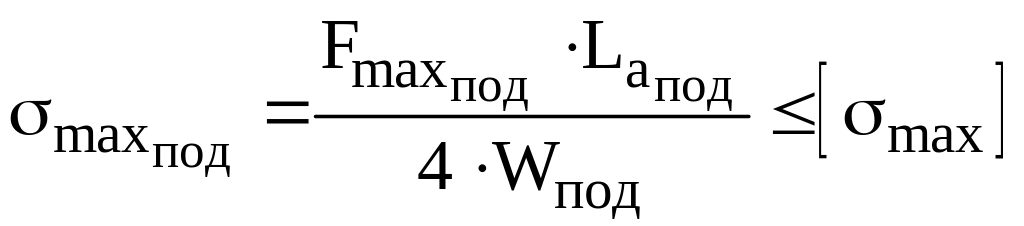 ,
,
где
![]() =14893,54
H – максимальная нагрузка,
действующая на подрессорник (из упругой
характеристики);
=14893,54
H – максимальная нагрузка,
действующая на подрессорник (из упругой
характеристики);
![]() =873
мм - рабочая длина листов рессоры;
=873
мм - рабочая длина листов рессоры;
nпод=1 – количество листов подрессорника;
hпод=13,7 мм – толщина листа подрессорника;
bпод=100 мм – ширина листа подрессорника.
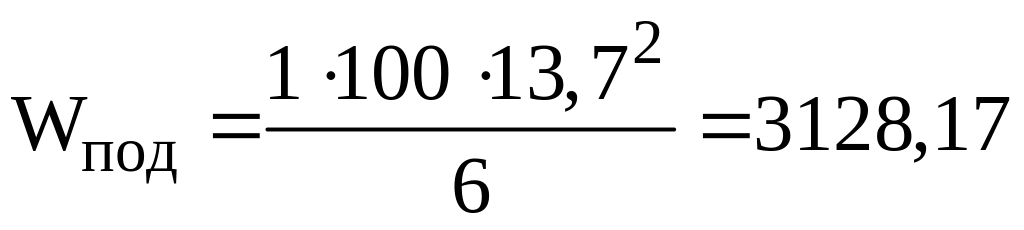 мм3;
мм3;
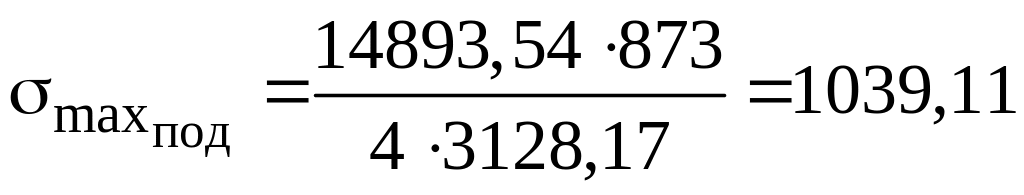 МПа.
МПа.
Необходимое условие выполняется.
