2.2 Расчет параметров упругих элементов

Целью расчета является определение основных параметров пружины и буферов и построение упругой характеристики подвески.

1) Рассчитаем максимальную статическую нагрузку, приходящуюся на одно переднее колесо:

где коэффициент сцепного веса: для переднеприводного полностью загруженного автомобиля .

2) Определим необходимую приведённую к колесу жесткость подвески:

где – угловая частота собственных колебаний подрессоренной части: рад/с.

3) Рассчитаем статический прогиб и динамический ход подвески:

где – ускорение силы тяжести: м/с².

4) Рассчитаем ход отбоя:

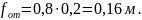
5) Определяем ход подвески, приходящийся на буфер сжатия и отбоя:

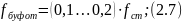
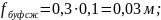
6) Рассчитываем энергоемкость подвески (максимальную динамическую нагрузку, воспринимаемую подвеской ):

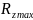где – коэффициент динамичности: для автомобилей ограниченной проходимости .

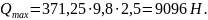
7) Рассчитаем жесткость шин:

Для начала определяем жесткость шин при внутреннем давлении :

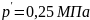где – поправочный коэффициент: для шин серии «70» .

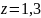Так как жесткость шин линейно зависит от их внутреннего давления, то для определения жесткости при рабочем давлении можно воспользоваться следующей формулой:

где – рабочее внутреннее давление: .

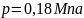8) Определим приведённую жесткость пружины:

Для последовательно соединённых упругих элементов результирующая жесткость будет рассчитываться по формуле:

Выразим из формулы (2.11) – приведённая жесткость пружины:

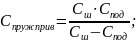
9) Определяем передаточное число по ходу:

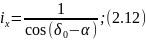
10) Рассчитаем передаточное число по силе направляющего аппарата подвески графоаналитическим способом:

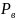Передаточное число по силе – это отношение силы на пружине к вертикальной силе на колесе. Для определения этого отношения воспользуемся теоремой о трех силах, из которой получается что при равновесии системы вертикальная сила , приложенная в центре контакта колеса с дорогой, сила действующая по оси нижнего рычага и сила от стойки должны пересекаться в одной точке (рис. 17), исходя из этого получим треугольник сил (рис. 18).

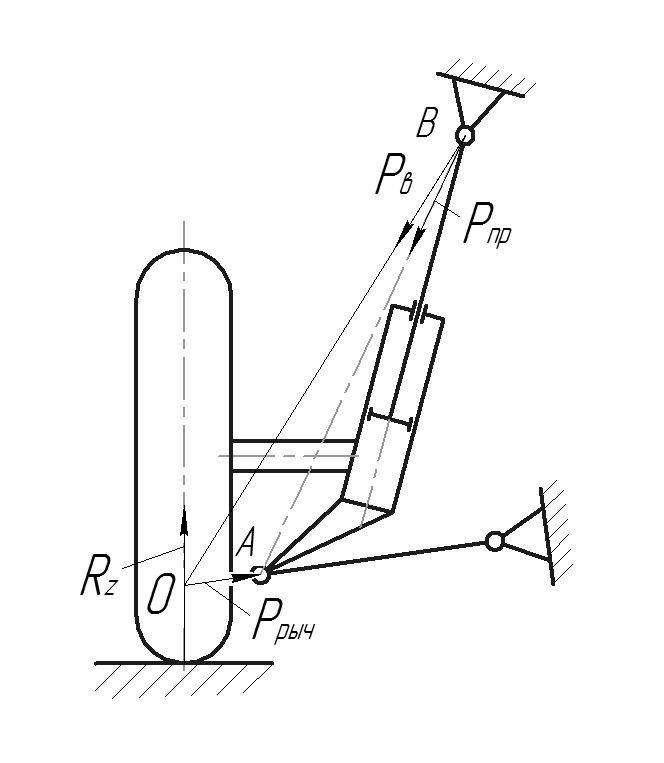
Рис. 17 Схема действия сил в статическом положении подвески

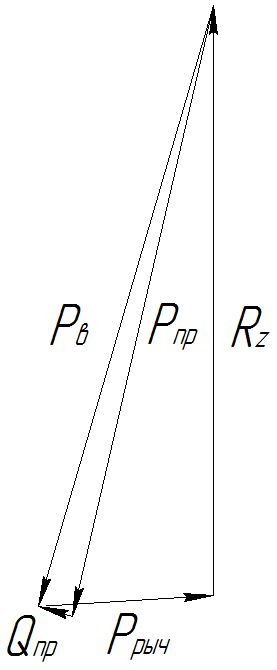
Рис. 18 Треугольник сил для статического положения подвески

Составляющая, направленная из центра верхней опоры и действующая на стойку, в свою очередь, может быть разложена на две составляющие силы: сила действующая вдоль оси пружины 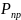, и, сила воспринимаемая штоком в направляющей и поршнем .

После построения треугольников, определим графическим способом отношение длины – длина вектора 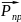к длине – длина вектора , которое и будет равно передаточному числу по силе.

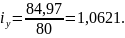
11) Определяем жесткость пружины:

12) Рассчитываем геометрические параметры пружины:

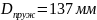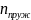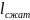К геометрическим параметрам пружины относится средний диаметр, который выбирается из соображений компоновки, принимаем , диаметр проволоки количество рабочих витков , полное количество витков , длина в сжатом состоянии , длина в свободном состоянии , шаг навивки и длина проволоки необходимая для изготовления пружины .

Выбираем для подвески пружину с нешлифованными и поджатыми на ¾ крайними витками.

12.1) Проверим условие прочности при статической и динамической нагрузке:

Расчет пружины ведется в случае действия максимальной статической нагрузки и максимальной динамической .

Так как при действии максимальной динамической нагрузки геометрия подвески значительно меняется, то ранее построенным треугольником сил (рис. 18) для определения передаточного числа по силе воспользоваться не получится, то построим новый треугольник сил, используя эту же методику построения. Обозначения сил соответствует обозначениям на рис. 18, отличие лишь в том, что у обозначении сил при действии максимальной динамической нагрузки в индексе прибавляется «max». Далее обозначения сил будут образовываться аналогичным образом, только за место «max» будет прибавляться соответствующее для рассматриваемого случая сокращение (Рис. 19).

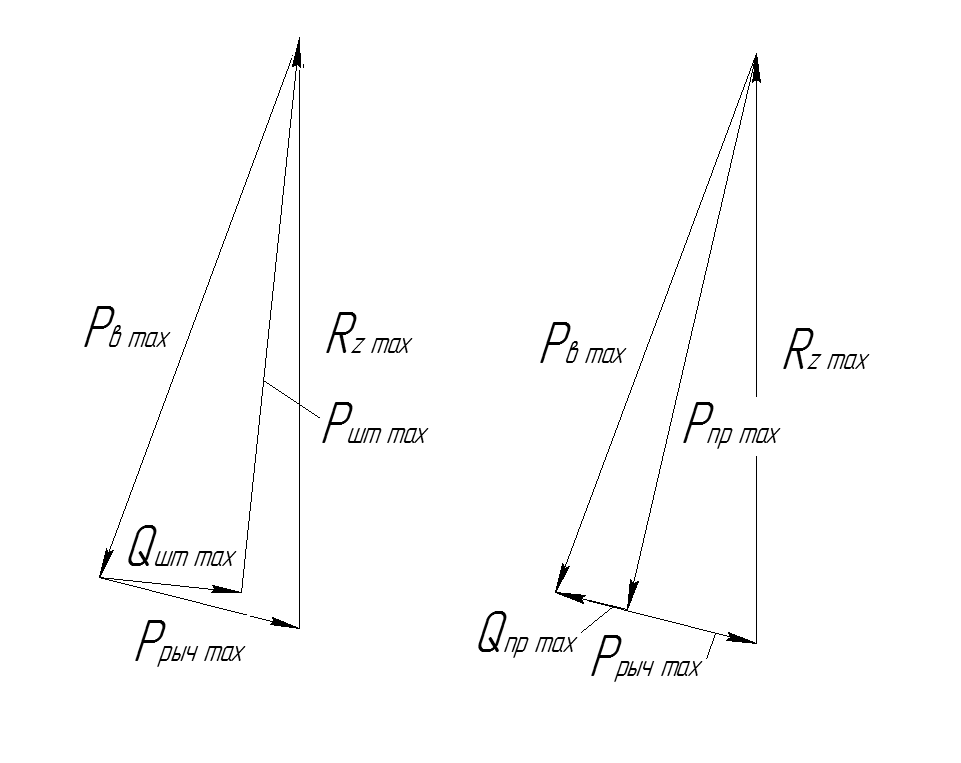
Рис. 19 Треугольник сил для максимальной динамической нагрузки

Передаточное число при действий максимальной динамической нагрузки рассчитывается по формуле (2.13):

Максимальная динамическая сила действующая на пружину рассчитывается по формуле:

Касательные напряжения в пружине определяются по формуле:

где – минимальный диаметр проволоки: о ; – коэффициент, учитывающий влияние кривизны витка, зависит от индекса пружины : для полученного индекса значение коэффициента определяем по рис. 2.123 [9], получаем .

Так как условие прочности выполняется, следовательно параметры: и подобраны правильно.

12.2) Определим число рабочих витков из условия обеспечения необходимой жесткости рассчитанной по формуле (2.14):

12.3) Определяем полное число витков пружины:

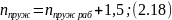
12.4) Для определения шага навивки, для начала определим гарантированный зазор между двумя витками, исключающий касание витков:

где – поправочный коэффициент, зависящий от индекса пружины: определяем по рис. 2.125 [9], получаем ; где – максимальный диаметр проволоки: .

12.5) Определяем длину пружины в полностью сжатом состоянии:

12.6) Определяем длину пружины в свободном состоянии:

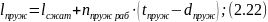
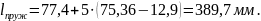
12.7) Определяем длину проволоки необходимую для изготовления пружины:

13) По результатам расчета строим упругую характеристику подвески:

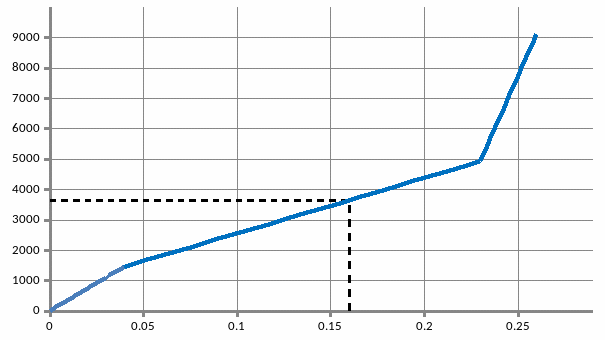
Рис. 20 Упругая характеристика подвески

На графике (рис. 20) указана точка соответствующая статическому положению.