5 Функциональный и прочностной расчёт передней подвески

5.1 Расчёт параметров гасящих элементов

Рассчитаем максимальную статическую нагрузку, приходящуюся на одно переднее колесо:

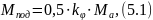
где коэффициент сцепного веса: для переднеприводного полностью загруженного автомобиля .

Определим необходимую приведённую к колесу жесткость подвески:

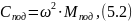
где – угловая частота собственных колебаний подрессоренной части: рад/с.

Рассчитаем статический прогиб и динамический ход подвески:

где – ускорение силы тяжести: м/с².

Рассчитаем ход отбоя:

Определяем ход подвески, приходящийся на буфер сжатия и отбоя:

Рассчитываем энергоемкость подвески (максимальную динамическую нагрузку, воспринимаемую подвеской ):

где – коэффициент динамичности: для автомобилей ограниченной проходимости .

Рассчитаем жесткость шин:

Для начала определяем жесткость шин при внутреннем давлении :

где – поправочный коэффициент: для шин серии «70» .

Так как жесткость шин линейно зависит от их внутреннего давления, то для определения жесткости при рабочем давлении можно воспользоваться следующей формулой:

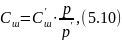
где – рабочее внутреннее давление: .

Определим приведённую жесткость пружины:

Для последовательно соединённых упругих элементов результирующая жесткость будет рассчитываться по формуле:

Выразим из формулы – приведённая жесткость пружины:

Определяем передаточное число по ходу:

Рассчитаем передаточное число по силе направляющего аппарата подвески графоаналитическим способом:

Рисунок 5.1 − Схема действия сил в статическом положении подвески

Определяем жесткость пружины:

Рассчитываем геометрические параметры пружины:

Передаточное число при действий максимальной динамической нагрузки рассчитывается по формуле:

Максимальная динамическая сила, действующая на пружину, рассчитывается по формуле:

Касательные напряжения в пружине определяются по формуле:

где – минимальный диаметр проволоки: ;

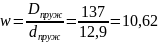– коэффициент, учитывающий влияние кривизны витка, зависит от индекса пружины : получаем .

Так как условие прочности выполняется, следовательно параметры: и подобраны правильно.

Определим число рабочих витков из условия обеспечения необходимой жесткости, рассчитанной по формуле:

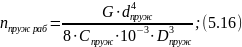
Определяем полное число витков пружины:

Для определения шага навивки, для начала определим гарантированный зазор между двумя витками, исключающий касание витков:

где – поправочный коэффициент, зависящий от индекса пружины: получаем ;

– максимальный диаметр проволоки: .

Определяем длину пружины в полностью сжатом состоянии:

Определяем длину пружины в свободном состоянии:

Определяем длину проволоки необходимую для изготовления пружины: