Расчетно-графическая работа по изгибу балки

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

ОБНИНСКИЙ ИНСТИТУТ АТОМНОЙ ЭНЕРГЕТИКИ

филиал федерального государственного автономного образовательного учреждения высшего профессионального образования

«Национальный исследовательский ядерный университет МИФИ»

(ИАТЭ НИЯУ МИФИ)

Отделение Ядерной физики и технологий

Выполнил:

студент гр. ЯЭТ-БXX __________________ Фамилия О.Ю.

Проверил:

к.т.н., доцент __________________ Росляков А.А.

г. Обнинск 20XX год

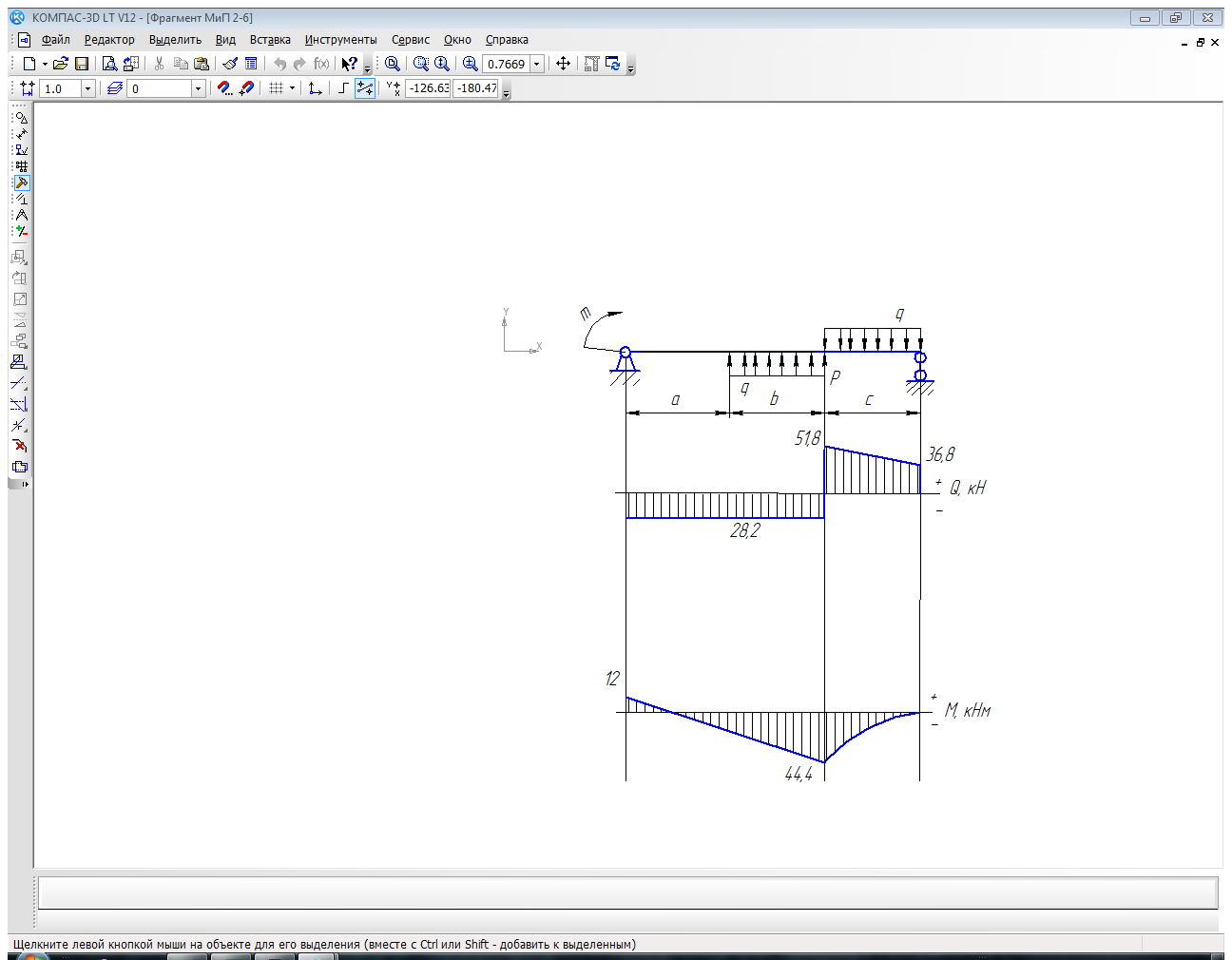
Вариант 6003

6)

0)

Вариант	0
Р, кН	12
т, кНм	10
q, кН/м	15

Вариант	0
а, м	1,2
b, м	1,0
с, м	1,5

Стандартный профиль

0)

3)

1. Построение эпюры поперечных сил Q и изгибающих моментов М

1. Нахождение реакций опор:

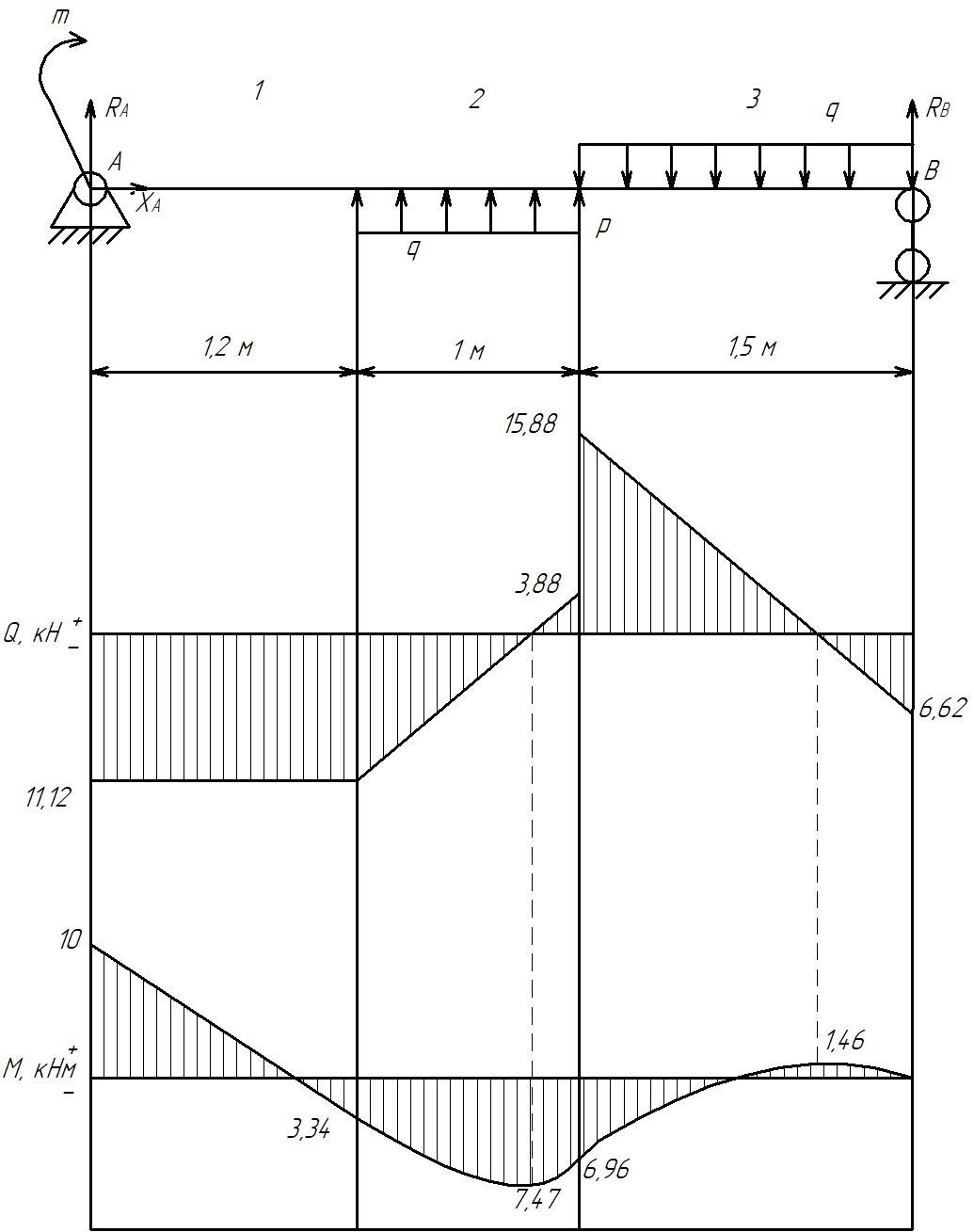
т. А: неподвижная шарнирная опора, следовательно, присутствует две реакции опоры: X_A и R_A, направленные горизонтально и вертикально соответственно.

т. В: подвижная шарнирная опора, следовательно, присутствует одна вертикальная реакция опоры R_B

Рассмотрим сумму моментов всех сил относительно т. А:

∑M_A = 0

-m + q*1*(1,2 + 1/2) - q*1.5*(2.2 + 1.5/2) + p*2.2+R_B*3.7 = 0

R_B = (m - q*1*(1,2 + 1/2) + q*1.5*(2.2 + 1.5/2)-p*2.2)/3,7

R_B = (10-15*1*(1,2 + 1/2) + 15*1.5*(2.2 + 1.5/2) - 12*2.2)/3,7

R_B = 6,61 (кН)

Рассмотрим сумму моментов всех сил относительно т. B:

∑M_B = 0

q*1.5*1.5/2 - q*1*(1.5 + 1/2) - p*1.5 -R_A*3.7 - m = 0

R_A = q*1.5*1.5/2 - q*1*(1.5 + 1/2) - p*1.5 - m

R_A = 15*1.5*1.5/2 - 15*1*(1.5 + 1/2) - 12*1.5 - 10

R_A = -11,12 (кН)

Для проверки вычислим сумму проекций всех сил на вертикальную ось.

∑F_y=0

R_A + q*1 + p - q*1.5 + R_B = 0

-11.12 + 15*1 + 12 - 15*1.5 + 6.61 = 0

-0.01 ≈ 0

2. Вычисление изгибающих моментов M:

Разделим балку на три участка. Начнем рассматривать балку слева направо.

1. Проведем сечение участка 1 и рассмотрим его левую часть:

M₁(z) = m + R_A*z 0 ≤ z < 1.2

M₁(0) = 10 - 11.12*0 = 10 (кНм)

M₁(1.2) =10 - 11.12*1.2 = -3,34 (кНм)

2. Проведем сечение участка 2 и рассмотрим его левую часть:

M₂(z) = m + R_A*z + q*(z-1.2)²/2 1.2 ≤ z < 2.2

M₂(1.2) = 10 – 11,12*1.2 + 15*(1.2-1.2)²/2 = -3,34 (кНм)

M₂(2,2) = 10 – 11,12*2,2 + 15*(2,2-1.2)²/2 = -6,96 (кНм)

3. Проведем сечение участка 3 и рассмотрим его левую часть:

M₃(z) = m + R_A*z + q*(z-1.2)²/2 – q*(z-2,2)²/2 – q*(z-2,2)²/2 + p*(z - 2.2) 2.2 ≤ z < 3.7

M₃(2.2) = 10 -11.12*2.2 + 15*(2.2-1.2)²/2 – 15*(2.2-2,2)²/2 - 15*(2.2-2,2)²/2 + 12*(2.2 - 2.2) =

= -6.96 (кНм)

M₃(3.7) = 10 -11.12*3.7 + 15*(3.7-1.2)²/2 – 15*(3.7-2,2)²/2 - 15*(3.7-2,2)²/2 + 12*(3.7 - 2.2) =

= 0 (кНм)

3. Вычисление поперечных сил Q:

Найдем поперечные силы, исходя их того факта, что они являются производными от изгибающих моментов, то есть Q = M’_z

1. Q₁ = M₁’_z = (m + R_A*z)’_z = R_A 0 ≤ z < 1.2

Q₁ = -11.12 (кН)

2. Q₂ = M₂’_z = (m + R_A*z + q*(z-1.2)²/2)’_z = R_A + q*(z-1.2) 1.2 ≤ z < 2.2

Q₂(1.2) = -11.12+15*(1.2-1.2) = -11.12 (кН)

Q₂(2.2) = -11.12+15*(2.2-1.2) = 3.88 (кН)

3. Q₃ = M₃’_z = (m + R_A*z + q*(z-1.2)²/2 – q*(z-2,2)²/2 – q*(z-2,2)²/2 + p*(z - 2.2))’_z = R_A +

+ q*(z-1.2) – q*(z-2.2) – q*(z-2.2) + p 2.2 ≤ z < 3.7

Q₃(2.2) = -11,12 + 15*(2.2-1.2) – 1.5*(2.2-2.2) – 15*(2.2-2.2) + 12 = 15.88 (кН)

Q₃(3.7) = -11,12 + 15*(3.7-1.2) – 1.5*(3.7-2.2) – 15*(3.7-2.2) + 12 = -6,62 (кН)

1.4 Найдем экстремумы изгибающих моментов:

Q₂ = 0 -11.12 + 15*(z-1.2) = 0

z = 11.12/15 + 1.2 = 1.94

M₂(1.94) = 10 - 11.12*1.94 + 15*(1.94-1.2)²/2 = -7.47 (кНм)

Q₃ = 0 -11.12 + 15*(z-1.2) – 15*(z-2.2) – 15*(z-2.2) + p = 0

z = 3.26

M₃(3.26) = 10 -11.12*3.26 + 15*(3.26-1.2)²/2 – 15*(3.26-2,2)²/2 –

• 15*(3.26-2,2)²/2 + 12*(3.26 - 2.2) = 1.46 (кНм)

1.5 С помощью полученных данных построим эпюру поперечных сил Q и изгибающих моментов М

2. Подбор по условию прочности размеров сечения из стандартного профиля (двутавра или швеллеров)

Найдем допускаемое напряжение:

[σ]= σ_t/n = 240/1.5 = (160 МПа)

Формула для проектировочного расчета:

W_x ≥ M_max/[σ] = 10*10³/160*10⁶ = 62.5 (см³)

Номер двутавра, момент сопротивления изгибу которого больше и наиболее ближе

к найденному, найдем по сортаменту прокатной стали. Выберем двутавр №14, имеющий

момент сопротивления изгибу 81,7 см³.

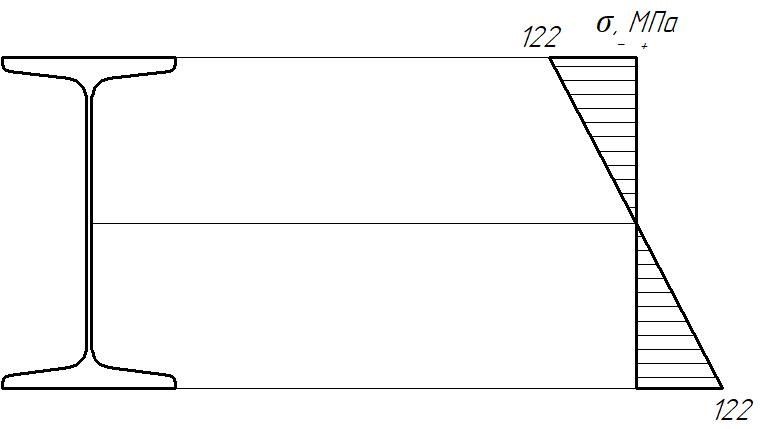
3. Построение эпюры для нормальных напряжений в опасном сечении балки с указанием максимальных напряжений.

Наибольшее нормальное напряжение в двутавре:

σ_max = M_max/W_x=10*10³/81.7*10^-6 = 122 (МПа)

4. Составление и решение дифференциального уравнения изогнутой оси балки, построение в масштабе графика изогнутой оси. Определение максимального прогиба балки.

Приближенное дифференциальное уравнения оси изогнутой оси балки:

E*J_x*y’’ = M(z)

Составим дифференциальные уравнения изогнутой оси балки для каждого участка:

E*J_x*y₁’’ = m + R_A*z 0 ≤ z < 1.2

E*J_x*y₂’’ = m + R_A*z + q*(z-1.2)²/2 1.2 ≤ z < 2.2

E*J_x*y₃’’ = m + R_A*z + q*(z-1.2)²/2 – q*(z-2,2)² + p*(z - 2.2) 2.2 ≤ z < 3.7

Проинтегрируем:

E*J_x*y₁’ = m*z + R_A*z²/2 + C₁ 0 ≤ z < 1.2

E*J_x*y₂’ = m*z + R_A*z²/2 + q*(z-1.2)³/6 + C₂ 1.2 ≤ z < 2.2

E*J_x*y₃’ = m*z + R_A*z²/2 + q*(z-1.2)³/6 – q*(z-2,2)³/3 + p*(z - 2.2)²/2 +C₃

2.2 ≤ z < 3.7

Граничные условия:

z = 1.2 y₁ = y₂

y₁’ = y₂’

z = 2.2 y₂ = y₃

y₂’ = y₃’

Из этого следует, что C₁ = C₂ = C₃ = C

Еще раз проинтегрируем:

E*J_x*y₁ = m*z²/2 + R_A*z³/6 + C*z + D₁ 0 ≤ z < 1.2

E*J_x*y₂ = m*z²/2 + R_A*z³/6 + q*(z-1.2)⁴/24 + C*z + D₂ 1.2 ≤ z < 2.2

E*J_x*y₃ = m*z²/2 + R_A*z³/6 + q*(z-1.2)⁴/24 – q*(z-2,2)⁴/12 + p*(z - 2.2)³/6 + C*z + D₃

2.2 ≤ z < 3.7

Граничные условия:

z = 1.2 y₁ = y₂

y₁’ = y₂’

z = 2.2 y₂ = y₃

y₂’ = y₃’

Из этого следует, что D₁ = D₂ = D₃ = D

Из условия для прогиба на левой опоре:

z = 0 y₁(0) = 0, следовательно D = 0

Из условия для прогиба на правой опоре:

z = 3.7 y₃(3.7) = 0, следовательно:

10*3.7²/2 -11.12*3.7³/6 + 15*(3.7-1.2)⁴/24 – 15*(3.7-2,2)⁴/12 + 12*(3.7 - 2.2)³/6+

+C*3.7+ 0 = 0

C = 0.16

Дифференциальные уравнения изогнутой оси балки:

y₁ = (5*z² -1.85*z³ + 0.16*z)/ E*J_x 0 ≤ z < 1.2

y₂ = (5*z² -1.85*z³ + 0.625*(z-1.2)⁴ + 0.16*z)/ E*J_x 1.2 ≤ z < 2.2

y₃ = (5*z² -1.85*z³ + 0.625*(z-1.2)⁴ – 1.25*(z-2,2)⁴ + 2*(z - 2.2)³ + 0.16*z)/E*J_x

2.2 ≤ z < 3.7

График изогнутой оси:

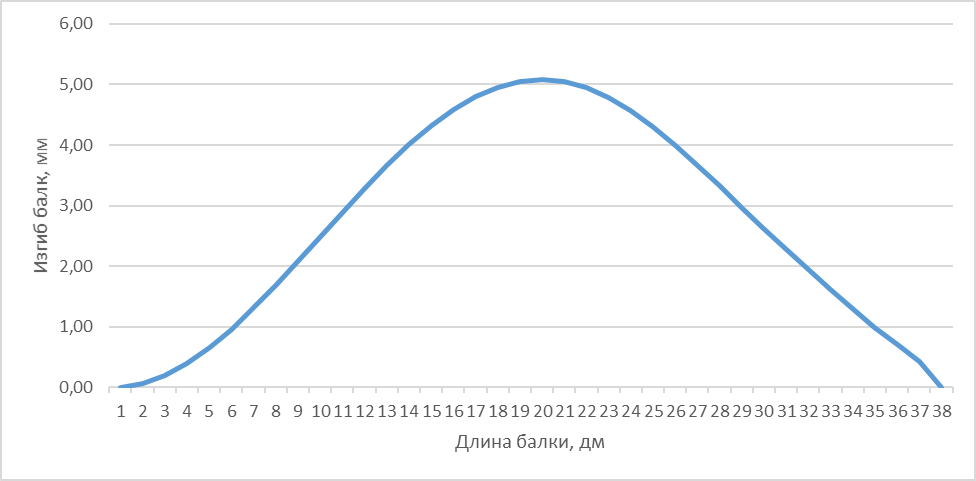
Определение максимального изгиба балки:

Из графика видно, что максимальный прогиб балки находится на 2 участке.

y₂’(z) = 0

10*z – 5.56*z² + 2.5*(z-1.2)³ + 0.16 = 0

z = 1.89 y_max = 5,08 (мм)

5. Определение с помощью интеграла Мора прогиба балки посередине между опорами

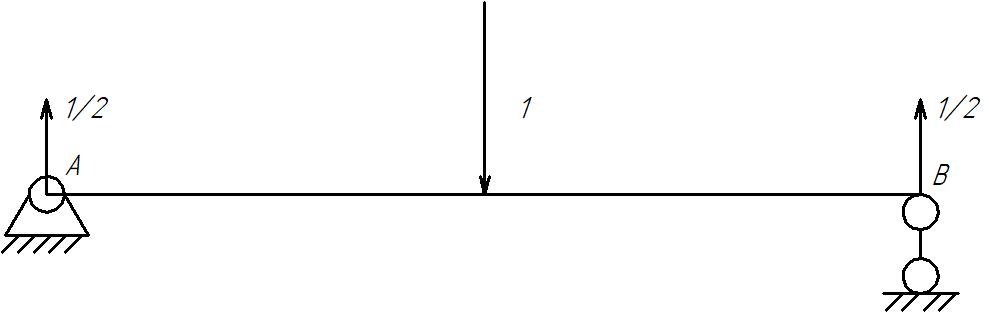
Для определения прогиба балки посередине между опорами приложим единичную силу в данной точке:

Интеграл Мора:

M₁ = 0.5*z 0 ≤ z < 1.85

M₂ = 0.5*(3.7-z) 1.85 ≤ z < 3.7

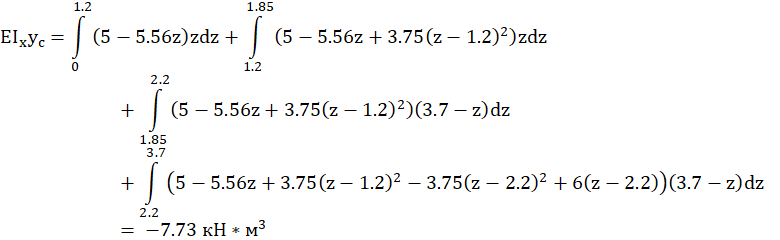
Прогиб балки посередине между опорами составил:

Y_c = 7.73/E*J_x = 5,07 (мм)

6. Проверить выполнение условия жесткости, приняв допускаемый прогиб:

,

где l – длина пролета балки.

Определяем допускаемый прогиб:

[f]=3700/500=7,4 (мм)

y_max < [f] следовательно, условие жесткости выполняется.