МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ федеральное государственное АВТОНОМНОЕ образовательное учреждение ВЫСШЕГО образования «Национальный исследовательский ядерный университет «МИФИ»

Обнинский институт атомной энергетики – филиал федерального государственного автономного образовательного учреждения высшего образования «Национальный исследовательский ядерный университет «МИФИ» (ИАТЭ НИЯУ МИФИ)

Отделение Ядерной физики и технологий Лабораторная работа №1

Теплоотдача вертикального цилиндра при естественной конвекции

Выполнил: студент гр. МН-БXX		Фамилия И.О.
Проверил: д.т.н. профессор (О)ЯФиТ		Чусов И.А.

Обнинск, 20XX г

1. Цель работы

Изучение естественной конвекции вдоль вертикального цилиндра и составление функциональной зависимости между числами Нуссельта, Прандтля и Грасгофа.

2. Теоретические основы

Одним из способов переноса тепла является конвекция, когда частицы среды (газ, жидкость) меняют свое положение в пространстве и, таким образом, переносят тепло. Этот процесс в значительной мере определяется скоростью перемещения частиц среды и всегда сопровождается теплопроводностью, т.е. он происходит не только под действием градиента температуры, но и совместно с движущейся средой.

Область, в которой жидкость замедляется под действием сил вязкости, называется гидродинамическим пограничным слоем. За пределами пограничного слоя градиент скорости настолько мал, что касательными напряжениями можно пренебречь. Область вблизи стенки, где происходит основная часть изменения температуры, называется тепловым (температурным) пограничным слоем.

Если движение текучей среды возникает под действием неоднородного поля массовых сил (градиент плотности, сила тяжести, центробежные силы), то такой процесс называют свободной или естественной конвекцией.

Интенсивность теплообмена определяется разностью температур тела и окружающего теплоносителя, физическими свойствами теплоносителя и геометрическими факторами.

Количество переданного тепла определяется по закону Ньютона-Рихмана:

,

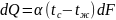где t_c – средняя температура поверхности тела, ºС

t_ж – температура теплоносителя вдали от поверхности, ºС

F – поверхность теплообмена, м²

Коэффициент пропорциональности α [Вт/м²К] называется коэффициентом теплоотдачи (теплообмена). Численно он равен количеству тепла, передаваемому через 1 м² поверхности за единицу времени при разности температур поверхности и жидкости 1 К. Физический смысл понятия коэффициент теплообмена можно установить из рассмотрения условий на границе тела, охлаждаемого жидкостью. Температура охлаждающей поверхности жидкости изменяется в основном в тепловом пограничном слое толщиной δ, где процесс переноса тепла в значительной степени определяется теплопроводностью. Поэтому коэффициент теплообмена можно трактовать как средний по поверхности безразмерный градиент температуры на границе тела с потоком жидкости. В общем случае коэффициент теплоотдачи является функцией формы и размеров тела, режима движения, скорости и температуры жидкости физических параметров жидкости и других величин.

Для полного описания процессов конвективного теплообмена необходимо задать систему дифференциальных уравнений, выражающих законы сохранения массы, импульса, энергии, и условия однозначности, включающие в себя начальные (задание температуры в начальный момент времени), граничные (скорости, температуры в начальный момент времени), граничные (скорости, температуры на границах и т.д.), геометрические (форма и размеры тела), физические (свойства среды). Исходные уравнения и их решение можно представить в виде зависимостей между безразмерными комплексами – критериями. В условиях свободной конвекции достаточно рассмотреть следующие три безразмерных критерия:

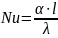– число Нуссельта;

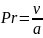– число Прандтля;

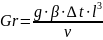– число Грасгофа,

где 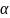– коэффициент теплоотдачи, 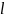- определяющий размер, λ - коэффициент теплопроводности жидкости, υ – коэффициент кинематической вязкости, а – коэффициент температурапроводности, g - ускорение свободного падения, β коэффициент термического расширения.

Число Нуссельта характеризует теплообмен на границе стенка-жидкость и показывает меру отношения, определяющего (характерного) размера к толщине пограничного слоя.

Число Прандтля является физическим параметром среды и характеризует отношение между полями скоростей и температур.

Число Грасгофа характеризует подъёмную силу, возникшую в жидкости вследствие разности плотностей.

На основе многочисленных экспериментальных данных было установлено, что число Нуссельта можно связать с числами Грасгофа и Прандтля соотношением:

Nu = c∙(Gr∙Pr)ⁿ,

где c и n определяются экспериментально.