4. Расчет валов привода

4.1 Проектный расчет всех валов привода

Расчет диаметров шеек валов под зубчатое колесо производим по формуле:

= ; (4.1)

где Т – момент на валу, Н ⋅ м; [τ] – допускаемые напряжения кручения, МПа

Диаметр остальных шеек валов принимаем по конструктивным соображениям ориентируясь на рассчитанный диаметр шейки вала под зубчатое колесо.

Производим расчет быстроходного вала редуктора:

= = 32,2 мм.

Принимаем диаметр = 35 мм, диаметр под подшипник = 30 мм, диаметр выходного конца вала = 25 мм.

Производим расчет промежуточного вала редуктора:

= = 49,53 мм.

Принимаем диаметр = 50 мм, диаметр под подшипник = 45 мм, диаметр выходного конца вала = 40 мм.

Производим расчет тихоходного вала редуктора:

= = 70,98 мм.

Принимаем диаметр = 70 мм, диаметр под подшипник = 65 мм, диаметр выходного конца вала = 60 мм.

Производим расчет приводного вала редуктора:

= = 70,27 мм.

Принимаем диаметр = 70 мм, диаметр под подшипник = 65 мм, диаметр выходного конца вала = 60 мм.

4.2 Проверочный расчет тихоходного вала редуктора на усталостную выносливость

Исходные данные:

В качестве примера рассчитаем промежуточный вал двуступенчатого редуктора в составе привода цепного конвейера, устанавливаем, что вращающий момент, действующий на промежуточный вал редуктора, Т = 316,03 Н·м, а частота вращения вала n = 86,01 мин^‒1. На валу III установлены косозубое цилиндрическое колесо, подшипники и шестерня. Из предыдущих расчетов делительный диаметр колеса d₂ = 200 мм, ширина колеса b_w = 39 мм, делительный диаметр шестерни d₁ = 83,67 мм, ширина колеса b_w = 60 мм. В качестве материала вала выбираем сталь 40Х, улучшенную, = 850 Мпа, = 550 Мпа.

Определяем средний диаметр редукторного тихоходного вала при [τ] =14 МПа по формуле:

= = 49,53 мм.

Определяем нагрузки, действующие на вал. Составляющие нормальной силы в зацеплении зубчатых колес получаем по результатам расчета тихоходной и быстроходной цилиндрической передачи: окружная сила = 2194,19 H, радиальная сила = 807,8 H, осевая сила = 333,8 H, окружная сила = 7554,2 H, радиальная сила = 2777,07 H, осевая сила = 1072,43 H.

Осевая сила создает изгибающий момент

= ⋅ ; (4.2)

= 333,8 ⋅ = 33,38 ⋅ H ⋅ мм;

= 1072,43 ⋅ = 44,865 ⋅ H ⋅ мм.

В рассматриваемом случае выбираем подшипники роликовый конический однорядный средней серии 7309 с углом α = 11°. Их размеры: внутренний диаметр d_п = 45 мм, наружный диаметр D_п = 100 мм, ширина b_п = 25 мм.

Определяем диаметры поверхностей ступеней вала:

= 50 мм, = 50 мм, = 45 мм, = 50 мм, = 55 мм, = 50 мм, = 45 мм, = 48 мм.

Определяем длины участков вала:

= 39 + 10 = 49 мм, = 60 + 10 = 70 мм, = 25 мм, = 20 мм, = 10 мм, = 65 мм, = 25 мм, = 20 мм.

Определение точки приложения реакций подшипников:

a = ; (4.4)

a = = 21 мм.

Определяем реакции в опорах из условий равновесия (сумма моментов сил равна нулю относительно одной и второй опор).

Находим реакции опор в горизонтальной плоскости (см. рис. 2, б).

В горизонтальной плоскости сумма моментов относительно точки А равна нулю:

 0: − ⋅ + ⋅ ( + + ) − ⋅ ( + ) = 0. (4.5)

= ; (4.6)

= = 6041,47 H.

В горизонтальной плоскости сумма моментов относительно точки В равна нулю:

 0: − ⋅ ( + + ) + ⋅ + ⋅ ( + ) = 0. (4.7)

= ; (4.8)

= = 3706,92 H.

В качестве проверки записываем уравнение равенства нулю суммы всех сил на ось OY в горизонтальной плоскости:

 0: + − − = 0. (4.9)

 0: 3706,92 + 6041,47 − 2194,19 – 7554,2 = 0.

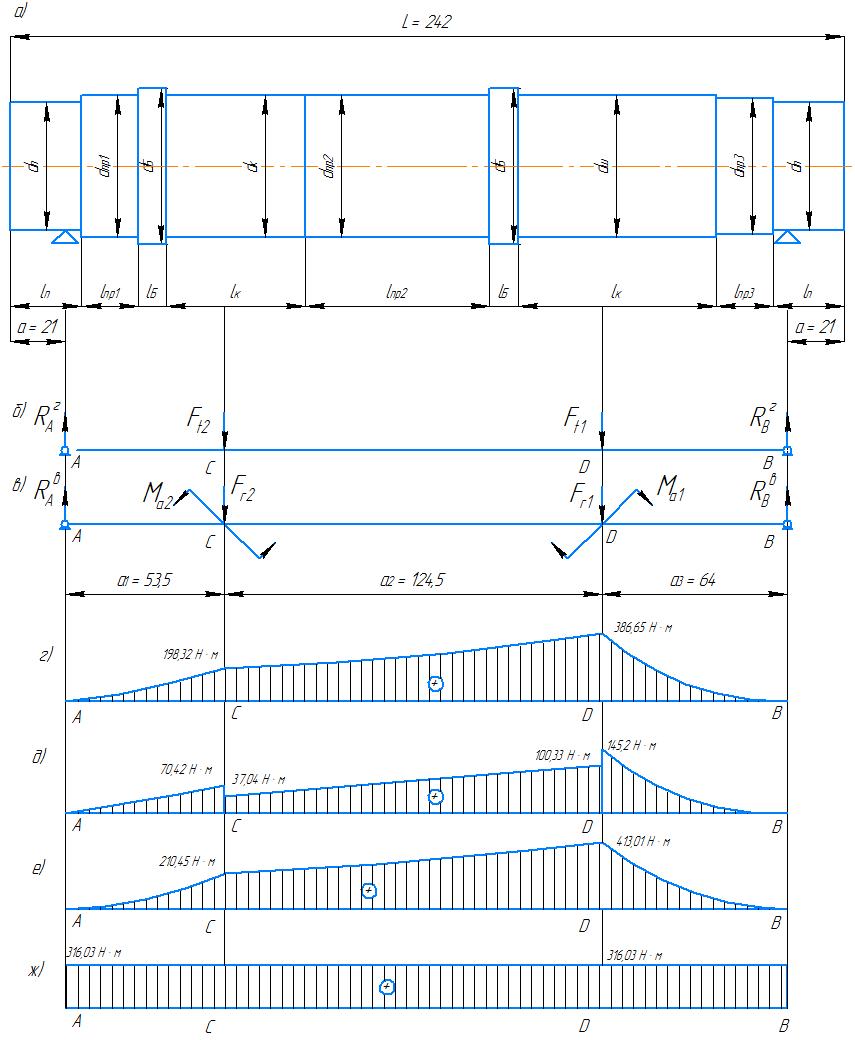
Рисунок 2 – Расчетные схемы и эпюры моментов для тихоходного вала редуктора

Проектирование вала: а ‒ эскиз вала; б ‒ расчетная схема в горизонтальной плоскости; в ‒ расчетная схема в вертикальной плоскости; г ‒ эпюра изгибающих моментов в горизонтальной плоскости; д ‒ эпюра изгибающих моментов в вертикальной плоскости; е ‒ эпюра суммарных изгибающих моментов; ж ‒ эпюра вращающих моментов.

Находим реакции опор в вертикальной плоскости (см. рис. 2, в).

В вертикальной плоскости сумма моментов относительно точки А равна нулю:

 0: − ⋅ + ⋅ ( + + ) − + − ⋅ ( + ) = 0. (4.10)

= ; (4.11)

= = 2268,68 H.

Момент M_a подставляем в ньютон-миллиметрах (умножаем на 10³), а длины участков ‒ в миллиметрах, чтобы снизить погрешность вычислений.

В вертикальной плоскости сумма моментов относительно точки В равна нулю:

 0: − ⋅ ( + + ) + ⋅ + ⋅ ( + ) − + = 0. (4.12)

= ; (4.13)

= = 1316,19 H.

В качестве проверки записываем уравнение равенства нулю суммы всех сил на ось OY в вертикальной плоскости:

 0: + − − = 0. (4.14)

 0: 1316,19 + 2268,68 – 2777,07 – 807,8 = 0.

Находим модули суммарных радиальных реакций опор:

= ; (4.15)

= = 3933,65 H;

= ; (4.16)

= = 6453,39 H.

Строим эпюры изгибающих и крутящих моментов (рис. 2, г‒ж) по узловым точкам.

Эпюру изгибающих моментов в горизонтальной плоскости (расчетная схема на рис. 2, б) строим следующим образом. Положительные значения откладываем на сжатых волокнах. В крайних точках вала А и D изгибающий момент равен нулю. Если расчет вести от опоры А (слева направо), то момент в точке С будет возникать от действия реакции . Его модуль

= ⋅ ; (4.17)

= 3706,92 ⋅ 53,5 ⋅ = 198,32 H.

Эпюру изгибающих моментов в горизонтальной плоскости (расчетная схема на рис. 2, б) строим следующим образом. Положительные значения откладываем на сжатых волокнах. В крайних точках вала B и C изгибающий момент равен нулю. Если расчет вести от опоры B (слева направо), то момент в точке D будет возникать от действия реакции . Его модуль

= ; (4.18)

= 6041,47 ⋅ 64 ⋅ = 386,65 H.

Соединив четыре узловые точки отрезками, получим эпюру изгибающих моментов, действующих на вал в горизонтальной плоскости (см. рис. 2, г).

При построении эпюры изгибающих моментов в вертикальной плоскости (расчетная схема на рис. 2, в) нужно учесть, что выходной конец вала не нагружен, поэтому расчет ведем от опоры А (слева направо) и от опоры В (справа налево), определяя момент в точке С:

= ⋅ ; (4.19)

= 1316,19 ⋅ 53,5 ⋅ = 70,42 H;

= ⋅ − + ; (4.20)

= 2268,68 ⋅ (64 + 124,5) ⋅ − 2777,07 ⋅ 124,5 ⋅ − 44,865 = 37,04 H.

Строим эпюру изгибающих моментов в вертикальной плоскости аналогичным образом (см. рис. 2, д) по узловым точкам.

Несовпадение значений моментов в точке С при расчете от опоры А и от опоры В не случайно. В качестве проверки определяем разницу этих значений: 70,42 ‒ 37,04 = 33,38 H ⋅ м, что соответствует моменту M_a2, рассчитанному по формуле с учетом единиц измерения и погрешности вычислений.

При построении эпюры изгибающих моментов в вертикальной плоскости (расчетная схема на рис. 2, в) нужно учесть, что выходной конец вала не нагружен, поэтому расчет ведем от опоры В (справа налево) и от опоры А (слева направо), определяя момент в точке D:

= ⋅ ; (4.21)

= 2268,68 ⋅ 64 ⋅ = 145,2 H;

= ⋅ − − ; (4.22)

= 1316,19 ⋅ (53,5 + 124,5) ⋅ − 807,8 ⋅ 124,5 ⋅ − 33,38 = 100,33 H.

Строим эпюру изгибающих моментов в вертикальной плоскости аналогичным образом (см. рис. 2, д) по узловым точкам.

Несовпадение значений моментов в точке D при расчете от опоры А и от опоры В не случайно. В качестве проверки определяем разницу этих значений: 145,2 ‒ 100,33 = 44,865 H ⋅ м, что соответствует моменту M_a1, рассчитанному по формуле с учетом единиц измерения и погрешности вычислений.

Строим суммарную эпюру изгибающих моментов (см. рис. 2, е). Момент снова определяем в каждой из четырех точек как геометрическую сумму моментов в этих точках в горизонтальной и вертикальной плоскостях:

= ; (4.23)

= = 0 H ⋅ м;

= ; (4.24)

= = 210,45 H ⋅ м;

= ; (4.25)

= = 413,01 H ⋅ м;

= ; (4.26)

= = 0 H ⋅ м.

Определяем опасное сечение (опасные сечения).

Таким образом, в опасном сечении изгибающий момент = 413,01 H ⋅ м, вращающий момент T = 316,03 H ⋅ м.

Определяем напряжения изгиба и кручения.

Напряжения изгиба

= ; (4.27)

= = 45,32 МПа.

Напряжения кручения

= ; (4.28)

= = 17,34 МПа.

Определяем пределы выносливости, прочности и составляющие действующих напряжений.

Пределы выносливости по напряжениям изгиба σ_‒1, кручения τ_‒1 и предел прочности по напряжениям кручения τ_B определяем по следующим зависимостям:

σ_‒1 = 0,4 ⋅ ; (4.29)

σ_‒1 = 0,4 ⋅ 850 = 340 Мпа;

τ_‒1 = 0,2 ⋅ ; (4.30)

τ_‒1 = 0,2 ⋅ 850 = 170 Мпа;

τ_B = 0,6 ⋅ ; (4.31)

τ_B = 0,6 ⋅ 850 = 510 Мпа.

Амплитудные и средние составляющие действующих напряжений

= 0; = = 45,32 МПа;

= = 0,5 ⋅ = 0,5 ⋅ 17,34 = 8,67 МПа.

Находим коэффициенты, входящие в формулы для определения запасов сопротивления усталости.

Коэффициент (показатель степени) в формуле для расчета масштабного фактора при изгибе

= 0,19 – 1,25 ⋅ ⋅ ; (4.32)

= 0,19 – 1,25 ⋅ ⋅ 850 = 0,083.

При кручении

= 1,5 ⋅ ; (4.33)

= 1,5 ⋅ 0,083 = 0,1245.

Масштабный фактор при изгибе

= 0,5 ⋅ ; (4.34)

= 0,5 ⋅ = 0,871.

Масштабный фактор при кручении

= 0,5 ⋅ ; (4.35)

= 0,5 ⋅ = 0,82.

Устанавливаем шероховатость поверхности вала R_z = 3,2 мкм, кроме поверхностей под колесо, подшипники, где R_z = 1,6 мкм. Коэффициент, учитывающий качество (шероховатость) поверхности по изгибу,

= 1 – 0,22 ⋅ ⋅ ; (4.36)

= 1 – 0,22 ⋅ ⋅ = 0,971.

Коэффициент, учитывающий качество (шероховатость) поверхности по кручению,

= 0,575 ⋅ + 0,425; (4.37)

= 0,575 ⋅ 0,971 + 0,425 = 0,983.

Определяем эффективные коэффициенты концентрации напряжений по изгибу K_σ и кручению K_τ. Они зависят от вида концентраторов напряжений в опасном сечении. Возможны несколько вариантов.

Случай 1. Если исследуется сечение вала, где с натягом установлена какая-нибудь деталь (зубчатое колесо, шкив, полумуфта и др.), то определяется отношение

= ⋅ ⋅ ; (4.38)

где K₁ ‒ коэффициент, K₁  0,38  1,48 ⋅ lgd , если d < 150 мм, K₁ = 3,6 при d ≥ 150 мм; K₂ ‒ коэффициент, K₂  0,305 + 0,0014  ; K₃ ‒ коэффициент, K₃  0,65  0,014 ⋅ p , если p ≤ 25 МПа, K3 = 1 при p > 25 МПа.

Давление p должно определяться исходя из прочности прессового соединения. Предварительно можно считать, что p > 25 МПа, если передаваемый момент T ≥ 900 H ⋅ м.

K₁  0,38  1,48 ⋅ lgd ; (4.39)

K₁  0,38  1,48 ⋅ lg49,53 = 2,88;

K₂  0,305 + 0,0014  ; (4.40)

K₂  0,305 + 0,0014  850 = 1,495;

K₃  1;

= 2,88 ⋅ 1,495 ⋅ 1 = 4,3.

При изгибе отношение

= 0,6 ⋅ ; (4.41)

= 0,6 ⋅ 4,3 = 2,58.

Случай 2. Если исследуется сечение вала, где имеется ступенчатый галтельный переход, то эффективные коэффициенты концентрации напряжений по изгибу K_σ и кручению K_τ определяются:

t = 0,5 ⋅ ( ); (4.42)

t = 0,5 ⋅ (48 ) = 1,5 мм.

Принимаем нестандартное значение r = 0,5 мм. Отношения:

= = 3;

= = 0,01.

Тогда принимаем = 2,1, = 1,65 и отношение:

= = 2,41;

= = 2,01.

Случай 3. Если исследуется сечение вала, где имеется шпоночный паз, то коэффициенты K_σ и K_τ определяются = 1,7 , = 2,05.

Если поверхностное упрочнение азотирование (как в рассматриваемом случае), K_V = 3,0.

Определяем коэффициенты концентрации напряжений в опасном сечении при изгибе и кручении соответственно:

= ; (4.43)

= = 1,44;

= ; (4.44)

= = 0,865.

Коэффициенты, корректирующие влияние постоянной составляющей цикла напряжений на сопротивление усталости по изгибу и кручению,

= 0,02 + 2 ⋅ ⋅ ; (4.45)

= 0,02 + 2 ⋅ ⋅ 850 = 0,19;

= 0,5 ⋅ ; (4.46)

= 0,5 ⋅ 0,19 = 0,095.

Определяем запасы сопротивления усталости.

Запас сопротивления усталости при изгибе

= ; (4.47)

= = 5,2.

Запас сопротивления усталости при кручении

= ; (4.48)

= = 20,42.

Общий запас сопротивления усталости

= = 1,5; (4.49)

= = 5,04 = 1,5.

где [s] ‒ минимальный допускаемый запас сопротивления усталости.

Усталостная прочность вала обеспечена.