2.4 Проверочный расчет тихоходной передачи

Выполняем проверочный расчет передачи по контактным напряжениям. Условие прочности записываем следующим образом:

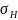= 1,18 ⋅ 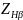⋅ 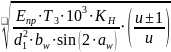; (2.35)

где T₃ ‒ момент на шестерне, H·м; Z_Hβ ‒ коэффициент повышения прочности прямозубых передач по контактным напряжениям; E_пр ‒ модуль упругости, E_пр = 2 · E₁ · E₂/(E₁ + E₂), для стальных зубчатых колес E_пр  2,1  10⁵ МПа; K_H ‒ коэффициент расчетной нагрузки.

Рассчитываем коэффициенты перекрытия. Для нефланкированных передач без смещения коэффициент торцового перекрытия

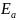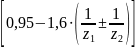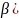= ⋅ (1 + cos( ) ⋅ cos(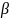 ); (2.36)

= ⋅ (1 + cos(14,53)) ⋅ cos(14,53) = 1,7.

Коэффициент Z_Hβ определяем по формуле:

Z_Hβ = 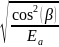; (2.37)

Z_Hβ = 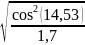= 0,742.

Коэффициент расчетной нагрузки:

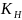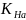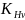= ⋅ ⋅ ; (2.38)

где K_Hα ‒ коэффициент распределения нагрузки между зубьями; K_Hβ ‒ коэффициент концентрации нагрузки. Определен ранее по графикам, а как K_Hβ = 1,45; K_H ‒ коэффициент динамической нагрузки.

Коэффициент распределения нагрузки между зубьями находим по формуле:

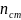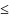
= 1 + C ⋅ ( – 5) 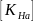; (2.39)

где С – коэффициент твердости и типа зубьев. С = 0,06 – для прямозубых передач, С = 0,15 ‒ для косозубых передач при твердости зубьев колеса и шестерни более 350 HB, С = 0,25 ‒ если твердость зубьев колеса меньше либо равна 350 HB; nст ‒ степень точности изготовления колес, nст = 5…9; [K_Hα] ‒ допускаемое значение коэффициента K_Hα. [K_Hα] = 1,25 ‒ для прямозубых передач, [K_Hα] = 1,6 ‒ для косозубых.

В рассматриваемом примере

= 1 + 0,15 ⋅ (7– 5) = 1,3 1,6.

Для определения коэффициента динамической нагрузки K_Hυ необходимо знать окружную скорость υ.

v₁ = 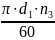; (2.40)

v₁ = 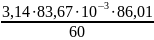= 0,376 м/с.

Коэффициент K_Hυ можно найти по табл. В.1. Если окружная скорость υ ≤ 1 м/c, данный коэффициент принимаем KHυ = 1,0.

= 1,3 ⋅ 1 ⋅ 1,04 = 1,352;

Таким образом

= 1,18 ⋅ 0,742 ⋅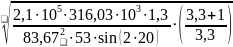 = 601,12 МПа;

< [ ] = 609,5 МПа.

Контактная прочность передачи обеспечена. Перегрузка составляет:

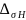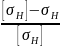= ⋅ 100%; (2.41)

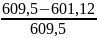= ⋅ 100% = 1,13 %.

Выполняем проверочный расчет прочности передачи по напряжениям изгиба:

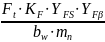
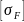= ; (2.42)

где F_t ‒ окружная сила, H; K_F ‒ коэффициент расчетной нагрузки по напряжениям изгиба; Y_FS ‒ коэффициент формы зуба; Y_Fβ ‒ коэффициент повышения прочности косозубых передач по напряжениям изгиба.

Определяем силы, действующие в зацеплении. Значение окружной силы необходимо для расчета прочности на изгиб, другие составляющие – для дальнейшего расчета вала и подбора подшипников.

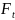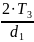= ; (2.43)

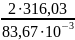= = 7554,2 H;

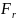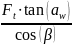= ; (2.44)

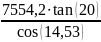= = 2840,35 H;

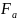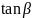= ⋅ ; (2.45)

= 7554,2 ⋅ 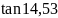= 1957,87 H.

Коэффициент формы зуба YFS выбираем по графику (рис. 2.6) при коэффициентах смещения x1 = x2 = 0 в зависимости от эквивалентного числа зубьев zv шестерни и колеса.

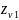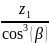= ; (2.46)

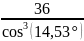= = 39,68.

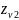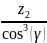= ; (2.47)

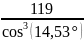= = 131,19.

При нулевом суммарном смещении для шестерни Y_FS1 = 3,78, для колеса Y_FS2 = 3,75. Для шестерни и для колеса находим отношение :

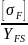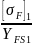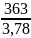= = 96,03;

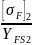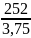= = 67,2.

Дальнейший расчет ведем по колесу, т. к. данное соотношение меньше. То есть принимаем [ ] = [ ]₂ = 252 МПа, Y_FS = Y_FS2 = 3,75.

Коэффициент Y_Fβ должен быть ≥ 0,7. Принимаем Y_Fβ = 0,7.

Коэффициент расчетной нагрузки K_F по напряжениям изгиба определяем аналогично коэффициенту K_H:

K_F  K_Fα ⋅ K_Fβ ⋅ K_Fυ; (2.48)

где K_Fα ‒ коэффициент распределения нагрузки между зубьями; K_Fβ ‒ коэффициент концентрации нагрузки; K_Fυ ‒ коэффициент динамической нагрузки.

При расчете на прочность по напряжениям изгиба принимаем K_Fα = K_Hα. Ранее определено K_Hα = 1,5. Значит, K_Fα = 1,5.

Коэффициент концентрации нагрузки K_Fβ выбираем по графикам в зависимости от твердости шестерни и колеса, вида расположения колес в редукторе и значения ψ_bd. Из графиков видно, что при ψ_bd = 0,75 K_Fβ = 1,04.

В рассматриваемом случае, т. к. окружная скорость υ ≤ 1 м/c, данный коэффициент можно принимать K_Fυ = 1,0.

Таким образом, коэффициент расчетной нагрузки по напряжениям изгиба KF определяем по формуле:

K_F  1,3 ⋅ 1,04 ⋅ 1 = 1,352.

Тогда по формуле:

= = 224,82 МПа [ ] = 252 МПа.

Перегрузка составляет:

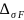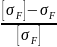= ⋅ 100%; (2.49)

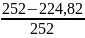= ⋅ 100% = 10,78 %.

Условие изгибной прочности выполняется.