4.3 Проверочный расчет тихоходного вала редуктора на статическую перегрузку и жесткость

При статических перегрузках напряжения, рассчитанные по формулам, удваиваются:

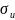= 29,83 ⋅ 2 = 59,66 Мпа; = 18,95 ⋅ 2 = 37,9 МПа.

Допускаемые значения напряжений принимаем

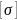= 0,8 ⋅

= 0,8 ⋅ 550 = 440 МПа

где σ_Т ‒ предел текучести материала вала. Для улучшенной стали 40Х σ_Т = 550 МПа.

Проверяем условие статической прочности при перегрузках, вычисляя эквивалентные напряжения:

=

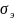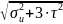
= = 88,7 МПа = 440 МПа

Условие статической прочности выполняется.

Проверяем жесткость вала. Опасным является прогиб вала под колесом. Момент инерции:

=

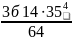= = 7,36 ⋅ мм⁴

Прогиб в горизонтальной плоскости от силы :

=

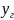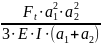
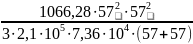= = 2,12 ⋅ мм.

Прогиб в вертикальной плоскости от силы F_r:

=

= = 0,775 ⋅ мм.

Прогиб в вертикальной плоскости от силы F_r:

=

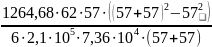= = 4,12 ⋅ мм.

Формулы для определения прогибов для различных сечений и способов нагружения вала.

Момент M_a прогиб в сечении под колесом не создает.

Суммарный максимально возможный прогиб

= +

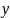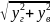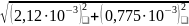= + 4,12 ⋅ = 6,377 мм.

Допускаемый прогиб можно ориентировочно определить по формуле:

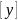= 0,01 ⋅ m

= 0,01 ⋅ 2,75 = 0,0275 мм.

Так как y = 0,006377 мм ≤ [y] = 0,0275 мм, жесткость вала обеспечена.

5. Подбор подшипников для валов привода

5.1 Предварительный выбор подшипников качения для всех валов привода и его обоснование

По диаметрам шеек валов под подшипники валов производим подбор подшипников, для установки валов в корпус редуктора. Так как во всех передачах в редукторе в зацеплении возникает осевая нагрузка, то для валов редуктора принимаем по ГОСТ 831-75 шариковые радиально-упорные однорядные подшипники.

Для входного вала принимаем подшипники 36302 со следующими основными размерами и характеристиками:

d = 15 мм – номинальный диаметр отверстия внутреннего кольца;

D = 42 мм – номинальный диаметр наружной цилиндрической поверхности наружного кольца;

B = 13 мм – номинальная ширина подшипника;

C = 13,6 кН – динамическая грузоподъемность;

C₀ = 6,8 кН – статическая грузоподъемность;

Для выходного вала принимаем подшипники 36306 со следующими основными размерами и характеристиками:

d = 30 мм – номинальный диаметр отверстия внутреннего кольца;

D = 72 мм – номинальный диаметр наружной цилиндрической поверхности наружного кольца;

B = 19 мм – номинальная ширина подшипника;

C = 26,9 кН – динамическая грузоподъемность;

C₀ = 20,4 кН – статическая грузоподъемность;

Для приводного вала принимаем подшипники 36309 со следующими основными размерами и характеристиками:

d = 45 мм – номинальный диаметр отверстия внутреннего кольца;

D = 100 мм – номинальный диаметр наружной цилиндрической поверхности наружного кольца;

B = 25 мм – номинальная ширина подшипника;

C = 50,5 кН – динамическая грузоподъемность;

C₀ = 41 кН – статическая грузоподъемность;

5.2 Проверочный расчет подшипников тихоходного вала на динамическую и статическую грузоподъёмность

В примере расчета тихоходного вала редуктора были подобраны подшипники радиально-упорные шариковые 36306 с углом α = 12°. Внутренний диаметр d_п = 30 мм, наружный диаметр D_п = 72 мм, ширина b_п = 19 мм. Необходимо обосновать выбор подшипников и проверить на статическую и динамическую грузоподъемность. Нагрузка с умеренными толчками, температура подшипника не превышает 100 °С.

Из примера расчета привода частота вращения тихоходного вала редуктора (вала III) n = 365 мин^‒1.

Из примера расчета тихоходной передачи редуктора ресурс привода t_Σ = 20400 ч. Режим нагружения средний равновероятный (режим II), допускается трехкратная перегрузка. Осевая сила, действующая в зубчатом зацеплении, определена по формуле: F_a = 615,33 Н. Из примера расчета вала суммарные радиальные реакции опор R_A = 1413,48 H, R_B = 1455,88 H.

Для выбранного подшипника 36309 уточняем по справочным данным паспортные (базовые) значения динамической грузоподъемности С = 26,9 кН, статической грузоподъемности С₀ = 20,4 кН.

Отношение осевой силы к базовой статической грузоподъемности:

= = 0,03

Интерполируя данные, находим

e = 0,34 − 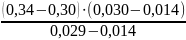= 0,297

Осевые составляющие реакций от радиальных нагрузок

= e ⋅

= 0,297 ⋅ 1413,48 = 419,8 H

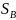= e ⋅

= 0,297 ⋅ 1455,88 = 432,4 H

Из условия равновесия сил, действующих вдоль оси вала

= − −

= +

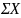= 615,33 + 432,4 = 1047,73 H

– условие выполняется

= −

= 1047,73 – 615,33 = 432,4 H

– условие выполняется

Так как задан режим работы II, принимаем K_E = 0,63.

Определяем средние величины реакций опор:

= ⋅

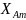= 0,63 ⋅ 1047,73 = 660,07 H

= ⋅

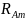= 0,63 ⋅ 1413,48 = 890,5 H

= ⋅

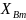= 0,63 ⋅ 432,4 = 272,4 H

= ⋅

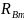= 0,63 ⋅ 1455,88 = 917,2 H

Уточняем соотношение для левого подшипника, где действует осевая реакция (и как более нагруженного), по формуле

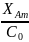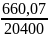= = 0,032 e = 0,032

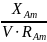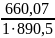= = 0,74 e = 0,74 > e = 0,34

Определяем коэффициент вращения колец V. Принимаем V = 1.

Уточняем соотношение для правого подшипника, где действует осевая реакция (и как более нагруженного), по формуле

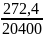= = 0,013 e = 0,032

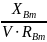= = 0,297 e = 0,297 e = 0,34

Определяем эквивалентную динамическую нагрузку, действующую на левый, более нагруженный подшипник:

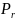= ( X ⋅ V ⋅ + Y ⋅ ) ⋅ ⋅

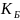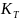
Имеем e = 0,74. При этом e = 0,74 > e = 0,34. Соответственно, X = 0,45, Y = 1,62.

Если рассматриваем радиальные шариковые подшипники, установленные на валу, где не действуют осевые силы (F_a = 0), или отношение F_a/C₀ меньше имеющегося (< 0,34), то X = 1, Y = 0.

Коэффициент безопасности принимаем K_Б = 1 ‒ при спокойной нагрузке. Температурный коэффициент принимаем K_Т = 1, если температура подшипника в процессе работы не превышает 100 °С.

= (0,45 ⋅ 1 ⋅ 890,5 + 1,62 ⋅ 660,07) ⋅ 1 ⋅ 1 = 1470,03 H

Определяем эквивалентную динамическую нагрузку, действующую на правый подшипник:

= ( X ⋅ V ⋅ + Y ⋅ ) ⋅ ⋅

= (1 ⋅ 1 ⋅ 917,2 + 0 ⋅ 272,4) ⋅ 1 ⋅ 1 = 917,2 H

Ресурс подшипника (в миллионах оборотов)

L =

L = = 446,76 млн. оборотов

Расчетная (потребная) динамическая грузоподъемность

= ⋅

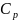где p – показатель степени, который для шарикоподшипников принимается p = 3, для роликоподшипников p = 3,33.

Коэффициент долговечности a₁. Принимаем коэффициент долговечности a₁ = 1 при коэффициенте надежности P(t) = 0,9. Определяем обобщенный коэффициент совместного влияния качества металла a₂₃ примем среднее значение из рекомендуемого диапазона a₂₃ = 0,75.

= 1470,03 ⋅ = 12368,88 H

Должно выполняться условие

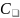
Данное условие выполняется: =12,3 кН ≤ C = 26,9 кН, т. е. расчетная динамическая грузоподъемность не превышает базовую (паспортную), значит, динамическая грузоподъемность подшипника обеспечена.

Коэффициенты радиальной и осевой статических сил для рассматриваемого примера X₀ = 0,5, Y₀ = 0,47.

Определяем эквивалентную статическую нагрузку с учетом большей нагруженности левой опоры А. Используем максимальные, а не средние значения реакций.

= ⋅ + ⋅

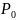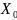= 0,5 ⋅ 1413,48 + 0,47 ⋅ 1047,73 = 1199,17 H

При этом должно выполняться условие P₀ ≥ R_А, т. е. для дальнейших расчетов необходимо выбрать из двух значений P₀ и R_A максимальное. Данное условие не выполняется, поэтому принимаем P₀ = R_А = 1413,48 H.

С учетом трехкратной перегрузки P_0П = 3 ⋅ P₀ = 3 ⋅ 1413,48 = 4240,44 H.

Должно выполняться условие

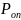
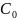
Условие выполняется: 4,24 кН ≤ 20,4 кН.

Статическая грузоподъемность подшипника обеспечена.