
- •Пояснительная записка
- •Содержание
- •1 Энерго-кинематический расчёт привода
- •2 Проектный расчёт передач редуктора
- •2.1 Выбор материала и определение допускаемых напряжений для червячной передачи.
- •2.2 Проектный расчет червячной передачи
- •2.3 Проверочный расчет червячной передачи
- •2.4 Расчет геометрий червячной передачи
- •2.5 Тепловой расчет червячного редуктора
- •3 Расчет открытой передачи червячного редуктора
- •4. Расчет валов привода
- •4.1 Проектный расчет всех валов привода
- •4.2 Проверочный расчет тихоходного вала редуктора на усталостную выносливость
- •4.3 Проверочный расчет тихоходного вала редуктора на статическую перегрузку и жесткость
- •5. Подбор подшипников для валов привода
- •5.1 Предварительный выбор подшипников качения для всех валов привода и его обоснование
- •5.2 Проверочный расчет подшипников тихоходного вала на динамическую и статическую грузоподъёмность
- •6. Расчет шпоночных соединений в приводе
- •7. Выбор муфт
- •8. Обоснование и выбор смазочных материалов
- •9. Техника безопасности и экологичность проекта.
- •Заключение
- •Список использованных источников
2.3 Проверочный расчет червячной передачи
Проверяем прочность зубьев по контактным напряжениям по формуле:
= 1,18 ⋅
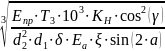
где T3
‒ момент на валу червячного колеса,
Н·м; KН
− коэффициент расчетной нагрузки; δ −
угол обхвата червяка колесом, δ = 50º =
0,873 рад; α ε ‒ коэффициент торцового
перекрытия, α ε = 1,8…2,2. Принимаем
 1,8
(худший случай); ξ ‒ коэффициент,
учитывающий уменьшение длины контактной
линии в связи с тем, что соприкосновение
осуществляется не по полной дуге обхвата,
ξ = 0,75; α ‒ угол профиля зуба (α = 20°).
1,8
(худший случай); ξ ‒ коэффициент,
учитывающий уменьшение длины контактной
линии в связи с тем, что соприкосновение
осуществляется не по полной дуге обхвата,
ξ = 0,75; α ‒ угол профиля зуба (α = 20°).
Коэффициент расчетной нагрузки:
 =
=
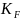 =
=
 ⋅
⋅

где ‒ коэффициент динамической нагрузки; ‒ коэффициент концентрации нагрузки.
Коэффициент динамической нагрузки равен: при vск ≤ 3 м/с = 1; при vск > 3 м/с = 1…1,3. Принимаем Kυ = 1,3.
Коэффициент концентрации нагрузки определяем по формуле:
= 1 +
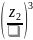 ⋅
(1 – X)
⋅
(1 – X)
где ‒ коэффициент деформации червяка, = 70; X – коэффициент режима нагрузки передачи, X = 0,5.
= 1 +
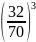 ⋅
(1 – 0,5) = 1,047
⋅
(1 – 0,5) = 1,047
В рассматриваемом случае коэффициент смещения отличен от нуля (x = ‒0,16), поэтому значение = 1,8 принято из рекомендуемого диапазона 1,8…2,2 как худший случай.
По формуле:
= = 1,3 ⋅ 1,047 = 1,3611
Контактные напряжения по формуле:
= 1,18 ⋅
 = 118,91 МПа.
= 118,91 МПа.
< [ ] = 119,42 МПа.
Контактная прочность передачи обеспечена.
Недогрузка составляет:
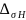 =
=
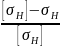 ⋅
100%
⋅
100%
=
 ⋅
100% = 0,42
⋅
100% = 0,42
что менее 20 % и является допустимым. Напомним, что перегрузка, в случае ее возникновения, не должна превышать 5 %.
Проверяем прочность зуба по напряжениям изгиба по формуле:
= 0,74 ⋅
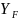 ⋅
⋅
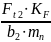
где
 ‒ окружное усилие на колесе, Н;
‒ коэффициент расчётной нагрузки. По
формуле
= 1,3611;
‒ коэффициент формы зуба, зависящий от
эквивалентного числа зубьев zv;
‒ окружное усилие на колесе, Н;
‒ коэффициент расчётной нагрузки. По
формуле
= 1,3611;
‒ коэффициент формы зуба, зависящий от
эквивалентного числа зубьев zv;
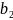 – ширина зубчатого венца червячного
колеса, мм;
– ширина зубчатого венца червячного
колеса, мм;
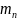 ‒ модуль в нормальном сечении, мм.
‒ модуль в нормальном сечении, мм.
Эквивалентное число зубьев колеса:
 =
=
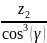
=
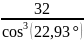 = 40,96
= 40,96
Интерполируя данные, получаем:
= 1,55 −
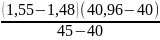 = 0,873
= 0,873
Окружное усилие
на червяке
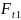 ,
равное осевому усилию на червячном
колесе
,
равное осевому усилию на червячном
колесе
 ,
,
=
=
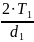
=
=
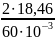 =
615,33 H
=
615,33 H
Окружное
усилие на червячном колесе
, равное осевому усилию на червяке
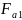 ,
,
=
=
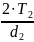
=
=
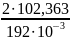 =
1066,28 H
=
1066,28 H
Радиальное усилие:
 =
=
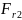 =
⋅
tg(α)
=
⋅
tg(α)
=
= 1066,28 ⋅
tg(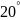 )
= 388,094 H
)
= 388,094 H
Ширину червячного колеса принимаем:
= 0,315 ⋅
= 0,315 ⋅ 125 = 39,375 мм
Нормальный модуль :
= m
⋅
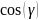
= 6 ⋅
 = 5,52 мм
= 5,52 мм
Тогда по формуле:
= 0,74 ⋅
1,536 ⋅
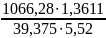 = 7,59 МПа
[
]
= 38,96 МПа
= 7,59 МПа
[
]
= 38,96 МПа
Условие изгибной прочности выполняется.
Назначаем 7-ю степень точности.
2.4 Расчет геометрий червячной передачи
Диаметры вершин и впадин червяка:
 =
=
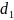 + 2 ⋅
m
+ 2 ⋅
m
= 60 + 2 ⋅ 6 = 72 мм
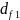 =
– 2,4 ⋅
m
=
– 2,4 ⋅
m
= 60 – 2,4 ⋅ 6 = 45,6 мм
Диаметры вершин и впадин червячного колеса:
 = (
+ 2 + 2 ⋅
x)
⋅
m
= (
+ 2 + 2 ⋅
x)
⋅
m
= (32+ 2 + 2 ⋅ (-0,16)) ⋅ 6 = 202,08 мм
= ( − 2 + 2 ⋅ x) ⋅ m
= (32 – 2,4 + 2 ⋅ (-0,16)) ⋅ 6 = 175,68 мм
Длину нарезанной
части червяка
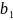 определяем:
определяем:
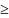 (9,5 + 0,09 ⋅
)
⋅
m
= (9,5 + 0,09 ⋅
32) ⋅
6 = 74,28 мм
(9,5 + 0,09 ⋅
)
⋅
m
= (9,5 + 0,09 ⋅
32) ⋅
6 = 74,28 мм
Принимаем = 75 мм.
Диаметр колеса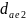 определяем по формуле:
определяем по формуле:
= 208,08 мм + 2 ⋅ m = 175,68 + 2 ⋅ 6 = 214,08 мм
