
- •Пояснительная записка
- •Содержание
- •1 Энерго-кинематический расчёт привода
- •2 Проектный расчёт передач редуктора
- •2.1 Выбор материала и определение допускаемых напряжений для червячной передачи.
- •2.2 Проектный расчет червячной передачи
- •2.3 Проверочный расчет червячной передачи
- •2.4 Расчет геометрий червячной передачи
- •2.5 Тепловой расчет червячного редуктора
- •3 Расчет открытой передачи
- •3.1 Проверочный расчет открытой передачи
- •4. Расчет валов привода
- •4.1 Проектный расчет всех валов привода
- •4.2 Проверочный расчет тихоходного вала редуктора на усталостную выносливость
- •4.3 Проверочный расчет тихоходного вала редуктора на статическую перегрузку и жесткость
- •5. Подбор подшипников для валов привода
- •5.1 Предварительный выбор подшипников качения для всех валов привода и его обоснование
- •5.2 Проверочный расчет подшипников тихоходного вала на динамическую и статическую грузоподъёмность
- •6. Расчет шпоночных соединений в приводе
- •7. Выбор муфт
- •8. Обоснование и выбор смазочных материалов
- •9. Техника безопасности и экологичность проекта.
- •Заключение
- •Список использованных источников
2.4 Расчет геометрий червячной передачи
Диаметры вершин и впадин червяка:
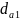 =
=
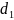 + 2 ⋅
m; (2.31)
+ 2 ⋅
m; (2.31)
= 60 + 2 ⋅ 6 = 72 мм;
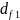 =
– 2,4 ⋅
m; (2.32)
=
– 2,4 ⋅
m; (2.32)
= 60 – 2,4 ⋅ 6 = 45,6 мм.
Диаметры вершин и впадин червячного колеса:
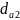 = (
+ 2 + 2 ⋅
x)
⋅
m; (2.33)
= (
+ 2 + 2 ⋅
x)
⋅
m; (2.33)
= (32+ 2 + 2 ⋅ (-0,16)) ⋅ 6 = 202,08 мм;
= ( − 2 + 2 ⋅ x) ⋅ m; (2.34)
= (32 – 2,4 + 2 ⋅ (-0,16)) ⋅ 6 = 175,68 мм.
Длину нарезанной
части червяка
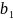 определяем:
определяем:
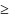 (9,5 + 0,09 ⋅
)
⋅
m
= (9,5 + 0,09 ⋅
32) ⋅
6 = 74,28 мм.
(9,5 + 0,09 ⋅
)
⋅
m
= (9,5 + 0,09 ⋅
32) ⋅
6 = 74,28 мм.
Принимаем = 75 мм.
Диаметр колеса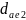 определяем по формуле:
определяем по формуле:
= 208,08 мм + 2 ⋅ m = 175,68 + 2 ⋅ 6 = 214,08 мм.
2.5 Тепловой расчет червячного редуктора
При vск = 16,59 м/с принимаем коэффициент трения ориентировочно f = 0,017.
Определяем угол трения φ по формуле:
φ = arctg (f); (2.35)
φ = arctg (0,017) = 0,017 рад.
Уточняем КПД червячной передачи по формуле:
η
=
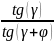 ; (2.36)
; (2.36)
η
=
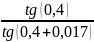 = 0,959.
= 0,959.
Количество теплоты, выделяющееся в передаче в секунду (тепловая мощность), определяем по формуле:
W
=
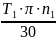 ⋅
(1 – η); (2.37)
⋅
(1 – η); (2.37)
W
=
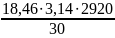 ⋅
(1 – 0,959) = 231,31 Вт.
⋅
(1 – 0,959) = 231,31 Вт.
Мощность теплоотдачи:
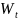 = K
⋅
(
= K
⋅
( )
⋅ A
; (2.38)
)
⋅ A
; (2.38)
= 9 ⋅ (75 – 20) ⋅ 0,35 = 173,25 Вт.
где K ‒ коэффициент теплоотдачи. В закрытых помещениях при отсутствии вентиляции K = 8…10 Вт/(м2 ·°С). В помещениях с интенсивной вентиляцией K = 14…17 Вт/(м2 · °С). Принимаем K = 9; t1 ‒ внутренняя температура редуктора (температура масла), °С. Выбираем индустриальное редукторное масло, t1 = 60…90 °С. Принимаем t1 = 75 °С; t0 ‒ температура окружающей среды, °С. Считаем, что средняя температура помещения (отапливаемого зимой) t0 = 20 °С; А ‒ площадь поверхности охлаждения, м2. Принимаем А = 0,78 м2.
В рассматриваемом случае применяем охлаждающие ребра. Тогда площадь поверхности охлаждения
A = A0 + kp ⋅ Ap; (2.39)
A = 0,35 + 1 ⋅ 0,14 = 0,49 м2.
где kp ‒ коэффициент охлаждения с помощью ребер; kp = 1 – для вертикальных ребер, kp = 0,5 ‒ для горизонтальных. Принимаем kp = 1; Ap ‒ площадь ребер, м2. Принимаем Ap = 0,4 ⋅ A0 = 0,4 ⋅ 0,35 = 0,14 м2.
Дополнительно устанавливаем интенсивную вентиляцию в помещении (K = 15). Тогда по формуле:
= K ⋅ ( ) ⋅ A = 15 ⋅ (75 – 20) ⋅ 0,49 = 404,25 Вт.
Мощность отводимая (теплоотдачи) должна быть равной или больше мощности выделяемой. Это условие теплового баланса. В рассматриваемом случае должно выполняться неравенство:
W
Условие теплового баланса выполняется.
3 Расчет открытой передачи
Допускаемые контактные напряжения определяем по формуле:
[
]
=
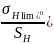 ⋅
⋅
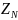 ; (3.1)
; (3.1)
где
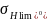 – предел контактной выносливости
зубьев, МПа;
– коэффициент долговечности;
– предел контактной выносливости
зубьев, МПа;
– коэффициент долговечности;
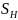 – коэффициент безопасности.
– коэффициент безопасности.
Коэффициент
безопасности
принимаем равным 1,2 при поверхностном
упрочнении зубьев (цементация,
азотирование и др.) и 1,1 ‒ в других
случаях. В данном примере
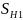 = 1,2,
= 1,2,
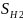 = 1,1.
= 1,1.
Предел контактной выносливости 0 H lim определяем:
Для шестерни
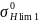 = 880 МПа.
= 880 МПа.
Предел контактной выносливости для колеса
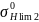 = 1,8 ⋅
= 1,8 ⋅
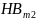 + 65; (3.2)
+ 65; (3.2)
где – среднее значение твердости поверхности колеса (230…260 HB) в единицах Бринелля, = 245.
Базовое число циклов для колеса NHG2 можно найти по формуле для зубчатых колес с твердостью поверхности менее 350 HB:
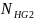 = 30 ⋅
= 30 ⋅
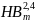 ; (3.3)
; (3.3)
= 30 ⋅ 5402,4 = 1,6 ⋅ 107.
Базовое число циклов для шестерни NHG1 определяем аналогично, предварительно найдя среднее значение в единицах по Рокуэллу:
HRCm1
=
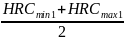 ;
(3.4)
;
(3.4)
HRCm1
=
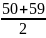 = 54,5.
= 54,5.
Тогда по формуле:
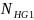 = 30 ⋅
; (3.5)
= 30 ⋅
; (3.5)
= 30 ⋅ 5402,4 = 10,8 ⋅ 107.
Ресурс работы передачи в часах:
= L ⋅ ⋅ ⋅ 8; (3.6)
где ‒ количество рабочих дней в году (при пятидневной рабочей неделе ≈ 255, при шестидневной ‒ ≈ 305); – количество смен, = 2 (согласно исходным данным); L – срок службы (ресурс), L = 5 лет (по исходным данным).
= 5 ⋅ 255 ⋅ 2 ⋅ 8 = 20400 ч.
Эквивалентное число циклов для шестерни:
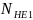 =
⋅
60 ⋅
c
⋅
⋅
; (3.7)
=
⋅
60 ⋅
c
⋅
⋅
; (3.7)
где – коэффициент режима работы. В рассматриваемом случае = 0,25, т. к. задан средний равновероятный режим работы; с – количество колес, находящихся в зацеплении с данным колесом (шестерней), с = 1.
= 0,25 ⋅ 60 ⋅ 1 ⋅ 365 ⋅ 20400 = 11,17 ⋅ 107.
Для колеса
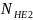 =
⋅
60 ⋅
c
⋅
⋅
; (3.8)
=
⋅
60 ⋅
c
⋅
⋅
; (3.8)
= 0,25 ⋅ 60 ⋅ 1 ⋅ 98,79 ⋅ 20400 = 3,02 ⋅ 107.
Коэффициент долговечности:
=
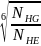 ; (3.9)
; (3.9)
Вычисляем коэффициенты долговечности по формуле для шестерни и колеса соответственно:
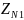 =
=
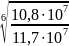 = 1;
= 1;
=
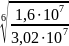 = 1.
= 1.
Допускаемые контактные напряжения определяем по формуле для шестерни и колеса соответственно:
[
]1
=
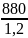 ⋅
1 = 733,3 МПа;
⋅
1 = 733,3 МПа;
[
]2
=
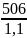 ⋅
1 = 460 МПа.
⋅
1 = 460 МПа.
Находим среднее допускаемое напряжение:
 =
=
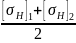 ; (3.10)
; (3.10)
=
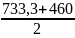 = 596,65 МПа.
= 596,65 МПа.
Предельные значения
допускаемых контактных напряжений
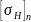
1,25 ⋅
1,25 ⋅
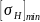 – для цилиндрических передач.
– для цилиндрических передач.
1,25 ⋅ ; (3.11)
1,25 ⋅ 460 = 575 МПа.
Окончательно
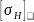 = 575 МПа.
= 575 МПа.
У открытых (работающих без корпуса) цилиндрических зубчатых передач основным прочностным критерием является изгибная прочность.
Допускаемые напряжения изгиба определяем по формуле:
[
]
=
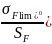 ⋅
⋅
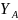 ⋅
⋅
 ; (3.12)
; (3.12)
где
 –
предел выносливости зубьев по напряжениям
изгиба, МПа;
–
предел выносливости зубьев по напряжениям
изгиба, МПа;
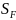 – коэффициент безопасности;
– коэффициент, учитывающий влияние
двухстороннего приложения нагрузки
(для нереверсивных передач
= 1, для реверсивных ‒
= 0,7…0,8, причем большие значения для
колес с HB > 350);
– коэффициент долговечности.
– коэффициент безопасности;
– коэффициент, учитывающий влияние
двухстороннего приложения нагрузки
(для нереверсивных передач
= 1, для реверсивных ‒
= 0,7…0,8, причем большие значения для
колес с HB > 350);
– коэффициент долговечности.
Предел выносливости по напряжениям изгиба можно приближенно оценивать:
 = 12 ⋅
HRCс.ср1
+ 300; (3.13)
= 12 ⋅
HRCс.ср1
+ 300; (3.13)
где HRCс.ср1 – средняя твердость сердцевины шестерни. Она задается при назначении термообработки. Если термообработка производится по всему объему детали (нормализация, улучшение, объемная закалка), то твердость сердцевины равна твердости поверхности.
В рассматриваемом случае твердость сердцевины шестерни была задана 26…30 HRC.
HRCс.ср
=
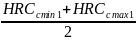 ; (3.14)
; (3.14)
HRCс.ср
=
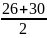 =
28.
=
28.
Тогда
= 12 ⋅ 28 + 300 = 636 МПа.
У колеса термообработка (улучшение) производится по всему объему, поэтому твердость поверхности зубьев и сердцевины будет одинаковой.
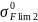 = 1,8 ⋅
HBmc2; (3.15)
= 1,8 ⋅
HBmc2; (3.15)
где HBmc2 – среднее значение твердости сердцевины колеса (230…260 HB) в единицах Бринелля, HBmc2 = 245. HBmc2 = HBm2, т. к. у колеса термообработка по объему (улучшение) и твердость поверхности равна твердости сердцевины.
= 1,8 ⋅ 245 = 441 МПа.
Эквивалентное число циклов перемены напряжений изгиба для шестерни
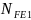 =
=
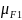 ⋅
60 ⋅
c
⋅
⋅
; (3.16)
⋅
60 ⋅
c
⋅
⋅
; (3.16)
где
– коэффициент режима работы для шестерни
при действии напряжений изгиба. В данном
примере
= 0,1 – для шестерни,
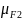 = 0,143 – для колеса.
= 0,143 – для колеса.
= 0,1 ⋅ 60 ⋅ 1 ⋅ 365 ⋅ 20400 = 4,46 ⋅ .
Эквивалентное число циклов для колеса
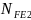 =
⋅
60 ⋅
c
⋅
⋅
; (3.17)
=
⋅
60 ⋅
c
⋅
⋅
; (3.17)
= 0,143 ⋅ 60 ⋅ 1 ⋅ 98,79 ⋅ 20400 = 1,73 ⋅ .
Коэффициент долговечности определяем по формуле:
=
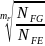 ; (3.18)
; (3.18)
где
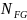 – базовое число циклов (для всех сталей
= 4·106
);
– эквивалентное число циклов;
– базовое число циклов (для всех сталей
= 4·106
);
– эквивалентное число циклов;
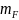 – показатель степени, зависящий от
вида термообработки (определяется по
табл. 2.5). В рассматриваемом примере для
шестерни
= 9 и для колеса
= 6.
– показатель степени, зависящий от
вида термообработки (определяется по
табл. 2.5). В рассматриваемом примере для
шестерни
= 9 и для колеса
= 6.
Коэффициенты долговечности по формуле для шестерни и колеса соответственно
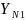 =
=
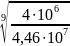 = 1;
= 1;
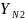 =
=
 = 1.
= 1.
Для шестерни и колеса коэффициент, учитывающий влияние двухстороннего приложения нагрузки, YA 1, т. к. передача нереверсивная.
При нормализации, улучшении, объемной закалке, закалке ТВЧ и азотировании коэффициент безопасности SF принимают равным 1,75. При применении цементации и нитроцементации с закалкой коэффициент SF = 1,55. Таким образом, для колеса SF2 75,1 , для шестерни SF1 1,75 .
Допускаемые напряжения изгиба для шестерни и колеса определяем отдельно по формуле:
[
]1
=
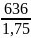 ⋅
1 ⋅
1 = 363 Мпа;
⋅
1 ⋅
1 = 363 Мпа;
[
]2
=
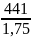 ⋅
1 ⋅
1 = 252 Мпа.
⋅
1 ⋅
1 = 252 Мпа.
Коэффициент распределения нагрузки между зубьями находим по формуле:
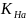 = 1 + C
⋅
(
= 1 + C
⋅
(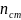 – 5)
– 5)
 ; (3.19)
; (3.19)
где С – коэффициент твердости и типа зубьев. С = 0,06 – для прямозубых передач, С = 0,15 ‒ для косозубых передач при твердости зубьев колеса и шестерни более 350 HB, С = 0,25 ‒ если твердость зубьев колеса меньше либо равна 350 HB;
‒ степень точности изготовления колес, = 5…9; [KHα] ‒ допускаемое значение коэффициента . = 1,25 ‒ для прямозубых передач, = 1,6 ‒ для косозубых
= 1 + 0,25 ⋅ (7– 5) = 1,5 1,6.
Коэффициент формы
зуба
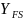 выбираем по графику при коэффициентах
смещения x1
= x2
= 0 в зависимости от эквивалентного
числа зубьев zv
шестерни и колеса.
выбираем по графику при коэффициентах
смещения x1
= x2
= 0 в зависимости от эквивалентного
числа зубьев zv
шестерни и колеса.
Если межосевое расстояние (или габариты) передачи изначально не задано, можно принимать z1 ≥ 21 ‒ для прямозубых передач и z1 ≥ 17 ‒ для косозубых. Находим коэффициент ψm = 25.
=
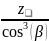 ; (3.20)
; (3.20)
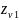 =
=
 = 21;
= 21;
 =
=
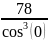 = 78.
= 78.
При нулевом
суммарном смещении для шестерни YFS1
= 4,1, для колеса YFS2
= 3,75. Для шестерни и для колеса находим
отношение
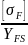 :
:
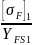 =
=
 = 88,53;
= 88,53;
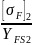 =
=
 = 67,2.
= 67,2.
Дальнейший расчет ведем по колесу, т. к. данное соотношение меньше. То есть принимаем [ ] = [ ]2 = 252 МПа, YFS = YFS2 = 3,75.
Коэффициент ширины колеса относительно делительного диаметра:
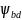 = 0,5 ⋅
= 0,5 ⋅
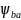 ⋅
(u
⋅
(u
 1); (3.21)
1); (3.21)
= 0,5 ⋅ 0,3 ⋅ (3,7 + 1) = 0,705.
Коэффициент концентрации нагрузки KFβ определяем по графикам в зависимости от ψbd.
KFβ = 1,45.
Определяем модуль m, мм, для прямозубых передач по формуле:
m
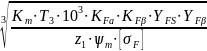 ; (3.22)
; (3.22)
где T1 ‒ момент на шестерне открытой передачи, Н·м; Km ‒ коэффициент, учитывающий тип передачи: Km = 2 ‒ для косозубых, Km = 3 ‒ для прямозубых колес. Из двух отношений [σF]1/YFS1 и [σF]2/YFS2 выбирается минимальное [σF]/YFS, его составляющие подставляются в формулу для вычисления модуля. При этом допускаемые напряжения подставляются в мегапаскалях (МПа).
m
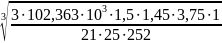 = 2,66 мм.
= 2,66 мм.
Принимаем m = 2,75 мм.
Делительный диаметр шестерни для стальных зубчатых колес определяем по формуле из ГОСТ 21354‒87:
=
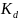 ⋅
⋅
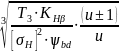 ; (3.23)
; (3.23)
где Kd – вспомогательный коэффициент, Kd = 680 Мпа1/3 ‒ для косозубых колес, Kd = 780 Мпа1/3 ‒ для прямозубых; u – передаточное число передачи (равно по модулю заданному передаточному отношению), u = i = 3,7; T3 – момент на быстроходном валу передачи (на валу, где расположена шестерня), Н. м; KHβ – коэффициент концентрации нагрузки; ψbd – коэффициент ширины колеса относительно делительного диаметра.
= 680 ⋅
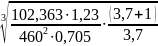 = 69,59 мм.
= 69,59 мм.
Определяем ширину зубчатых колес:
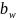 =
⋅
; (3.24)
=
⋅
; (3.24)
= 69,59 ⋅ 0,705 = 49,06 мм.
Округляем данное значение в большую сторону и принимаем ширину колеса bw2 = bw = 49 мм. Ширину шестерни можно увеличить на 5…10 мм. Принимаем bw1 = 54 мм.
Модуль передачи (в нормальном сечении) определяем по формуле:
=
 ; (3.25)
; (3.25)
=
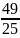 = 1,96 мм.
= 1,96 мм.
Принимаем = 2,5 мм.
Определяем геометрические параметры передачи, необходимые для проверочного расчета. Делительные диаметры шестерни и колеса:
=
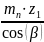 ; (3.26)
; (3.26)
=
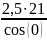 = 52,5 мм;
= 52,5 мм;
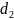 =
=
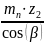 ; (3.27)
; (3.27)
=
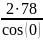 = 195 мм.
= 195 мм.
Предварительно определяем межосевое расстояние:
=
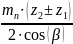 ; (3.28)
; (3.28)
=
 = 123,75 мм.
= 123,75 мм.
