Алгебра_кортежей

снеоднозначным результатом в атрибуте W. Однако эту неоднозначность можно устранить, если использовать правило приоритета. Приоритет здесь определяется порядком расположения C-кортежей в R: первый полученный непустой результат пересечения является окончательным. С учетом этого для заданного входа получается результат W = c.

Из приведенного примера видно, что на основе АК можно создавать "прозрачные" и сравнительно простые в реализации интерпретаторы экспертных систем и к тому же проверять корректность правил на этапе проектирования системы. В последние годы по мере усложнения прикладных ЭС стало ясно, что для их разработки явно недостаточно средств, которые используются в "интеллектуальных" языках программирования (Пролог, Лисп и др.). Поэтому разработчики вынуждены переходить на программирование ЭС

спомощью языков высокого уровня, таких как C++, Object Pascal, Perl и т.д., где используются и средства управления базами данных, и методы объектноориентированного программирования. Вызвано это необходимостью совмещения структур данных и знаний. Использование АК позволяет более просто решить эту проблему, так как в ней данные и знания органично выражаются в одних и тех же структурах и обеспечены соответствующими алгоритмами.

Семантические сети. Покажем, как в АК осуществляется вывод на семантических сетях [Kulik, 2010]. Каждую семантическую сеть можно представить как совокупность бинарных отношений. Правила вывода в семантической сети записываются в виде продукций, в левой части которых содержится какой-либо фрагмент семантической сети (соединения или композиции некоторых из исходных отношений), а в правой части – фрагмент, заменяющий левую часть или добавляемый в семантическую сеть как новое отношение при срабатывании правила. Например, отношение "быть внуком" появляется в результате композиции отношения "быть сыном" с самим собой.

При реализации продукционного правила средствами АК в общем случае необходимо выполнить следующую последовательность шагов:

1)получить соединение или композицию отношений, стоящих в левой части правила;

2)исключить из получившегося отношения P все кортежи, не удовлетворяющие заданным ограничениям;

202

3)получить соединение (композицию) отношений T, стоящих в правой части продукции, при необходимости с учетом множества кортежей, получившихся при вычислении левой части правила;

4)если в правиле предусматривается замена левой части на правую, то из исходной базы знаний удалить все связи, содержащиеся в P;

5)добавить в базу знаний все связи из отношения T.

Рассмотрим пример из книги Д.А. Поспелова [Поспелов, 1989].

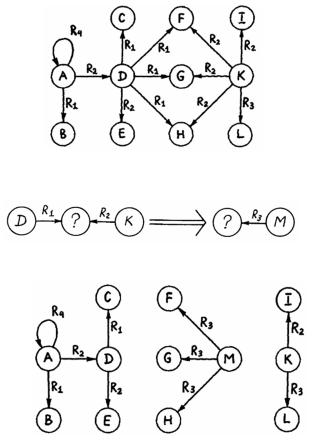
Исходная семантическая сеть изображена на рис. 5.6, правило вывода на этой сети на рис. 5.7, а результат применения правила – на рис. 5.8.

Рис. 5.6. Исходная семантическая сеть

Рис. 5.7. Продукция

Рис. 5.8. Результат применения продукции

Сначала выразим в структурах АК исходную сеть. Ее на языке АК можно записать в виде совокупности C-систем и С-кортежей:

R3[VY] = [{K} {L}]; R4[ZW] = [{A} {A}].

В левой части продукции предусматривается соединение отношений R1 и

203

отношения, а другие слоты. С точки зрения АК атрибуты, представленные такими усложненными слотами, имеют в качестве доменов не множества с простыми элементами, а многоместные отношения, элементами которых являются кортежи. Такие разветвленные фреймы также представимы в структурах АК. Иногда в качестве слотов используются правила – ранее было показано, что их также можно выразить на языке АК.

Выше было показано, как с помощью АК-объектов могут быть отображены основные модели представления знаний, применяемые в системах искусственного интеллекта. Далее в главе демонстрируются возможные применения АK для задач искусственного интеллекта [Зуенко, 2010 b].

5.3.2. АК и неоднородные семантические сети

Понятие неоднородной семантической сети введено Г. С. Осиповым для описания плохо структурированных предметных областей, где знания об индивидах и их взаимосвязях не имеют завершенного вида [Осипов, 2009].

Неоднородной интенсиональной семантической сетью называют алгебраическую систему

H = <D, N, R, F>,

где D = {D1, D2, …, Dn} – семейство непустых множеств; N N – выделенное подмножество слов конечной длины над заданным алфавитом; R = {R1, R2, …, Rq} – семейство бинарных отношений на N2, F = {f1, f2, …, fm} –

Dk1×Dk2×…×Dkm, а областью ее значений является множество D , т. е. каждому кортежу Dk1×Dk2×…×Dkm функция fi ставит в соответствие некоторый элемент fi( ) из D .

Если каждому n N приписать тип , а также e – некоторое подмножество декартова произведения Dk1×Dk2×…×Dkm (экстенсионал, множество примеров), а затем определить на множестве экстенсионалов E = {ei} отношения Ri* вместо отношений Ri на N2, то полученная конструкция:

H* = <D, E, R*, F>

называется экстенсиональной неоднородной семантической сетью (ЭНС).

205

ЭНС применяются в некоторых методах приобретения знаний, а также при организации правдоподобных рассуждений, в частности, в задачах аргументации [Осипов, 2009]. Процедуры вывода основаны на том, что элементы в парах из Ri* (элементы множества E) сами имеют некоторую внутреннюю структуру, то есть, по существу, тоже являются отношениями, определенными на множествах из D. Это позволяет выразить отношения Ri* через внутреннюю структуру элементов из E, а также выделить следующие классы отношений: a) отношения структурного сходства, b) ассоциативные и каузальные отношения. Далее приведем определения отношений структурного сходства, а затем перепишем условия этих определений на языке АК.

Пусть e1, e2 – произвольная пара отношений из E, , – примеры (в терминах АК – это элементарные кортежи) отношений e1, e2 соответственно. Результатом пересечения будет общий фрагмент слов и , а под записьюпонимается, что слово включено в слово (здесь кортежи рассматриваются как слова некоторого языка, в АК отношение включения для двух кортежей трактуется иначе (см. п. 2.3)).

Определение 5.1. Отношением R1 на E называется такое X E2, что для всякой пары (e1, e2) X имеет место e1, e2, что .

Определение 5.2. Отношением R2 на E называется такое X E2, что для

всякой пары (e1, e2) X имеет место e1, e2, что .

В [Осипов, 2009] дано естественно-языковое описание этих отношений. Так, например, принадлежность пары событий отношению R1 означает, что событие e1 всегда сопровождается событием e2; а R3 – событие e1 иногда

206

сопровождается e1. Там же вводятся специальные диаграммы для наглядного представления таких отношений: каждое отношение ei представляется в виде прямоугольника, по горизонтальной стороне которого откладываются свойства отношения, а по вертикали – множества значений по каждому из свойств или объемы. В частности:

Рис. 5.9. Диаграммы отношений структурного сходства

На языке АК условия, соответствующие введенным определениям и рис. 5.9, примут следующий вид (жирным шрифтом выделены множества нефиктивных атрибутов):

1.Отношения e1 и e2 должны быть представимы в виде C-систем E1[XYZ] (как атрибуты X, так и атрибуты Z могут отсутствовать) и E2[Y], а также удовлетворять соотношению E1[XYZ] G E2[Y].

2.Отношения e1 и e2 должны выражаться как C-системы E1[XY] и E2[YZ], (атрибуты X и атрибуты Z либо одновременно присутствуют в схемах отношений, либо одновременно отсутствуют), и при этом требуется, чтобы E1[Y] E2[Y], где E1[Y], E2[Y] здесь и далее проекции соответствующих отношений на атрибут Y.

3.Отношения e1 и e2 должны записываться в виде C-систем E1[X] и

E2[X], причем E1[X] E2[X] ≠ Ø;

4. Отношения e1 и e2 должны соответствовать C-системам E1[XY] и E2[YZ] (либо атрибуты X, либо атрибуты Z могут отсутствовать), для которых выполняется E1[Y] E2[Y] ≠ Ø.

207

5.Отношения e1 и e2 должны допускать представление в виде C-систем E1[Y] и E2[XYZ] (либо атрибуты X, либо атрибуты Z могут отсутствовать), и удовлетворять требованию E1[Y] E2[Y].

6.Отношения e1 и e2 должны выражаться как C-системы E1[XYZ] (либо атрибуты X, либо атрибуты Z могут отсутствовать) и E2[Y], а также должно соблюдаться E1[Y] E2[Y] ≠ Ø.

При проверке условий 1-6 представление отношений e1 и e2 в виде множеств С-кортежей и применение методов АК, описанных в главах 2 и 3, позволяет существенно снизить трудоемкость операций, производимых над этими отношениями, а также более экономно расходовать память для их хранения.

5.3.3. АК и формальный анализ понятий

В отличие от статистических методов, формальный анализ понятий (ФАП) дает возможность описывать отношения между объектами изучаемых предметных областей в виде решеток формальных понятий [Kuznetsov, 2002].

Формальный контекст – это тройка K = (G, M, I), где G – множество объектов, M – множество признаков, I G×M – отношение обладания признаком. Пара gi, mj I показывает, что объект gi обладает признаком mj. Часто формальный контекст представляют в виде бинарной матрицы, например, такой, как в табл. 5.9.

Определение формального понятия содержит операторы Галуа A’ и B’. Для

A G и B M: A’ = {m M | g A: gIm}, B’= {g G | m B: gIm}. Другими словами, A’ – множество признаков, которыми обладают все объекты из множества A, B’ – множество объектов, которые обладают всеми признаками из множества B.

Таблица 5.9.

208