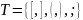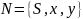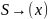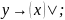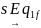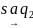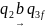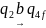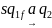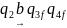- •Двойственная функция.
- •Самодвойственная функция.
- •45. Нормальные алгоритмы Маркова: определение, примеры.
- •46. Определения алгоритма по Тьюрингу, Черчу и Маркову.
- •47. Вычислительная сложность алгоритма: определение. Приведите пример алгоритма, имеющего сложность o(n5).
- •48. Детерминированная и недетерминированная мт. Классы p и np - определение, связь с мт.
- •47. Вычислительная сложность алгоритма: определение. Приведите пример алгоритма, имеющего сложность o(n5).
- •48. Детерминированная и недетерминированная мт. Классы p и np - определение, связь с мт.
- •49. Язык, распознающая грамматика, порождающая грамматика - определения.
48. Детерминированная и недетерминированная мт. Классы p и np - определение, связь с мт.
МТ называется детерминированной, если каждой комбинации состояния и ленточного символа соответствует не более одного правила.
Если существует пара «ленточный символ — состояние», для которой существует 2 и более команд, такая МТ называется недетерминированной.
К классу P относятся алгоритмы, выполняемые не более чем за полиноминальное время, и могут быть реализованы на детерминированной МТ
К классу NP относятся алгоритмы, которые можно за полиномиальное время решить на недетерминированной МТ
49. Язык, распознающая грамматика, порождающая грамматика - определения.
Язык-множество слов корректной структуры(слово-последовательность символов алфавита языка)
Распознающая грамматика-алгоритм распознающий корректность слова, поданного на вход
Порождающая грамматика- алгоритм строящий все корректные слова языка.
50-51. Иерархия Хомского. Пример КЗ-грамматики. Пример КС-грамматики.
Иерархия Хомского — классификация порождающих грамматик по типам правил вывода
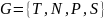 -свободные
грамматики
-свободные
грамматики
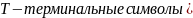
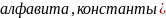
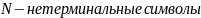
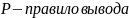
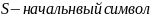
Тип:
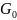 -свободные
грамматики
-свободные
грамматики
Ограничений на правило вывода нет
Тип:
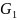 -
контекстно зависимые грамматики
-
контекстно зависимые грамматики
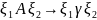 ,
,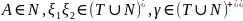
Тип:
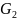 -
контекстно свободные грамматики
-
контекстно свободные грамматики
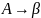 ,
,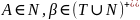
Тип: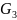 -автоматные(регулярные)
грамматики
-автоматные(регулярные)
грамматики
*леволинейные(леворекурсивные)
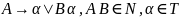
*праволинейные(праворекурсивные)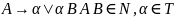
КЗ-грамм |
КС-грамм |
Язык
{
|
Язык
{…
|
52-53. Конечный автомат - определение. Приведите примеры НКА и ДКА.
Конечный автомат — абстрактный автомат, число возможных внутренних состояний которого конечно.
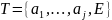
Стартовое
состояние: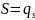
Промежуточные
состояния: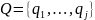
Конечные
состояния: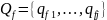
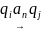
Допустимая
цепочка: последнее состояние

НЕ
допустимая цепочка: последнее состояние
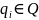 или
чтение не закончилось вовсе
или
чтение не закончилось вовсе
(ДКА)Конечный автомат называют детерминированным если:
1По одному символу осуществляется переход строго в одно состояние
2 Переход по пустому символу запрещен
Недетерминированный конечный автомат (НКА) является обобщением детерминированного.
НKA |
ДКА |
|
|
54-56. Нечеткие множества
Нечетким
множеством 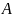 на универсальном множестве
на универсальном множестве  называется совокупность пар (
называется совокупность пар ( 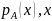 )
где
)
где 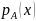 -
степень принадлежности элемента
-
степень принадлежности элемента 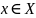 к
нечеткому множеству
.
к
нечеткому множеству
.
Степень принадлежности - это число из диапазона [0, 1]. Чем выше степень принадлежности, тем в большей мерой элемент универсального множества соответствует свойствам нечеткого множества.
Объединение и пересечение.
Объединением
нечетких множеств 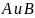 заданных
на
называется нечеткое множество с
функцией принадлежности
заданных
на
называется нечеткое множество с
функцией принадлежности 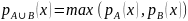 для
всех
.
для
всех
.
Пересечением
нечетких множеств
заданных
на
называется
нечеткое множество с функцией
принадлежности 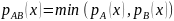 для
всех
.
для
всех
.
Второй вариант определения:
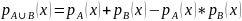
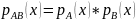
Сумма и произведение.
Треугольной
нормой (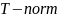 )
называется двуместная действительная
функция
)
называется двуместная действительная
функция 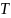 ,
отображающая две функции принадлежности
нормальных нечетких множеств
,
отображающая две функции принадлежности
нормальных нечетких множеств 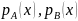 в
одну функцию принадлежности нормального
нечеткого множества.
в
одну функцию принадлежности нормального
нечеткого множества.
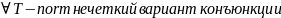
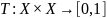
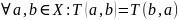 –
симметричность;
–
симметричность;
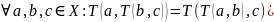 –
ассоциативность.
–
ассоциативность.
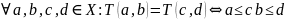 –
монотонность;
–
монотонность;
Поведение
в 1: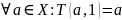
Треугольной
нормой (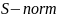 )
называется двуместная действительная
функция
)
называется двуместная действительная
функция 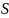 ,
отображающая две функции принадлежности
нормальных нечетких множеств
в
одну функцию принадлежности нормального
нечеткого множества и удовлетворяющая
следующим условиям:
,
отображающая две функции принадлежности
нормальных нечетких множеств
в
одну функцию принадлежности нормального
нечеткого множества и удовлетворяющая
следующим условиям:
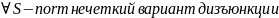
– симметричность;
– ассоциативность.
– монотонность;
Поведение
в 0: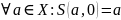
Дополнение и включение
Дополнением
нечеткого множества
заданного
на
называется
нечеткое множество 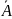 с
функцией принадлежности
с
функцией принадлежности 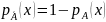 для
всех
для
всех
Включение
 нечеткого множества заданного
на
называется
нечеткое множество
с
функцией принадлежности
нечеткого множества заданного
на
называется
нечеткое множество
с
функцией принадлежности 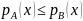 для
всех
для
всех

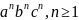 }
}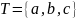
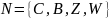
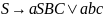
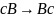
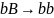
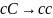
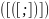 …}
…}