
- •Содержание
- •Введение
- •1 Синтез и анализ механизма
- •1.1 Структурный анализ механизма
- •1.2 Определение скоростей
- •1.3 Определение ускорений
- •2.3 Расчет диады 4-5
- •2.4 Расчет диады 2-3
- •2.5 Расчет кривошипа 1
- •3.2 Синтез и анализ планетарного редуктора
- •3.3 Определение частот вращения зубчатых колес аналитическим и графическим методами
- •4 Синтез и анализ кулачкового механизма
- •4.1 Построение кинематических диаграмм и определение масштабных коэффициентов
- •4.2 Определение минимального радиуса кулачка
- •4.3 Построение профиля кулачка
- •4.4 Определение максимальной линейной скорости и ускорения толкателя
- •Заключение
- •Список литературы
3.2 Синтез и анализ планетарного редуктора
Исходные данные:
Модуль
Частота вращения вала двигателя

Частота вращения кривошипа

Числа зубьев

Номер схемы редуктора
 .
.
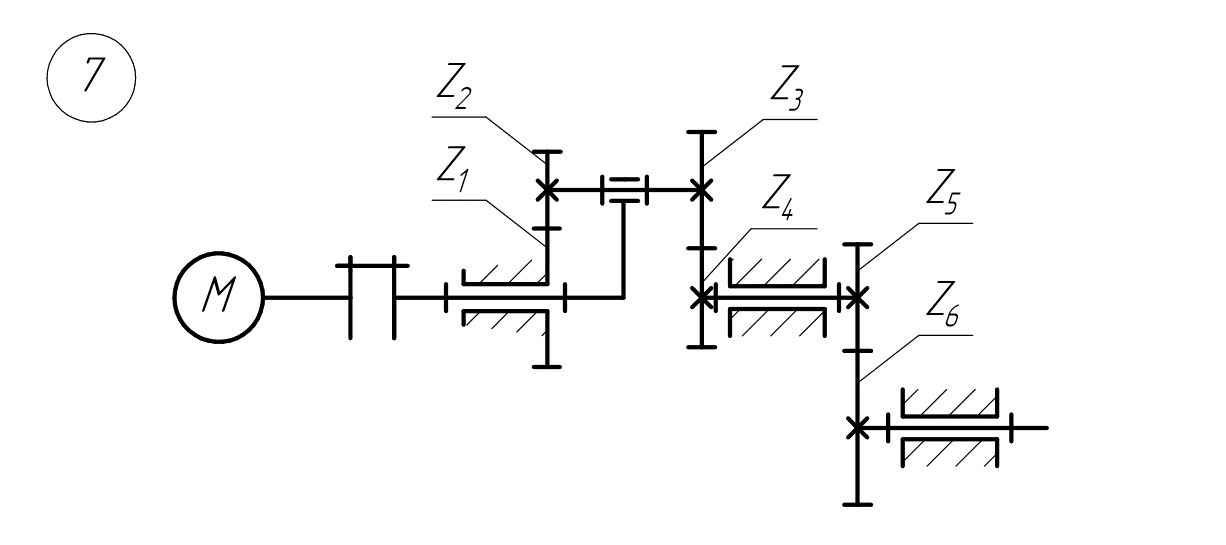
Рисунок 3.1 – Редуктор
Передаточное отношение простой передачи

Общее передаточное отношение редуктора

Передаточное отношение планетарной передачи

Формула Виллиса для планетарной передачи

Принимаем

Подбор чисел зубьев планетарной передачи:

Условие соосности для данной передачи:



Принимаем числа зубьев колёс, равных: z1=111; z2=33; z3=32; z4=112.
По принятым числам зубьев определяем диаметры колёс:

Принимаем масштабный коэффициент построения кинематической схемы редуктора:

Скорость точки А зубчатого колеса 1:

Строим планы скоростей. Масштабный коэффициент плана скоростей:

Строим план частот вращения звеньев редуктора. Масштабный коэффициент плана частот вращения звеньев редуктора:

3.3 Определение частот вращения зубчатых колес аналитическим и графическим методами
Значения частот, полученные аналитическим методом:





Значения частот, полученных графическим методом:

Определяем погрешность расчётов:



4 Синтез и анализ кулачкового механизма
Исходные данные:
а) диаграмма движения выходного звена
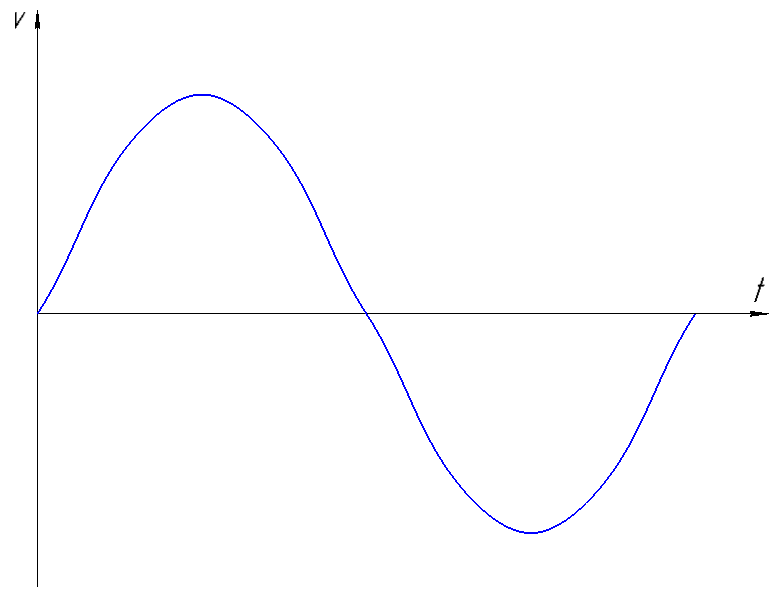
б) частота вращения кривошипа nкр=9 мин-1;
в) ход толкателя h=40 мм;
г) допускаемый угол давления α=30 град;
д) рабочий угол кулачка φр=110 град;
е) кулачковый механизм с роликовым толкателем;
4.1 Построение кинематических диаграмм и определение масштабных коэффициентов
По заданному графику скорости толкателя v = f(t), графическим интегрированием по методу хорд и дифференцированием по методу хорд получаю графики ускорения и перемещения роликового толкателя. Графики a = f(v), a = f(s), v = f(s) получаем методом исключения общего переменного.
База интегрирования:

Масштабный коэффициент перемещения толкателя:

где ysmax – максимальное значение ординаты графика s=f(t), мм.
Масштабный коэффициент времени:

где nкул – частота
вращения кулачка:

 =180
мм – длина отрезка на оси абсцисс
графика, изображающая время поворота
кулачка на рабочий угол.
=180
мм – длина отрезка на оси абсцисс
графика, изображающая время поворота
кулачка на рабочий угол.
Масштабный коэффициент скорости толкателя:

Масштабный коэффициент ускорения толкателя:

4.2 Определение минимального радиуса кулачка
Принимаю масштабный коэффициент
построения

По оси ординат графика v’ – s’в масштабе K’S откладываем величину перемещения толкателя y’Smax, мм:

Находим отрезки в масштабе K’S, изображающие перемещение толкателя в каждом положении графически.
Отрезки приведенной скорости толкателя определим графически, для чего находим максимальное значение приведенной скорости:

где yvmax – максимальное значение ординаты графика v = f(t), мм,
ωкул
– угловая скорость кулачка,

Для остальных положений отрезки приведенной скорости определяются графически.
Значение минимального радиуса центрового профиля кулачка:

Радиус ролика:

Тогда истинное значение минимального радиуса кулачка:

