
- •1. Кинематический анализ и синтез рычажного механизма
- •1.1 Структурный анализ механизма
- •1.2 Построение планов положения механизмов
- •1.4 Построение планов ускорений механизма
- •1.5 Определение угловых скоростей и ускорений для первого положения механизма
- •2.8 Расчет приведенного момента инерции
- •3. Расчёт и проектирование зубчатого механизма
- •3.1 Расчет геометрических параметров и построение картины эвольвентного зацепления
- •3.2 Синтез и анализ комбинированного зубчатого механизма
- •3.3 Построение плана скоростей
- •3.4 Построение плана частот вращения
- •4 Синтез и анализ кулачкового механизма
- •4.1 Построение кинематических диаграмм и определение масштабных коэффициентов
- •4.2 Определение минимального радиуса кулачка
- •4.3 Построение профиля кулачка
- •4.4 Определение максимальной линейной скорости и ускорения конца толкателя
- •Заключение
- •Список литературы
3.3 Построение плана скоростей
Для
построения плана скоростей определяем
скорость точки, принадлежащей ведущему
звену. Принимаем
 .
.

Выбираем масштабный коэффициент построения плана скоростей:

3.4 Построение плана частот вращения
Для построения плана частот выбираем масштабный коэффициент

Из плана частот находим значение частот водила, солнечного колеса, сателлитов:




Найдем аналитически частоту выходного звена:



Найдем процент расхождения:


4 Синтез и анализ кулачкового механизма
Исходные данные:
а) диаграмма движения выходного звена
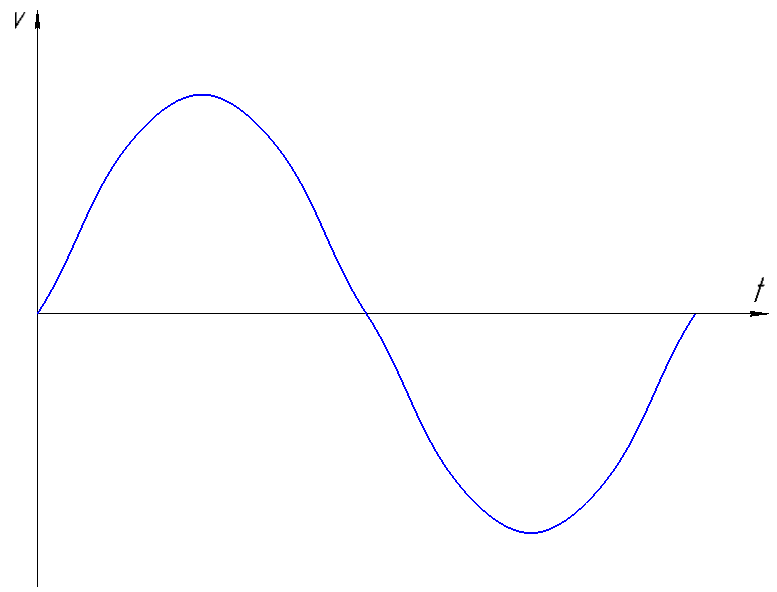
б) частота вращения кулачка nкул=2200мин-1;
в) ход толкателя h=9 мм;
г) допускаемый угол давления α=24 град;
д) рабочий угол кулачка φр=154 град;
е) кулачковый механизм с колебателем;
4.1 Построение кинематических диаграмм и определение масштабных коэффициентов
По заданному графику скорости толкателя v = f(t), графическим интегрированием по методу хорд и дифференцированием по методу хорд получаю графики ускорения и перемещения роликового толкателя. Графики a = f(v), a = f(s), v = f(s) получаем методом исключения общего переменного.
База интегрирования:

Масштабный коэффициент перемещения толкателя:

где ysmax–максимальное значение ординаты графика s=f(t), мм.
Масштабный коэффициент времени:

где
nкул–
частота вращения кулачка:

 =180
мм –
длина
отрезка на оси абсцисс графика,
изображающая время поворота кулачка
на рабочий угол.
=180
мм –
длина
отрезка на оси абсцисс графика,
изображающая время поворота кулачка
на рабочий угол.
Масштабный коэффициент скорости толкателя:

Масштабный коэффициент ускорения толкателя:

4.2 Определение минимального радиуса кулачка
Принимаю
масштабный коэффициент построения

По оси ординат графика v’ –s’в масштабе K’S откладываем величину перемещения толкателя y’Smax, мм:

Находим отрезки в масштабе K’S, изображающие перемещение толкателя в каждом положении графически.
Отрезки приведенной скорости толкателя определим графически, для чего находим максимальное значение приведенной скорости:

где yvmax – максимальное значение ординаты графика v = f(t), мм,
ωкул – угловая скорость кулачка,

Для остальных положений отрезки приведенной скорости определяются графически.
Значение минимального радиуса центрового профиля кулачка:

Радиус ролика:

Тогда истинное значение минимального радиуса кулачка:

4.3 Построение профиля кулачка
Строим
профиль кулачка в масштабе
 Проводим
из цента О1
окружность минимального радиуса Ro
и окружность
дезаксиала радиусом е.
Проводим
из цента О1
окружность минимального радиуса Ro
и окружность
дезаксиала радиусом е.
На
окружности минимального радиуса
 ,
в обращенном движении, откладываем
рабочий угол
,
в обращенном движении, откладываем
рабочий угол
![]() .
Через точки
деления 0, 1, 2, 3..., 8 проводим навстречу
выбранному направлению угловой скорости
кулачка касательные к окружности
дезаксиала,
на которых откладываем от окружности
минимального радиуса значения перемещения
толкателя, найденные в масштабе
.
Через точки
деления 0, 1, 2, 3..., 8 проводим навстречу
выбранному направлению угловой скорости
кулачка касательные к окружности
дезаксиала,
на которых откладываем от окружности
минимального радиуса значения перемещения
толкателя, найденные в масштабе
 .
Соединив концы этих отрезков плавной
кривой, получим центровой профиль
кулачка. Методом обкатки центрового
профиля
радиусом r
строим действительный профиль кулачка
и изображаем тип толкателя.
.
Соединив концы этих отрезков плавной
кривой, получим центровой профиль
кулачка. Методом обкатки центрового
профиля
радиусом r
строим действительный профиль кулачка
и изображаем тип толкателя.
4.4 Определение максимальной линейной скорости и ускорения конца толкателя
Определяют максимальную линейную скорость и ускорение следующим образом.
Для толкателя


где уvmax, уamax- максимальные ординаты скорости и ускорения на графиках v-t и a-t соответственно, мм.
 .
.
