
- •050708 (031200) Педагогика и методика начального образования дпп. Ф. 06. Математика
- •Глава I. Элементы логики
- •§ 1. Множества и операции над ними
- •1. Понятие множества и элемента множества
- •2. Способы задания множеств
- •3. Отношения между множествами. Подмножество. Равные множества. Универсальное множество. Круги Эйлера. Числовые множества.
- •4. Пересечение множеств
- •5. Объединение множеств
- •6. Свойства пересечения и объединения множеств
- •7. Вычитание множеств. Дополнение множества до универсального
- •8. Понятие разбиения множества на классы с помощью одного, двух, трех свойств
- •9. Декартово произведение множеств
- •10. Число элементов в объединении и разности конечных множеств
- •11. Число элементов в декартовом произведении конечных множеств
- •12. Основные понятия:
- •§ 2. Математические понятия
- •3. Способы определения понятий
- •4. Основные выводы
- •§ 3. Математические предложения
- •§ 4. Математическое доказательство
- •26. Схемы дедуктивных умозаключений.
- •§5. Текстовая задача и процесс ее решения
- •29. Структура текстовой задачи
- •30. Методы и способы решения текстовых задач
- •31. Этапы решения задачи и приемы их выполнения
- •2. Поиск и составление плана решения задачи
- •3. Осуществление плана решения задачи
- •4. Проверка решения задачи
- •5. Моделирование в процессе решения текстовых задач
- •Упражнения
- •32. Решение задач «на части»
- •Упражнения
- •33. Решение задач на движение
- •Упражнения
- •34. Основные выводы.
- •§6. Комбинаторные задачи и их решение
- •§ 7. Алгоритмы и их свойства
- •Упражнения
- •Упражнения
- •Глава II. Элементы алгебры
- •§ 8. Соответствия между двумя множествами
- •41. Понятие соответствия. Способы задания соответствий
- •2. Граф и график соответствия. Соответствие, обратное данному. Виды соответствий.
- •3. Взаимно-однозначные соответствия
- •Упражнения
- •42. Взаимно однозначные соответствия. Понятие взаимно однозначного отображения множества х на множество y
- •2. Равномощные множества. Способы установления равномощности множеств. Счетные и несчетные множества.
- •Упражнения
- •43. Основные выводы § 8
- •§ 9. Числовые функции
- •44. Понятие функции. Способы задания функций
- •2. График функции. Свойство монотонности функции
- •Упражнения
- •45. Прямая и обратная пропорциональности
- •Упражнения
- •46. Основные выводы § 9
- •§10. Отношения на множестве
- •47. Понятие отношения на множестве
- •Упражнения
- •48. Свойства отношений
- •R рефлексивно на х ↔ х r х для любого х € X.
- •R симметрично на х ↔ (х r y →yRx).
- •49. Отношения эквивалентности и порядка
- •Упражнения
- •50. Основные выводы § 10
- •§ 11. Алгебраические операции на множестве
- •51. Понятие алгебраической операции
- •Упражнения
- •52. Свойства алгебраических операций
- •Упражнения
- •53. Основные выводы § 11
- •§ 12. Выражения. Уравнения. Неравенства
- •54. Выражения и их тождественные преобразования
- •Упражнения
- •55. Числовые равенства и неравенства
- •Упражнения
- •56. Уравнения с одной переменной
- •2. Равносильные уравнения. Теоремы о равносильности уравнений
- •3. Решение уравнений с одной переменной
- •Упражнения
- •57. Неравенства с одной переменной
- •2. Равносильные неравенства. Теоремы о равносильности неравенств
- •3. Решение неравенств с одной переменной
- •Упражнения
- •58. Основные выводы § 12
- •Упражнения
- •Глава III. Натуральные числа и нуль
- •§ 13. Из истории возникновения понятия натурального числа
- •§ 14. Аксиоматическое построение системы натуральных чисел
- •59. Об аксиоматическом способе построения теории
- •Упражнения
- •60. Основные понятия и аксиомы. Определение натурального числа
- •Упражнения
- •61. Сложение
- •62. Умножение
- •63. Упорядоченность множества натуральных чисел
- •Упражнения
- •64. Вычитание
- •Упражнения
- •65. Деление
- •66. Множество целых неотрицательных чисел
- •Упражнения
- •67. Метод математической индукции
- •Упражнения
- •68. Количественные натуральные числа. Счет
- •Упражнения
- •69. Основные выводы § 14
- •70. Теоретико-множественный смысл натурального числа, нуля и отношения «меньше»
- •Упражнения
- •Лекция 36. Теоретико-множественный подход в построении множества целых неотрицательных чисел.
- •71. Теоретико-множественный смысл суммы
- •Упражнения
- •72. Теоретико-множественный смысл разности
- •Упражнения
- •73. Теоретико-множественный смысл произведения
- •Упражнения
- •74. Теоретико-множественный смысл частного натуральных чисел
- •Упражнения
- •75. Основные выводы § 15
- •§16. Натуральное число как мера величины
- •76. Понятие положительной скалярной величины и ее измерения
- •Упражнения
- •77. Смысл натурального числа, полученного в результате измерения величины. Смысл суммы и разности
- •Упражнения
- •78. Смысл произведения и частного натуральных чисел, полученных в результате измерения величин
- •79. Основные выводы § 16
- •80. Позиционные и непозиционные системы счисления
- •81. Запись числа в десятичной системе счисления
- •Упражнения
- •82. Алгоритм сложения
- •Упражнения
- •83. Алгоритм вычитания
- •Упражнения
- •84. Алгоритм умножения
- •Упражнения
- •85. Алгоритм деления
- •86. Позиционные системы счисления, отличные от десятичной
- •87. Основные выводы § 17
- •§ 18. Делимость натуральных чисел
- •88. Отношение делимости и его свойства
- •89. Признаки делимости
- •90. Наименьшее общее кратное и наибольший общий делитель
- •2. Основные свойства наименьшего общего кратного и наибольшего общего делителя чисел
- •3. Признак делимости на составное число
- •Упражнения
- •91. Простые числа
- •92. Способы нахождения наибольшего общего делителя и наименьшего общего кратного чисел
- •93. Основные выводы § 18
- •3. Дистрибутивности:
- •§ 19. О расширении множества натуральных чисел
- •94. Понятие дроби
- •Упражнения
- •95. Положительные рациональные числа
- •96. Множество положительных рациональных чисел как расширение
- •97. Запись положительных рациональных чисел в виде десятичных дробей
- •98. Действительные числа
- •99. Основные выводы § 19
- •Глава IV. Геометрические фигуры и величины
- •§ 20. Из истории возникновения и развития геометрии
- •1. Сущность аксиоматического метода в построении теории
- •2. Возникновение геометрии. Геометрия Евклида и геометрия Лобачевского
- •3. Система геометрических понятий, изучаемых в школе. Основные свойства принадлежности точек и прямых, взаимного расположения точек на плоскости и прямой.
- •§ 21. Свойства геометрических фигур на плоскости
- •§ 22. Построение геометрических фигур
- •1. Элементарные задачи на построение
- •2. Этапы решения задачи на построение
- •Упражнения
- •3. Методы решения задач на построение: преобразования геометрических фигур на плоскости: центральная, осевая симметрии, гомотетия, движение.
- •Основные выводы
- •§24. Изображение пространственных фигур на плоскости
- •1. Свойства параллельного проектирования
- •2. Многогранники и их изображение
- •Тетраэдр Куб Октаэдр
- •Упражнения
- •3. Шар, цилиндр, конус и их изображение
- •Основные выводы
- •§ 25. Геометрические величины
- •1. Длина отрезка и ее измерение
- •1) Равные отрезки имеют равные длины;
- •2) Если отрезок состоит из двух отрезков, то его длина равна сумме длин его частей.
- •Упражнения
- •2. Величина угла и ее измерение Каждый угол имеет величину. Специального названия для нее в
- •1) Равные углы имеют равные величины;
- •2) Если угол состоит из двух углов, то его величина равна сумме величин его частей.
- •Упражнения
- •1) Равные фигуры имеют равные площади;
- •2) Если фигура состоит из двух частей, то ее площадь равна сумме площадей этих частей.
- •4. Площадь многоугольника
- •5. Площадь произвольной плоской фигуры и ее измерение
- •Упражнения
- •Основные выводы
- •1. Понятие положительной скалярной величины и ее измерение
- •1) Масса одинакова у тел, уравновешивающих друг друга на весах;
- •2) Масса складывается, когда тела соединяются вместе: масса нескольких тел, взятых вместе, равна сумме их масс.
- •Заключение
- •Список литературы
§ 21. Свойства геометрических фигур на плоскости
Лекция 53. Свойства геометрических фигур на плоскости
План:
1. Геометрические фигуры на плоскости и их свойства
2. Углы, параллельные и перпендикулярные прямые
3. Параллельные и перпендикулярные прямые
Геометрическую фигуру определяют как любое множество точек. Отрезок, прямая, круг, шар – геометрические фигуры.
Если все точки геометрической фигуры принадлежат одной плоскости, она называется плоской. Например, отрезок, прямоугольник – это плоские фигуры. Существуют фигуры, не являющиеся плоскими. Это, например, куб, шар, пирамида.
Так как понятие геометрической фигуры определено через понятие множества, то можно говорить о том, что одна фигура включена в другую (или содержится в другой), можно рассматривать объединение, пересечение и разность фигур.
Например, объединением двух лучей АВ и МК является прямая КВ, а их пересечение есть отрезок АМ.
К А М В

Различают выпуклые и невыпуклые фигуры. Фигура называется выпуклой, если она вместе с любыми двумя своими точками содержит также соединяющий их отрезок.
Фигуры F₁ выпуклая, а фигура F₂ - невыпуклая.

F₁ F₂
Выпуклыми фигурами являются плоскость, прямая, луч, отрезок, точка, круг.
Для многоугольников известно другое определение: многоугольник называется выпуклым, если он лежит по одну сторону от каждой прямой, содержащей его сторону. Так как равносильность этого определения и данного выше для многоугольника доказана, то можно пользоваться и тем, и другим.
Рассмотрим некоторые понятия, изучаемые в школьном курсе геометрии, их определения и свойства, принимая их без доказательства.
Углы
Угол– это геометрическая фигура, которая состоит из точки и двух лучей, исходящих из этой точки. Лучи называются сторонами угла, а их общее начало – его вершиной.
Угол обозначают по-разному: указывают либо его вершину, либо его стороны, либо три точки: вершину и точки на сторонах угла: А,(k,l),АВС.
Угол называется развернутым, если его стороны лежат на одной прямой.
Угол, составляющий половину развернутого угла, называется прямым.Угол, меньший прямого, называетсяострым. Угол, больший прямого, но меньший развернутого, называетсятупым.
Плоский угол– это часть плоскости, ограниченная двумя различными лучами, исходящими из одной точки.
Существуют два плоских угла, образованных двумя лучами с общим началом. Они называются дополнительными.
А
О
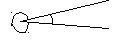
В
Углы, которые рассматриваются в планиметрии, не превосходят развернутого.
Два угла называются смежными, если у них одна сторона общая, а другие стороны этих углов являются дополнительными полупрямыми.
Сумма смежных углов равна 180º. Справедливость этого свойства вытекает их определения смежных углов.
Два угла называются вертикальными,если стороны одного угла являются дополнительными полупрямыми сторон другого.
Вертикальные углы равны.
Параллельные и перпендикулярные прямые
Две прямые на плоскости называются параллельными, если они не пересекаются
Если прямая aпараллельна прямойb, то пишутa║b.
Рассмотрим некоторые свойства параллельных прямых, и прежде всего признаки параллельности.
Признаками называют теоремы, в которых устанавливается наличие какого-либо свойства объекта, находящегося в определенной ситуации. В частности, необходимость рассмотрения признаков параллельности прямых вызвана тем, что нередко в практике требуется решить вопрос о взаимном расположении двух прямых, но в то же время нельзя непосредственно воспользоваться определением.
Рассмотрим следующие признаки параллельности прямых:
1. Две прямые, параллельные третьей, параллельны друг другу.
2. Если внутренние накрест лежащие углы равны или сумма внутренних односторонних углов равна 180º, то прямые параллельны.
Справедливо утверждение, обратноевторому признаку параллельности прямых: если две параллельные прямые пересечены третьей, то внутренние накрест лежащие углы равны, а сумма односторонних углов равна 180º.
Важное свойство параллельных прямых раскрываются в теореме,носящей имя древнегреческого математикаФалеса: если параллельные прямые, пересекающие стороны угла отсекают на одной его стороне равные отрезки, то они отсекают равные отрезки и на другой его стороне.
Две прямые называются перпендикулярными, если они пересекаются под прямым углом.
Если прямая а перпендикулярна прямой b, то пишутab.
Основные свойства перпендикулярных прямых нашли отражение в двух теоремах:
1. Через каждую точку прямой можно провести перпендикулярную к ней прямую, и только одну.
2. Из любой точки, не лежащей на данной прямой, можно опустить на эту прямую перпендикуляр, и только один.
Перпендикуляром к данной прямой называется отрезок прямой, перпендикулярной данной, имеющей концом их точку пересечения. Конец этого отрезка называется основанием перпендикуляра.
Длина перпендикуляра, опущенного из данной точки на прямую, называется расстоянием от точки до прямой.
Расстоянием между параллельными прямыминазывается расстояние от какой-нибудь точки одной прямой до другой.
Лекция 54. Свойства геометрических фигур на плоскости
План:
4. Треугольники, четырехугольники, многоугольники. Формулы площадей треугольника, прямоугольника, параллелограмма, трапеции.
5. Окружность, круг.
Треугольники
Треугольник – одна из простейших геометрических фигур. Но его изучение породило целую науку – тригонометрию, которая возникла из практических потребностей при измерении земельных участков, составлении карт местности, конструировании различных механизмов.
Треугольником называется геометрическая фигура, которая состоит из трех точек, не лежащих на одной прямой, и трех попарно соединяющих их отрезков.
Любой треугольник разделяет плоскость на две части: внутреннюю и внешнюю. Фигуру, состоящую из треугольника и его внутренней области, также называют треугольником ( или плоским треугольником).
В любом треугольнике выделяют следующие элементы: стороны, углы, высоты, биссектрисы, медианы, средние линии.
Углом треугольника АВС при вершине А называется угол, образованный полупрямыми АВ и АС.
Высотой треугольника, опущенной из данной вершины, называется перпендикуляр, проведенный из этой вершины к прямой, содержащей противоположную сторону.
Биссектрисойтреугольника называется отрезок биссектрисы угла треугольника, соединяющей вершину с точкой на противоположной стороне.
Медианойтреугольника, проведенной из данной вершины, называется отрезок, соединяющий эту вершину с серединой противолежащей стороны.
Средней линиейтреугольника называется отрезок, соединяющий середины двух его сторон.
Треугольники называются равными, если у них соответствующие стороны и соответствующие углы равны. При этом соответствующие углы должны лежать против соответствующих сторон.
На практике и в теоретических построениях часто пользуются признаками равенства треугольников, обеспечивающих более быстрое решение вопроса об отношениях ме5жду ними. Таких признаков три:
1. Если две стороны и угол между ними одного треугольника равны соответственно двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
2. Если сторона и прилежащие к ней углы одного треугольника равны соответственно стороне и прилежащим к ней углам другого треугольника, то такие треугольники равны.
3. Если три стороны одного треугольника равны соответственно трем сторонам другого треугольника, то такие треугольники равны.
Треугольник называется равнобедренным, если у него две стороны равны. Эти равные стороны называются боковыми, а третья сторона называется основанием треугольника.
Равнобедренные треугольники обладают рядом свойств, например:
В равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой.
Отметим несколько свойств треугольников.
1. Сумма углов треугольника равна 180º.
Из этого свойства следует, что в любом треугольнике хотя бы два угла острые.
2. Средняя линия треугольника, соединяющая середины двух сторон, параллельна третьей стороне и равна ее половине.
3. В любом треугольнике каждая сторона меньше суммы двух других сторон.
Для прямоугольного треугольника верна теорема Пифагора: квадрат гипотенузы равен сумме квадратов катетов.
Четырехугольники
Четырехугольникомназывается фигура, которая состоит из четырех точек и четырех последовательно соединяющих их отрезков, причем никакие три из данных точек не должны лежать на одной прямой, а соединяющие их отрезки не должны пересекаться. Данные точки называются вершинами четырехугольника, а соединяющие их отрезки – его сторонами.
Любой четырехугольник разделяет плоскость на две части: внутреннюю и внешнюю. Фигуру, состоящую из четырехугольника и его внутренней области, также называется четырехугольником (или плоским четырехугольником).
Вершины четырехугольника называют соседними, если они являются концами одной из его сторон. Вершины, не являющиеся соседними, называются противолежащими. Отрезки, соединяющие противолежащие вершины четырехугольника, называются диагоналями.
Стороны четырехугольника, исходящие из одной вершины, называются соседними. Стороны, не имеющие общего конца, называются противолежащими. У четырехугольника АВСDвершины А и В – противолежащие, стороны АВ и ВС – соседние, ВС и АD– противолежащие; отрезки АС и ВD– диагонали данного четырехугольника.
В С Р М Т

А DК
Четырехугольники бывают выпуклые и невыпуклые. Так, четырехугольник АВСD– выпуклый, а четырехугольник КРМТ – невыпуклый. Среди выпуклых четырехугольников выделяют параллелограммы и трапеции.
Параллелограммом называется четырехугольник, у которого противолежащие стороны параллельны.
Пусть АВСD– параллелограмм. Из вершины В на прямую АDопустим перпендикуляр ВЕ. Тогда отрезок ВЕ называется высотой параллелограмма, соответствующей сторонам ВС и АD. Отрезок
М

А Е D
СМ – высота параллелограмм, соответствующая сторонам СDи АВ.
Чтобы упростить распознавание параллелограммов, рассматривают следующий признак: если диагонали четырехугольника пересекаются и точкой пересечения делятся пополам, то данный четырехугольник – параллелограмм.
Ряд свойств параллелограмма, которые не содержатся в его определении, формулируют в виде теорем и доказывают. Среди них:
1. Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам.
2. У параллелограмма противолежащие стороны и противолежащие углы равны.
Рассмотрим теперь определение трапеции и ее основное свойство.
Трапецией называется четырехугольник, у которого только две противолежащие стороны параллельны.
Эти параллельные стороны называются основаниями трапеции. Две другие стороны называются боковыми.
Отрезок, соединяющий середины боковых сторон, называется средней линией трапеции.
Средняя линия трапеции обладает свойством: она параллельна основаниям и равна их полусумме.
Из множества параллелограммов выделяют прямоугольники и ромбы.
Прямоугольникомназывается параллелограмм, у которого все углы прямые.
Исходя из этого определения, можно доказать, что диагонали прямоугольника равны.
Ромбомназывается параллелограмм, у которого все стороны равны.
Пользуясь этим определением, можно доказать, что диагонали ромба пересекаются под прямым углом и являются биссектрисами его углов.
Из множества прямоугольников выделяют квадраты.
Квадратом называют прямоугольник, у которого все стороны равны.
Так как стороны квадрата равны, то он является также ромбом. Следовательно, квадрат обладает свойствами прямоугольника и ромба.
Многоугольники
Обобщением понятия треугольника и четырехугольника является понятие многоугольника. Определяется оно через понятие ломаной.
Ломаной А₁А₂А₃…Аnназывается фигура, которая состоит из точек А₁, А₂, А₃, …, Аnи соединяющих их отрезков А₁А₂, А₂А₃, …, Аn-₁Аn. Точки А₁, А₂, А₃, …, Аnназываются вершинами ломаной, а отрезки А₁А₂, А₂А₃, …, Аn-₁Аn– ее звеньями.
Если ломаная не имеет самопересечений, то она называется простой. Если ее концы совпадают, то она называется замкнутой. О ломаных, изображенных на рисунке можно сказать: а) – простая; б) – простая замкнутая; в) – замкнутая ломаная, не являющаяся простой.
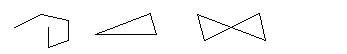
а) б) в)
Длиной ломаной называется сумма длин ее звеньев.
Известно, что длина ломаной не меньше длины отрезка, соединяющего ее концы.
Многоугольником называется простая замкнутая ломаная, если ее соседние звенья не лежат на одной прямой.
Вершины ломаной называют вершинами многоугольника, а ее звенья – его сторонами. Отрезки, соединяющие несоседние вершины, называются диагоналями.
Любой многоугольник разделяет плоскость на две части, одна из которых называется внутренней, а другая – внешней областью многоугольника (или плоским многоугольником).
Различают выпуклые и невыпуклые многоугольники.
Выпуклый многоугольник называется правильным, если у него все стороны и все углы равны.
Правильным является равносторонний треугольник, правильным четырехугольником – квадрат.
Углом выпуклого многоугольника при данной вершине называется угол, образуемый его сторонами, сходящимися в этой вершине.
Известно, что сумма углов выпуклого n-угольника равна 180º•(n– 2).
В геометрии, кроме выпуклых и невыпуклых многоугольников, рассматривают еще многоугольные фигуры.
Многоугольной фигурой называется объединение конечного множества многоугольников.
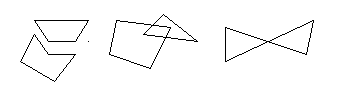
а) б) в)
Многоугольники, из которых состоит многоугольная фигура, могут не иметь общих внутренних точек, могут иметь общие внутренние точки.
Говорят, что многоугольная фигура Fсостоит из многоугольных фигур, если она является их объединением, а сами фигуры не имеют общих внутренних точек. Например, о многоугольных фигурах, изображенных на рисунке а) и в), можно сказать, что они состоят из двух многоугольных фигур или что они разбиты на две многоугольные фигуры.
Окружность и круг
Окружностьюназывается фигура, которая состоит из всех точек плоскости, равноудаленных от данной точки, называемойцентром.
Любой отрезок, соединяющий точку окружности с ее центром, называется радиусом окружности. Радиусомназывается также расстояние от любой точки окружности до ее центра.
Отрезок, соединяющий две точки окружности, называется хордой. Хорда, проходящая через центр, называетсядиаметром.
Кругом называется фигура, которая состоит из всех точек плоскости, находящихся на расстоянии, не большем данного, от данной точки. Эта точка называется центром круга, а данное расстояние – радиусом круга.
Границей круга является окружность с теми же центром и радиусом.
Напомним некоторые свойства окружности и круга.
Говорят, что прямая и окружность касаются, если они имеют единственную общую точку. Такую прямую называют касательной, а общую точку прямой и окружности – точкой касания. Доказано, что если прямая касается окружности, то она перпендикулярна радиусу, проведенному в точку касания. Справедливо и обратное утверждение (рис. а).
Центральным углом в окружности называется плоский угол с вершиной в ее центре. Часть окружности, расположенная внутри плоского угла, называется дугой окружности, соответствующей этому центральному углу (рис.б).
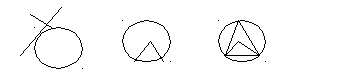
а) б) в)
Угол, вершина которого лежит на окружности, а стороны пересекают ее, называется вписанным в эту окружность (рис.в).
Угол, вписанный в окружность, обладает следующим свойством: он равен половине соответствующего центрального угла. В частности, углы, опирающиеся на диаметр – прямые.
Окружность называется описанной около треугольника, если она проходит через все его вершины.
Чтобы описать окружность около треугольника, надо найти ее центр. Правило его нахождения обосновывается следующей теоремой:
Центр окружности, описанной около треугольника, является точкой пересечения перпендикуляров к его сторонам, проведенных через середины этих сторон (рис.а).

а) б)
Окружность называется вписанной в треугольник, если она касается всех его сторон.
Правило нахождения центра такой окружности обосновывается теоремой:
Центр окружности, вписанной в треугольник, является точкой пересечения его биссектрис (рис.б)
Таким образом, серединные перпендикуляры и биссектрисы пересекаются в одной точке соответственно. В геометрии доказано, что медианы треугольника пересекаются в одной точке. Эту точку называют центром тяжести треугольника, а точку пересечения высот – ортоцентром.
Таким образом, во всяком треугольнике существует четыре замечательные точки: центр тяжести, центры вписанной и описанной окружностей и ортоцентр.
Около всякого правильного многоугольника можно описать окружность и во всякий правильный многоугольник можно вписать окружность, причем центры описанной и вписанной окружностей совпадают.
