10. Число элементов в объединении и разности конечных множеств

Нам известно, как находят объединение двух конечных непересекающихся множеств. Например, если А = {х, у, z}, а В = {k,l,m,p}, то А∪В ={х, у,z,k,l,m,p}. Чтобы ответить на вопрос: «Сколько элементов в полученном множестве?», достаточно пересчитать их.

А как определить число элементов в объединении конечных множеств, не образуя его и не обращаясь к пересчету элементов?

Условимся предложение «Множество А содержит а элементов» записывать в таком виде: n(А) = а. Например, если А = {х, у,z}, то утверждение «Множество А содержит три элемента можно записать так:n(А) = 3.

Можно доказать, что в множестве А содержится а элементов, а в множестве В – bэлементов и множества А и В не пересекаются, то в объединении множеств А и В содержится а +bэлементов, т.е.

n(А∪В) = n(А) + n(В) = в + b.(1)

Это правило нахождения числа элементов в объединении двух конечных непересекающихся множеств, его можно обобщить на случай tпопарно непересекающихся множеств, т.е. если множества А₁, А₂, …, Аtпопарно не пересекаются, тоn(А₁ ∪ А₂ ∪ …∪ Аt) =n(А₁) + n(А₂) + … + n(Аt).

Для выше описанных множеств n(А) = 3,n(В) = 4. Видим, что А∩ В =∅. Тогдаn(А∪В) =n(А) +n(В) = 3 + 4 = 7.

Нетрудно убедиться в том, что если В ⊂ А, то n (В´А) = n(А) - n(В),т.е. число элементов дополнения подмножества В до конечного множества А равно разности численностей этих множеств.

Пусть, например, А = {х, у, z,p,t}, а В = { х,p,t}. Получаемn(А) = 5,n(В) = 3. Тогдаn(В´А) =n(А) -n(В) = 5 – 3 = 2.

Формула (1) позволяет находить число элементов в объединении конечных непересекающихся множеств. А если множества А и В имеют общие элементы, то как найти число элементов в их объединении?

Пусть, например, А = {х, у, z}, а В = {х,z, р,s,k}. Тогда А∪ В = {х, у,z, р,s,k}, т.е.n(А) = 3,n(В) = 5, аn(А∩ В) = 2 и, значит, общие элементы множеств А и В в объединении этих множеств записаны только один раз.

В общем виде правило подсчета элементов в объединении двух конечных множеств может быть представлено в виде формулы:

n(А∪В) = n(А) + n(В) - n(А ∩ В).(2)

Полученные формулы для подсчета числа элементов в объединении двух и более множеств можно использовать для решения текстовых задач следующего вида.

Задача. Из 40 студентов курса 32 изучают английский язык, 21 – немецкий язык, а 15 – английский и немецкий языки. Сколько студентов курса не изучает ни английский, ни немецкий языки?

Решение. Пусть А – множество студентов курса, изучающих английский язык, В – множество студентов курса, изучающих немецкий язык, С – множество всех студентов курса. По условию задачи: n(А) = 32,n(В) = 21,n(А∩ В) = 15,n(С) = 40. Требуется найти число студентов курса, не изучающих ни английского, ни немецкого языка.

1 способ.

1) Найдем число элементов в объединении данных множеств А и В. Для этого воспользуемся формулой (2):

n(А∪В) =n(А) +n(В) -n(А∩ В) = 32 + 21 – 15 = 38.

2) Найдем число студентов курса, которые не изучают ни английский, ни немецкий языки: 40 – 38 = 2.

2 способ.

1) Изобразим данные множества при помощи кругов Эйлера и определим число элементов в каждом из непересекающихся подмножеств (рисунок).

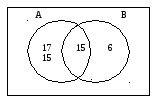
Так как в пересечении множеств А и В содержится 15 элементов, то студентов, изучающих только английский язык, будет 32 – 15 = 17, а студентов, изучающих только немецкий язык, 21 – 15 = 6. Тогда n(А∪В) = 17 + 15 + 6 = 38, и, следовательно, число студентов курса, которые не изучают ни английский, ни немецкий языки, будет 40 – 38 = 2.