Решение оптимизационных задач. Алгоритм Дейкстры.

Алгоритм Дейкстры — алгоритм на графах, изобретённый нидерландским ученым Э. Дейкстрой в 1959 году. Находит кратчайшее расстояние от одной из вершин графа до всех остальных. Алгоритм работает только для графов без рёбер отрицательного веса. Алгоритм широко применяется в программировании и технологиях, например, его используют протоколы маршрутизации OSPF и IS-IS.

Алгоритм Дейкстры решает задачу о кратчайших путях из одной вершины для взвешенного ориентированного графа G = (V, E) с исходной вершиной s, в котором веса всех рёбер неотрицательны ((u, v) ≥ 0 для всех (u, v)E).

Пример решения задачи. Поиск ведется на данном графе (Рис 3.1). Веса соответствуют длине ребер.

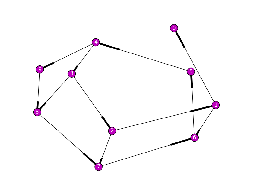Рис 3.1

Листинг 2.

import networkx as nx

import matplotlib.pyplot as plt

G = nx.DiGraph() #Объявляем орграф G

G.add_nodes_from(range(1, 7)) #Добавляем вершины из набора чисел(1..7)

for i in range(1,10):

G.add_edge(i, i-1) #Добавляем ребро, соединяющее вершину i с i-1

for i in range(1,10):

if(i+5<10):

G.add_edge(i, i+5, weight = i*0.5+2)#Устанавливаем веса на ребра

nx.draw(G, node_color = 'm', font_color = 'w')

plt.show()

print(nx.dijkstra_path(G, 2, 8)) #Поиск и вывод массива вершин

# Использование функции для нахождения маршрута. Поиск начинается с вершины 2 и идет до вершины 8.

Выходные данные:

[2, 1, 6, 5, 4, 3, 8]

Алгоритм поиска.

0. G – данный ориентированный граф с взвешенными ребрами. Требуется найти кратчайшие пути из вершины s во все остальные вершины графа G.

1. (Начало). Положить label(s) = 0, perm(s) = 1 и pred(s) = s. Для всех v <> s положить label(v) = ∞, perm(v) = 0, pred(v) = v.

2. Пусть i = 0 и u = s. (u – последняя из вершин с неизменной меткой. Теперь – это вершина s.)

3. (Вычисление label и изменение элементов массива pred). Положить i = i + 1. Выполнить для каждой вершины, кроме вершин с неизменной меткой, следующие действия: 1) Положить M = min{label(v), label(u) + w(u, v)}. 2) Если M<label(v), то положить label(v) = M и pred(v) = u.

4. (Выделение вершин u_i.) Среди всех вершин, которые не помечены неизменной меткой, найти вершину w с наименьшей меткой. (Если таких вершин несколько, то выбор можно сделать произвольно.) Положить perm(w) = 1 и u_i = w (u_i = w, и она является последней вершиной с неизменной меткой.)

5. Если i < n – 1, то идти к шагу 3. Иначе halt. (Все кратчайшие пути найдены). Метки вершин представляют собой длины кратчайших путей. v, pred(v), pred(pred(v)), …, s есть вершины кратчайшего ориентированного s-v – пути.

Здесь label - это массив, в котором хранятся текущие метки вершин. Вершины становятся постоянно помеченными, когда они оказываются равными u_i для какого-либо i. Мы используем массив perm, чтобы указать, какие вершины постоянно помечены. Если perm(v) = 1, то v является постоянно помеченной вершиной. Отметим, что в таком случае метка v равна d(s, v). Вначале perm(s) = 1 и perm(v) = 0 для всех v<>s.

Pred – массив указателей на вершины, из которых осуществлен переход в вершины с неизменной меткой, то v, pred(v), pred(pred(v)), …, s есть вершины, составляющие кратчайший ориентированный путь из s в v.

Данный алгоритм работает также для решения задачи коммивояжера.